Тема 1: элементы теории множеств и комбинаторики
Обозначим |A| - количество элементов множества А. Число элементов пустого множества равно нулю: |Ø|=0. Число элементов множества, образованного единственным элементом, равно единице: |A|=1. Важную роль в комбинаторике играют следующие правила:
Правило сложения: для любых множеств 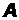 иВ таких, что
иВ таких, что 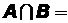 Øверно:|A+B|=|A|+|B|.
Øверно:|A+B|=|A|+|B|.
Правило умножения: Для любых конечных множеств Аи В: |A 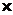 B|=|A|·|B|.
B|=|A|·|B|.
На практике это означает, что если первый элементавыбирается из nвозможных, а второй элемент b - из kвозможных, то число упорядоченных пар вида (a,b) равно произведению n·k.
Правило вычитания: Для каждой частиАконечного множества Вверно: |A-B|=|A|-|B|.
Правило объединения: Для любых конечных множествАи Вверно:
|A 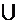 B|=|A|+|B|-|A
B|=|A|+|B|-|A 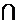 B|.
B|.
Правило объединения для трех множеств:
|A 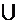 B
B 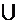 C|=|A|+|B|+|C|-|A
C|=|A|+|B|+|C|-|A 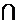 B|-|B
B|-|B 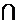 C|-|A
C|-|A 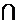 C|+|A
C|+|A 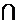 B
B 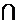 C|.
C|.
Перестановкамиизnэлементовназывают всевозможные n–расстановки, каждая из которых содержит все эти элементы по одному разу и которые отличаются друг от друга лишь порядком элементов.
Число n–перестановок обозначают через 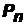 . Чтобы узнать, сколько перестановок можно составить из n элементов, надо перемножить все натуральные числа от 1 до n. Это произведение обозначают n! (читается n-факториал):
. Чтобы узнать, сколько перестановок можно составить из n элементов, надо перемножить все натуральные числа от 1 до n. Это произведение обозначают n! (читается n-факториал): 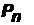 = 1·2·3·
= 1·2·3· 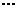 ·
· 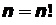
В частности, если n=0, то полагают 0!=1.
Пусть конечное множествоАсодержит n элементов. ЧастьВмножества А, составленную из mэлементов, будем называть выборкой (без возвращения) mиз nэлементов множества А. Число всех таких выборок определяется числами m, nи обозначается символом 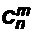 . Вместо слова выборка говорят также сочетание: m-сочетаниями из n элементовназывают всевозможные m-расстановки, составленные из этих элементов и отличающиеся друг от друга составом, но не порядком элементов. Число таких сочетаний вычисляется по формуле:
. Вместо слова выборка говорят также сочетание: m-сочетаниями из n элементовназывают всевозможные m-расстановки, составленные из этих элементов и отличающиеся друг от друга составом, но не порядком элементов. Число таких сочетаний вычисляется по формуле:
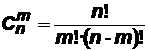 .
.
Числа 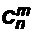 обладают следующими свойствами:
обладают следующими свойствами:
1) 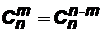 ;
;
2) 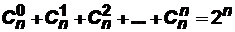 ;
;
3) для любого m, удовлетворяющего условию 1≤m≤n, справедливо равенство: 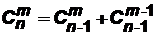 .
.
4) 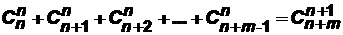 .
.
Классической задачей комбинаторики является также задача о числеразмещений: сколько существует способов, чтобы выбрать m из n различных элементов и разместить их по m различным местам? Число размещений m элементов из n обозначается 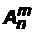 . Так как сначала мы выбираем m из n элементов, а затем упорядочиваем их, то для определения числа размещений надо перемножить число сочетаний
. Так как сначала мы выбираем m из n элементов, а затем упорядочиваем их, то для определения числа размещений надо перемножить число сочетаний 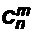 на число перестановок
на число перестановок 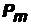 :
:
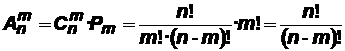 .
.
Если из конечного множества A, содержащего n элементов, mраз выбирать по одному элементу, каждый раз возвращая его обратно, то получим множество из mэлементов, которое называют выборкой с повторениямиили размещением с повторениями.
Число всех размещений с повторениями из n элементов по m зависит, очевидно, только от n и m (а не от природы множества A). Обозначим это число 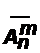 . Из правила произведения следует, что это число равно:
. Из правила произведения следует, что это число равно: 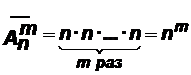 .
.
Если в перестановках из общего числа n элементов есть k различных элементов, при этом 1-й элемент повторяется 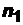 раз, 2-й элемент -
раз, 2-й элемент - 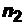 раз, k-й элемент -
раз, k-й элемент - 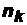 раз, причем
раз, причем 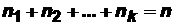 , то такие перестановки называют перестановками с повторениями изnэлементов. Число перестановок с повторениями из n элементов равно:
, то такие перестановки называют перестановками с повторениями изnэлементов. Число перестановок с повторениями из n элементов равно:
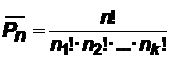 .
.
Пусть множество A содержит n•m элементов, среди которых по m одинаковых элементов каждого из n различных типов. Число способов выбрать m элементов из множества A называется выборкой с повторениями (или сочетаниями с повторениями) и вычисляется по формуле:
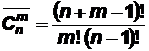
Задачи для самостоятельного решения:
1.1Из пунктаА в пункт В можно добраться самолетом, поездом, автобусом, а из него в пункт С – пешком, на тракторе, на лошади, на лодке. Сколькими способами можно выбрать дорогу от пунктаА до пункта С через В?
1.2Сколько существует пятизначных чисел, состоящих из цифр 1, 2 и 9, в которых цифра 1 повторяется 1 раз, а цифры 2 и 9 – по 2 раза?
