Математическое ожидание числа появления события в схеме независимых испытаний.

Пусть производится n независимых опытов, ве­роятность появления события в каждом из которых равна Р. Число появлений события в этих n опытах является случайной величиною Х распределённой по биномиальному закону. Однако, непосредственное вычисление её среднего значения громоздко. Для упрощения воспользуемся разложением, которым будем пользоваться в дальнейшем неоднократно: Число появления события в n опытах состоит из числа появлений события в отдельных опытах, т.е.

Где имеет закон распределения (принимает значение 1, если событие в данном опыте произошло, и значение 0, если событие в данном опыте не появилось).

Р	1-р	р

Поэтому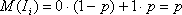

Или

т.е. среднее число появлений события в n независимых опытах равно произведению числа опытов на вероятность появления события в одном опыте.

Например, если вероятность попадания в цель при одном выстреле равна 0,1, то среднее число попадания в 20 выстрелах равно 20×0,1=2.

Дисперсия ДСВ

Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

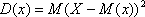
Для вычисления дисперсии можно использовать слегка преобразованную формулу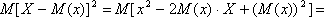

т.к. М(х), 2 и 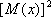постоянные величины, то

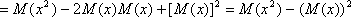
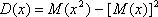
Свойства дисперсии

Свойство 1. Дисперсия постоянной равна нулю. По определению

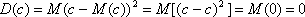
Свойство 2. Постоянную можно выносить за знак дисперсии с возведением в квадрат.

Доказательство: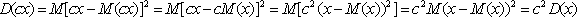

Центрированной случайной величиной называется отклонение случайной величины от ее математического ожидания.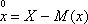

Центрированная величина обладает двумя удобными для преобразования свойствами: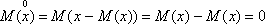

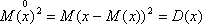
Свойство 3. Если случайные величины Х и У независимы, то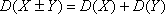

Дисперсия числа появления события в схеме независимых испытаний

Производится n независимых испытаний и вероятность появления события в каждом испытании равна р. Выразим, как и прежде, число появления события Х через число появления события в отдельных опытах

Так как опыты независимы, то и связанные с опытами случайные величины независимы. А в силу независимости имеем

Р	1-р	р

Но каждая из случайных величин имеет закон распределения и , поэтому по определению дисперсии

Где q=1-p

В итоге имеем ,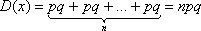

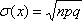
Среднее квадратическое отклонение

Дисперсия, как характеристика разброса случайной величины, имеет один недостаток. Если, например, Х – ошибка измерения имеет размерность ММ, то дисперсия имеет размерность . Поэтому часто предпочитают пользоваться другой характеристикой разброса – средним квадратическим отклонением, которое равно корню квадратному из дисперсии.

Среднее квадратическое отклонение имеет ту же размерность, что и сама случайная величина.