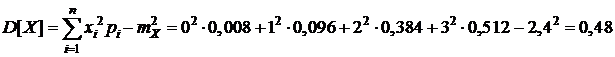Задача 5. Дискретная случайная величина

Условия вариантов задачи

В задачах 5.1-5.40 дискретная случайная величина Х может принимать одно из пяти фиксированных значений x1, x2, x3, x4, x5 с вероятностями p1, p2, p3, p4, p5 соответственно (конкретные значения приведены в таб. 5.1). Найти p отмеченные *. Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.

Таблица. 5.1

Вариант	x1	x2	x3	x4	x5	p1	p2	p3	p4	p5
5.1						0,2	0,2	0,2	0,2	0,2
5.2						0,1	0,2	0,3	0,2	0,2
5.3						0,4	0,1	0,1	0,3	0,1
5.4						0,3	0,3	0,1	0,1	0,2
5.5	-2	-1				0,2	0,2	0,2	0,2	0,2
5.6	-2	-1				0,1	0,3	0,2	0,2	0,2
5.7	-5	-2				0,5	0,1	0,1	0,2	0,1
5.8	-5	-2				0,1	0,2	0,1	0,3	0,3
5.9						0,2	0,2	0,2	0,2	0,2
5.10						0,3	0,2	0,1	0,2	0,2
5.11						0,1	0,2	0,3	0,4
5.12	-1					0,6	0,1	0,1	0,1	0,1
5.13	-1					0,3	0,2	0,1	0,1	0,3
5.14						0,1	0,2	0,3	0,4
5.15						0,5	0,1	0,1	0,1	0,2
5.16	-5	-4	-3			0,1	0,3	0,2	0,2	0,2
5.17	-2					0,3	0,2	0,1	0,1	0,3
5.18	-2					0,3	0,1	0,1	0,2	0,3
5.19	-2					0,15	0,15	0,2	0,4	0,1
5.20						0,1	0,1	0,1	0,1	0,6
5.21						0,3	0,15	0,25	0,15	0,15
5.22						0,2	0,2	0,2	0,2	0,2
5.23	-10	-4				0,2	0,2	0,2	0,2	0,2
5.24	-10	-4				0,3	0,1	0,2	0,1	0,3
5.25						0,1	0,2	0,3	0,35	0,05
5.26						0,7	0,1	0,1	0,05	0,05
5.27						0,2	0,3	0,05	0,25	0,2
5.28						0,6	0,1	0,1	0,05	0,15
5.29						0,3	0,3	0,1	0,15	0,15
5.30						0,05	0,15	0,2	0,4	0,2
5.31						0,1	0,3	0,4	0,1	*
5.32	-2	-1				0,5	0,1	*	0,1	0,2
5.33	-4	-3	-1			0,2	*	0,2	0,1	0,4
5.34	-6	-3	-1			*	0,1	0,1	0,1	0,1
5.35						0,3	*	0,3	0,1	0,1
5.36						0,2	0,2	*	0,2	0,2
5.37						0,2	0,3	0,1	*	0,2
5.38	-1					0,1	0,5	0,1	*	0,1
5.39	-4	-2				0,4	0,1	*	0,1	0,1
5.40	-1					*	0,3	0,1	0,3	0,1

Методические указания

Случайная величина (СВ) – это величина, которая в результате опыта со случайным исходом принимает то или иное значение, причем заранее до опыта неизвестно, какое именно. Обозначения случайной величины: X, Y; а их значения: x, y.

Случайная величина Х называется дискретной, если ее множество возможных значений W_X – счетное, т.е. элементы множества можно расположить в определенном порядке и пронумеровать.

Закон распределения случайной величины — любое правило, устанавливающее соответствие между значениями случайной величины и вероятностями ее наступления.

Рядом распределения дискретной СВ X называется таблица, в верхней строке которой перечислены все возможные значения СВ 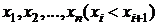, а в нижней — вероятности их появления 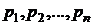, где :

			...
			...

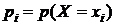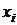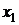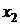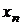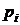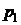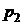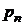Так как события 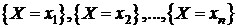несовместны и образуют полную группу, то справедливо контрольное соотношение

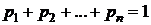. (5.1)

Функцией распределения случайной величины X называется вероятность того, что она примет значение меньшее, чем аргумент x функции F(x): .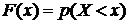

Свойства функции распределения:

1. F(- ) = 0 и F(+ ) = 1.

2. Неубывающая функция: .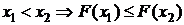

4. Вероятность попадания значения СВ X в интервал :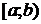

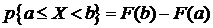(5.2)

Функция распределения дискретной СВ определяется так:

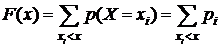(5.3)

где 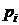– вероятности ряд распределения этой СВ.

Здесь суммируются вероятности всех тех значений 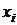, которые по своей величине меньше, чем x – аргумент функции F(x).

				...
				...

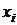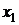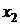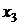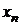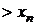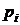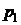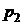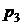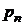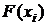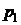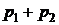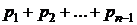Функция распределения любой дискретной СВ есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины, и равны вероятностям этих значений.

Математическое ожидание характеризует среднее значение случайной величины и для дискретной СВ определяется по формуле

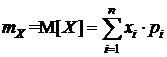(5.4)

Как видно из (5.4), в качестве математического ожидания СВ используется «среднее взвешенное значение», причем каждое из значений случайной величины учитывается с «весом», пропорциональным вероятности этого значения.

Дисперсияслучайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания и для дискретной СВ определяется по формуле:

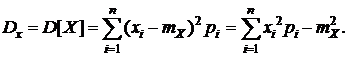(5.5)

Примеры

Пример 5.1. По командному пункту противника производится пуск трех ракет, причем вероятность попадания в цель при пуске одной ракеты равна 0,8. Построить ряд распределения числа попаданий.

Решение. Определим случайную величину X как число попаданий в цель при трех пусках ракет. Эта случайная величина может принимать следующие значения: 0, 1, 2, 3. Найдем вероятность принятия величиной X этих значений, используя формулу Бернулли:

,

,

,

.

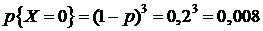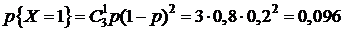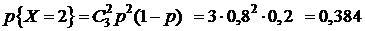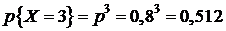Ряд распределения имеет следующий вид

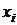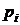	0,008	0,096	0,384	0,512

Как видим, условие (5.1) выполняется.

Пример 5.2. Зная ряд распределения для случайной величина X , описанной в примере 5.1, построить график функции распределения. Найти математическое ожидание и дисперсию дискретной случайной величины X.

Решение. Рассчитаем значения функции распределения для фиксированных значений 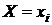, взятых из ряда распределения (пример 5.1).

1. .

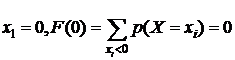2.

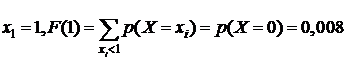
3. .

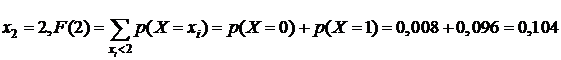4.

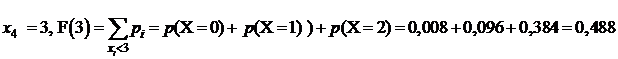
5. При 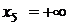, согласно свойствам функции распределения,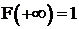

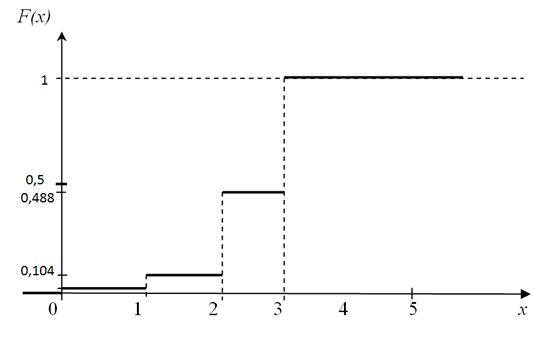
Рис. 5.1

Опишем построение графика функции распределения F(x) (рис. 5.1). Рассмотрим первый промежуток по оси Х от 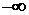до 0; согласно пункту 1 значение 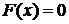и линия идет по оси Х до нуля включительно. Второй промежуток по оси Х от 0 до 1; согласно пункту 2 значение 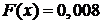значит проводим ступеньку высотой 0,008. Третий промежуток от 1 до 2; согласно пункту 3 значение 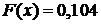значит проводим ступеньку высотой 0,104. Четвертый промежуток от 2 до 3; согласно пункту 4 значение 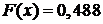значит проводим ступеньку высотой 0,488. Пятый промежуток от 3 до 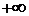; согласно пункту 5 значение 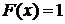значит проводим ступеньку высотой 1.

Математическое ожидание дискретной СВ X определим по формуле (5.4):

,

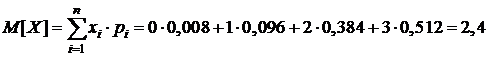Дисперсию дискретной СВ X определим по формуле (5.5):