Разработка алгоритма умножения.
РАЗРАБОТКА АЛГОРИТМА УМНОЖЕНИЯ.
1. Перевод сомножителей из десятичной системы счисления в четвертичную:
Множимое:
18| 4 0,72 Мн4 =102,2324
16 4| 4 4
2 0| 1 2,88
4 в соответствии с заданной кодировкой множимого
3,52 Мн2/4 =010010,101110
4
2,08
4
0,32
Множитель:
62| 4 в соответствии с заданной кодировкой множимого
60|15| 4
2 12 3 Мт4 =332,022
3 Мт2/4 =111110,001010
0,17
4
0,68
4
2,72
4
2,88
2. Запишем сомножители в форме с плавающей запятой в прямом (дополнительном) коде (т.к. алгоритм В):
Мн =0,00010010101110 Рмн= 0.0100 +0310 - закодировано по заданию
Мт =0,00111110001010 Рмт = 0.0100 +0410 - закодировано традиционно
3. Умножение двух чисел с плавающей запятой на 2 разряда множителя одновременно в прямых кодах сводится к сложению порядков, формированию знака произведения, преобразованию разрядов множителя согласно алгоритму и перемножению мантисс сомножителей.
Порядок произведения будет равен:
Рмн = 0.0010 10
Рмт = 0.001010
Рмн*мт = 0.0100 20
Результат закодирован в соответствии с заданием на кодировку множимого.
Знак произведения определяется суммой по модулю два знаков сомножителей:
ЗнМн 
зн Мт = 0 0 = 0.
Для умножения мантисс необходимо предварительно преобразовать множитель, чтобы исключить диаду 11 (34), заменив ее на триаду 10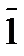 
и диаду 10 (24), заменив ее на триаду 1 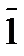0 . Преобразованный множитель имеет вид: Мтп4 =10120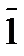
[Мт]п=0,10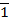 
2022 (преобразованный)
[Мн]д=0,0102232
[-Мн]д=3,3231101
[2Мн]д=0,0211130
| Структурная схема сумматора-умножителя 2-го типа. Алгоритм умножения «В», на 2 разряда множителя одновременно. |
| ЗН |
| S1 |
| P |
| S2 |
| h |
| F1 |
| F2 |
| h |
| h |
| h |
| Qn-1 |
| . . . |
| . . . |
| . . . |
| Qn |
| Qn-2 |
| Q1 |
| ОЧС |
| ОЧУС |
| ОЧС |
| ЗН |
| Ф Д К |
| ЗН |
| D1 |
| Dm |
| РЕГИСТР МНОЖИМОГО |
| Р Е Г И С Т Р М Н О Ж И Т Е Л Я |
| РЕГИСТР РЕЗУЛЬТАТА |
| . . . . |
| . . . |
| . . . |
| Dm+2 |
| Преобра-зовательмножи-теля |
| mul/sum 0 1 |
| Dm+1 |
| 0 1 0 1 |
| ОЧС |
| ОЧУС |
| ОЧС |
| ОЧУС |
| ОЧС |
| ОЧУС |
| ОЧС |
Умножение по алгоритмуВ:
| Четвертичная с/с | Двоично-четвертичная с/с | Комментарии | ||||
| Σ0 | ||||||
| П1 = [Мн]д | ||||||
| Σ1 | ||||||
| Σ1 * 4 | ||||||
| П2 = 0 | ||||||
| Σ2 | ||||||
| Σ2 * 4 | ||||||
| П3 = [-Мн]д | ||||||
| Σ3 | ||||||
| Σ3 * 4 | ||||||
| П4 = [2Мн]д | ||||||
| Σ4 | ||||||
| Σ4 * 4 | ||||||
| П5 = 0 | ||||||
| Σ5 | ||||||
| Σ5* 4 | ||||||
| П6 = [2Мн]д | ||||||
| Σ6 | ||||||
| Σ6 * 4 | ||||||
| П7= [2Мн]д | ||||||
| Σ7 |
После окончания умножения необходимо оценить погрешность вычислений. Для этого полученное произведение ((Мн*Мт)4=0,00102023123030 (РМн*PМт)4 = 20) приводится к нулевому порядку, а затем переводится в десятичную систему счисления:
(Мн*Мт)4 = 102023,123030;
(Мн*Мт)10 = 1163,4248.
Результат прямого перемножения операндов дает следующее значение:
Мн10*Мт10 = 18,72 * 62,17 = 1163,8224.
Абсолютная погрешность:
D = |1163,8224- 1163,4248| =0,3976.
Относительная погрешность:
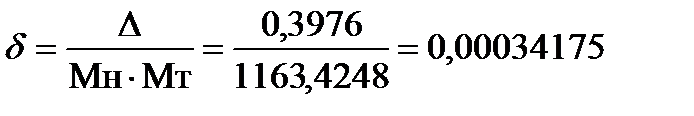(δ = 0,03417%)
Эта погрешность является суммарной, накопленной за счет приближенного перевода из 10 с/с в четверичную обоих сомножителей, а также за счет округления полученного результата произведения
Логический синтез одноразрядного четверичного сумматора
ОЧС - это комбинационное устройство, имеющее 5 входов и 3 выхода:
· 2 разряда одного слагаемого (множимого);
· 2 разряда второго слагаемого (регистр результата);
· вход переноса из младшего ОЧС.
Разряды обоих слагаемых закодированы : 0 - 10; 1 - 00; 2 - 01; 3 -11.
Логический базис для реализации – А2.
Принцип работы ОЧС описывается с помощью следующей таблицы истинности:
| A1 | A2 | B1 | B2 | p | П | S1 | S2 | Четверичная |
| 1+1+0=02 | ||||||||
| 1+1+1=03 | ||||||||
| 1+2+0=03 | ||||||||
| 1+2+1=10 | ||||||||
| 1+0+0=01 | ||||||||
| 1+0+1=02 | ||||||||
| 1+3+0=10 | ||||||||
| 1+3+1=11 | ||||||||
| 2+1+0=03 | ||||||||
| 2+1+1=10 | ||||||||
| 2+2+0=10 | ||||||||
| 2+2+1=11 | ||||||||
| 2+0+0=10 | ||||||||
| 2+0+1=03 | ||||||||
| 2+3+0=11 | ||||||||
| 2+3+1=12 | ||||||||
| 0+1+0=01 | ||||||||
| 0+1+1=02 | ||||||||
| 0+2+0=02 | ||||||||
| 0+2+1=03 | ||||||||
| 0+0+0=00 | ||||||||
| 0+0+1=01 | ||||||||
| 0+3+0=03 | ||||||||
| 0+3+1=10 | ||||||||
| 3+1+0=10 | ||||||||
| 3+1+1=11 | ||||||||
| 3+2+0=11 | ||||||||
| 3+2+1=12 | ||||||||
| 3+0+0=03 | ||||||||
| 3+0+1=10 | ||||||||
| 3+3+0=12 | ||||||||
| 3+3+1=13 |
Упрощение ОЧС картами Вейча
Для П
| a1a2b1b2p | ||||||||
| 1 | 1 | |||||||
Для S1
| a1a2b1b2p | ||||||||
Для S2
| a2 |
| |||||||||||
| p |
| p |
| a1 |
Результат минимизации функций по картам Карно-Вейча
ОЧС функция P
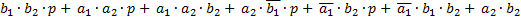
ОЧС функция S1
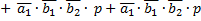
ОЧС функция S2
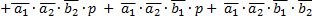
Реализация переключательной функции Q1 и P
Реализация переключательной функции Q2
Таблица истинности для ОЧС на мультиплексорах
| a1a2b1 | b2p | П | Псхема | S1 | S1схема | S2 | S2схема |
| b2p |  |  | |||||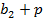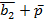
 |  |  | |||||
| | |  | |||||
| | |  | |||||
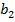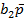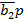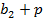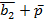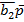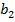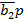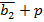| Const 0 |  | | |||||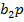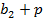
| |  | | |||||
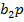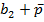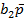| Const 1 | | | |||||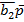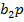
| | | | |||||
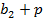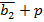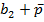Проверка L-экстремалей
Множество L-экстремалей E ={x001x0; x111x0; xxxx11; xx1x1x }
Z´ = Z - E ={100xxx; 111xxx; 1xx0xx; 1xxx1x; xxx11x; 1xxxx1 }
Проверка покрытия множества Z´ множеством найденных L-экстремалей Е
| L#E | ||||||||||
| x001x0 | Ø | Ø | ||||||||
| x111x0 | Ø | Ø | Ø | Ø | ||||||
| xxxx11 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | ||
| xx1x1x | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| Остаток | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
Конечное минимальное множество= { x001x0; x111x0; xxxx11; xx1x1x }
РАЗРАБОТКА АЛГОРИТМА УМНОЖЕНИЯ.
1. Перевод сомножителей из десятичной системы счисления в четвертичную:
Множимое:
18| 4 0,72 Мн4 =102,2324
16 4| 4 4
2 0| 1 2,88
4 в соответствии с заданной кодировкой множимого
3,52 Мн2/4 =010010,101110
4
2,08
4
0,32
Множитель:
62| 4 в соответствии с заданной кодировкой множимого
60|15| 4
2 12 3 Мт4 =332,022
3 Мт2/4 =111110,001010
0,17
4
0,68
4
2,72
4
2,88
2. Запишем сомножители в форме с плавающей запятой в прямом (дополнительном) коде (т.к. алгоритм В):
Мн =0,00010010101110 Рмн= 0.0100 +0310 - закодировано по заданию
Мт =0,00111110001010 Рмт = 0.0100 +0410 - закодировано традиционно
3. Умножение двух чисел с плавающей запятой на 2 разряда множителя одновременно в прямых кодах сводится к сложению порядков, формированию знака произведения, преобразованию разрядов множителя согласно алгоритму и перемножению мантисс сомножителей.
Порядок произведения будет равен:
Рмн = 0.0010 10
Рмт = 0.001010
Рмн*мт = 0.0100 20
Результат закодирован в соответствии с заданием на кодировку множимого.
Знак произведения определяется суммой по модулю два знаков сомножителей:
ЗнМн зн Мт = 0 0 = 0.
Для умножения мантисс необходимо предварительно преобразовать множитель, чтобы исключить диаду 11 (34), заменив ее на триаду 10 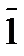и диаду 10 (24), заменив ее на триаду 1 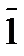0 . Преобразованный множитель имеет вид: Мтп4 =10120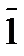
[Мт]п=0,10 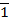2022 (преобразованный)
[Мн]д=0,0102232
[-Мн]д=3,3231101
[2Мн]д=0,0211130
| Структурная схема сумматора-умножителя 2-го типа. Алгоритм умножения «В», на 2 разряда множителя одновременно. |
| ЗН |
| S1 |
| P |
| S2 |
| h |
| F1 |
| F2 |
| h |
| h |
| h |
| Qn-1 |
| . . . |
| . . . |
| . . . |
| Qn |
| Qn-2 |
| Q1 |
| ОЧС |
| ОЧУС |
| ОЧС |
| ЗН |
| Ф Д К |
| ЗН |
| D1 |
| Dm |
| РЕГИСТР МНОЖИМОГО |
| Р Е Г И С Т Р М Н О Ж И Т Е Л Я |
| РЕГИСТР РЕЗУЛЬТАТА |
| . . . . |
| . . . |
| . . . |
| Dm+2 |
| Преобра-зовательмножи-теля |
| mul/sum 0 1 |
| Dm+1 |
| 0 1 0 1 |
| ОЧС |
| ОЧУС |
| ОЧС |
| ОЧУС |
| ОЧС |
| ОЧУС |
| ОЧС |
Умножение по алгоритмуВ:
| Четвертичная с/с | Двоично-четвертичная с/с | Комментарии | ||||
| Σ0 | ||||||
| П1 = [Мн]д | ||||||
| Σ1 | ||||||
| Σ1 * 4 | ||||||
| П2 = 0 | ||||||
| Σ2 | ||||||
| Σ2 * 4 | ||||||
| П3 = [-Мн]д | ||||||
| Σ3 | ||||||
| Σ3 * 4 | ||||||
| П4 = [2Мн]д | ||||||
| Σ4 | ||||||
| Σ4 * 4 | ||||||
| П5 = 0 | ||||||
| Σ5 | ||||||
| Σ5* 4 | ||||||
| П6 = [2Мн]д | ||||||
| Σ6 | ||||||
| Σ6 * 4 | ||||||
| П7= [2Мн]д | ||||||
| Σ7 |
После окончания умножения необходимо оценить погрешность вычислений. Для этого полученное произведение ((Мн*Мт)4=0,00102023123030 (РМн*PМт)4 = 20) приводится к нулевому порядку, а затем переводится в десятичную систему счисления:
(Мн*Мт)4 = 102023,123030;
(Мн*Мт)10 = 1163,4248.
Результат прямого перемножения операндов дает следующее значение:
Мн10*Мт10 = 18,72 * 62,17 = 1163,8224.
Абсолютная погрешность:
D = |1163,8224- 1163,4248| =0,3976.
Относительная погрешность:
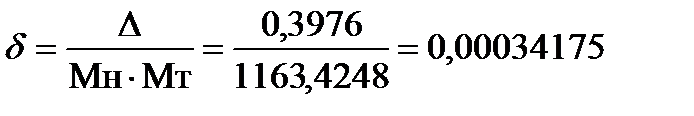(δ = 0,03417%)
Эта погрешность является суммарной, накопленной за счет приближенного перевода из 10 с/с в четверичную обоих сомножителей, а также за счет округления полученного результата произведения