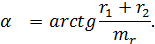Кусочно-линейная аппроксимация

Метод кусочно-линейной аппроксимации заключается в замене заданной нелинейной характеристики ломаной прямой с одной или несколькими точками излома. Такая замена нелинейной характеристики позволяет вести расчет аналитически с помощью линейных уравнений. Для прямолинейных участков записываются линейные уравнения, решения которых «припасовываются»: значения электрических величин для конца участка приравниваются соответствующим значениям для начала следующего участка.

Кусочно-линейная аппроксимация используется для расчета как установившихся, так и переходных процессов.

Наиболее просто решается задача в частном случае, когда нелинейность характеристики мала или когда участок характеристики, в пределах которого работает нелинейный элемент, известен и может быть аппроксимирован прямой без излома. В этом случае нелинейный элемент заменяется источником постоянной э. д. с. и линейным сопротивлением, равным дифференциальному сопротивлению этого элемента; цепь рассчитывается как линейная.

где

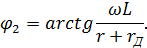
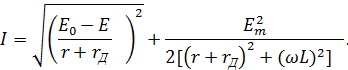
В общем случае при замене нелинейной характеристики ломаной линией схема замещения нелинейного сопротивления наряду с источниками и линейными резисторами включает в себя идеальные выпрямительные диоды (один или несколько). Идеальный диод имеет сопротивление, равное нулю при положительных значениях u и i и бесконечно большое при отрицательных u и i. Его вольтамперная характеристика имеет излом в точке u = 0, i = 0 (рисунок 5.3, б).

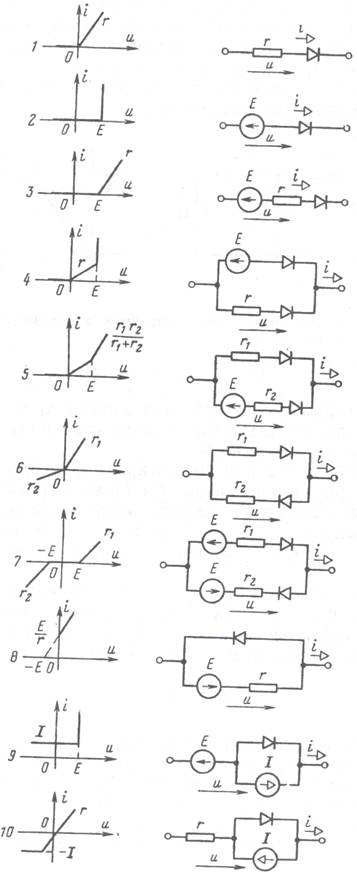
В таблице 5.1 показаны схемы замещения, соответствующие различным типам характеристик. Рекомендуется читателям самостоятельно графическим построением характеристик последовательно или параллельно соединенных элементов убедиться в том, что характеристики и схемы, приведенные в таблице 5.1, друг другу соответствуют. При этом следует обратить внимание на то, что перемена полярности идеального диода равносильна изменению положительных направлений тока и напряжения. Поэтому соответствие схем харак­теристикам обеспечивается как надлежащим подбором элементов, так и соответствующей полярностью включения идеальных диодов и источников.

Методом кусочно-линейной аппроксимации вольтамперных характеристик нелинейных резисторов, содержащихся в заданной электрической цепи, можно получить результирующую эквивалентную схему замещения всей цепи. В зависимости от постановки задачи может потребоваться построение вольтамперной характеристики (например, зависимости выходного напряжения от входного).

Графическое построение вольтамперных характеристик при последовательном, параллельном и смешанном соединениях, описанное ранее, применимо и для схемы с одним источником переменной э. д. с. или переменного тока.

Возможен и другой способ построения результирующей характеристики, основанный на том факте, что вольтамперная (или передаточная) характеристика цепи, имеющей кусочно-линейные элементы, должна быть кусочно-линейной Координаты точек излома результирующей характери­стики находятся из условия, что в изломе характеристики каждого идеального диода, входящего в эквивалентную схему замещения, напряжение и ток равны нулю.

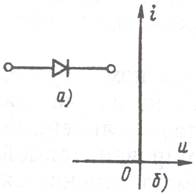
Рисунок 5.3 Диод (а) и характеристика идеального диода (б)

Таблица 5.1

Кусочно-линейные характеристики и схемы замещения

Построим в качестве примера вольтамперную характеристику I(u) для схемы рисунка 5.4, а.

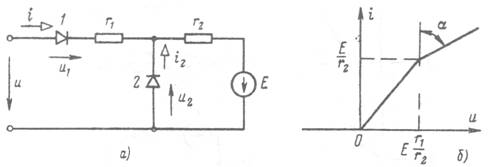
Рисунок 5.4 Построение кусочно-линейной вольтамперной характеристики цепи: а - схема; б - характеристика

В точке излома характеристики диода 1 u₁ = 0, i = 0. При этом ввиду отсутствия тока в сопротивлении r₁ ветвь с r₁ можно мысленно разомкнуть.

Идеальный диод 2 при этом открыт: i₂ = Е/r₂. В силу того, что напряжения на диодах 1 и 2 и на сопротивлении r₁ в этом случае равны нулю, входное напряжение получается также равным нулю: u = 0. Следовательно, первый излом вольтамперной характеристики находится в точке u = 0, i = 0.

Для диода 2 i₂ = 0 при u₂ = 0. При этом через сопротивление r₂ проходит ток Е/ r₂. Поскольку ток i₂ = 0, должно соблюдаться условие

i = Е/ r₂, причем вентиль 1 должен быть открыт, т е.u₁ = 0. Тогда:

u₁ = r₁ I = E r₁/ r₂

Следовательно, второй излом вольтамперной характеристики имеет координаты u = E r₁/ r_2, i = E / r₂

Между двумя найденными изломами характеристика прямолинейна (рисунок 5.1, б). Слева от первой точки излома диод 1 закрыт и i = 0; характеристика совпадает с отрицательной полуосью напряжений. Правее второй точки излома диод 1 открыт, а диод 2 закрыт; поэтому характери­стика продолжается под углом: