Игровые модели и их классификация

Определение 1. Конфликтной ситуацией (конфликтом)называют явление или ситуацию, в которой участвуют две или более стороны, имеющие различные интересы и обладающие возможностями применять для достижения своих целей разнообразные действия.

Определение 2. Упрощенную формализованную модель конфликтной ситуации называют игрой.

Замечание. От реального конфликта игра отличается наличием правил игры.

Теория игр – раздел прикладной математики, занимающийся построением математических моделей возможных конфликтных ситуаций и разработкой методов решения возникающих в этих ситуациях задач.

Определение 3. Заинтересованные стороны конфликта называют игроками.

Определение 4. Каждое действие игрока в рамках правил игры и в зависимости от ситуации, сложившейся в процессе игры, называют ходом или стратегией игрока.

Определение 5. Число, выражающее степень удовлетворения интересов игрока в данной ситуации, называют выигрышем игрока.

Определение 6. Зависимость величины выигрыша игрока от всевозможных стратегий называют функцией выигрыша (платежной функцией).

Определение 7. Значение функции выигрыша называют исходом игры.

Замечание. В теории игр предполагают, что функции выигрыша и множество доступных для каждого игрока стратегий известны, то есть каждый игрок знает как свои функции выигрыша и набор имеющихся в его распоряжении стратегий, так и функции выигрыша и стратегии остальных игроков. В соответствии с этой информацией он и организует свое поведение, то есть определяет выбор своей стратегии. Суть игры заключается в том, что каждый из игроков принимает такие решения, которые, как он полагает, могут обеспечить ему наилучший результат (исход).

Определение 8. Стратегию называют оптимальной, если она при многократном повторении обеспечивает данному игроку максимально возможный средний выигрыш.

Основные направления изучения теории игр

1) выработка принципов оптимальности – критериев, по которым поведение игроков следует считать оптимальным;

2) выяснение реализуемости принципов оптимальности – установление оптимальных в выработанном смысле ситуаций, отыскание их реализаций.

Определение 9. Игровую ситуацию называют равновесной (равновесием), если в ее нарушении не заинтересован ни один из игроков.

Замечание.Равновесие является одной из форм представления об оптимальности в игре, так как в равновесной ситуации каждый игрок получает наибольший выигрыш.

Определение 10.Если в игре существуют стратегии, приводящие к равновесной ситуации, то такие стратегии называют чистыми.

Определение 11. Если в игре не существует стратегий, приводящих к равновесной ситуации, но существуют комбинации исходных стратегий, приводящие к равновесию, то такие комбинации называют смешанными стратегиями.

Замечание.Часто смешанную стратегию представляют как случайный выбор игроками чистых стратегий, при котором случайные выборы различных игроков независимы в совокупности, а выигрыш каждого из них определяется как математическое ожидание случайного выигрыша.

Определение 12. Игру, в которой не существует равновесия, достигаемого чистыми стратегиями, но достигаемого смешанными стратегиями, называют смешанным расширением исходной игры.

Классификация игр

№ п/п	Признак	Класс игр
1.	Число игроков	Парные игры (два игрока)
Множественные игры (три и более игроков)
Игры с бесконечным числом игроков
2.	Количество стратегий	Конечные игры (конечное число стратегий у каждого игрока)
Бесконечные игры (бесконечное число стратегий у каждого игрока)
3.	Свойства функции выигрыша	Игры с нулевой суммой или антагонистические игры (выигрыш одного игрока равен проигрышу другого)
Игры с постоянной разностью (игроки выигрывают и проигрывают одновременно и им выгодно согласовывать свои действия)
Игры с ненулевой суммой (возможны и конфликты и согласованные действия)
4.	Возможность ведения переговоров	Кооперативные (коалиционные) игры (игроки могут договариваться о совместных стратегиях)
Некооперативные игры (игроки не имеют возможности договариваться)
5.	Характер действий игроков	Позиционные игры (игроки совершают действия последовательно, друг за другом)
Непозиционные игры (игроки действуют одновременно)

Матричные игры

Определение 13. Игру, в которой участвуют два игрока, называют парной игрой.

Пусть в игре участвуют два игрока А и В. Каждый из игроков располагает конечным числом чистых стратегий. Обозначим их соответственно: 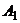, , 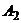…, 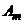– стратегии первого игрока, 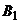, , 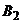…, 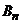– стратегии второго игрока. Игрок А может выбрать любую чистую стратегию 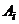, , 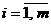в ответ на которую игрок В может выбрать любую свою чистую стратегию 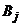, 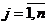. Если игра состоит только из личных ходов, то выбор пары стратегий 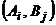однозначно определяет результат 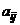– выигрыш игрока А. При этом проигрыш игрока В составит 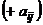(выигрыш игрока В равен 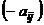). Если известны значения 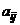для каждой пары 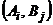чистых стратегий, то можно составить матрицу выигрышей игрока А (проигрышей игрока В) .

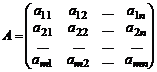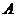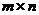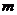Определение 14. Прямоугольную матрицу размерности , где (число строк) – число чистых стратегий первого игрока, а 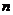(число столбцов) – число стратегий второго игрока, а в клетках указаны выигрыши игроков для каждой ситуации, называют платежной матрицей игры (матрицей выигрышей, матрицей платежей) первого игрока.

Определение 15. Игры двух игроков, функции выигрышей которых можно представить в виде матриц, называют матричными.

Замечание 1. Платежная матрица второго игрока: .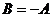

Замечание 2.Для наглядности матрицы выигрышей обоих игроков объединяют в биматрицу игры, элементами которой являются упорядоченные пары, состоящие из выигрыша первого и проигрыша второго игрока при данной стратегии:

.

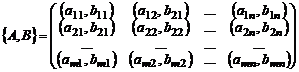Пример 40.1. Два игрока независимо друг от друга записывают любое целое число. Если выписанные числа имеют одинаковую четность, то игрок А получает от игрока В один рубль, а если разную, то наоборот, игрок А платит игроку В один рубль. Требуется составить платежную матрицу игры.

Решение. Игрок А имеет две стратегии: 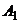– записать четное число, 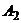– записать нечетное число. Игрок В также имеет две стратегии: 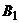– записать четное число, 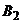– записать нечетное число. Выбор игроками соответствующих стратеги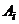й и 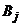однозначно определяет исход игры: 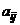– выигрыш игрока А. Стратегиям 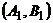и 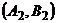соответствует выигрыш игрока А, равный одному рублю, а стратегиям 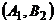и 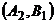соответствует проигрыш игрока, равный одному рублю. Тогда платежные матрицы игроков и биматрица игры будут иметь вид

, , .

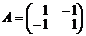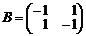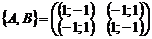Пример 40.2.Две фирмы функционируют на рынке одновременно с одинаковым товарным объемом 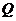. У обеих фирм по соображениям рентабельности есть следующие стратегии: либо вбросить на рынок полный объем товара 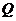, либо выбросить на рынок половину объема 0,5 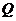. Если первая фирма выбрасывает на рынок полный объем товара, а вторая – половину объема, то первая фирма получает 100 % запланированной прибыли, а вторая – только 25 %, и наоборот. Если обе фирмы выбрасывают на рынок по полному объему прибыли, то получат по 15 % прибыли; если по половине объема, то прибыль каждой из фирм составит по 50 % от запланированной.

Решение. Обозначим 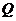– объем товара для каждой из фирм. Для первой фирмы возможны две стратегии: 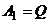, 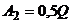(выбросить на рынок весь объем товара или его половину). Аналогично для второй фирмы: 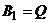, 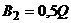(выбросить на рынок весь объем товара или его половину). Примем долю прибыли (в процентах от запланированной) за значение выигрыша при каждой стратегии. Тогда возможны следующие ситуаци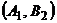и: и 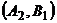– одна из фирм выбросила 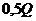товара, а другая 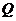товара; 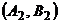– обе фирмы выбросили по 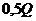товара. Запишем матрицы выигрышей обеих фирм и биматрицу игры:

, , .

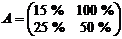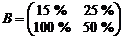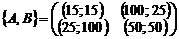Пример 40.3. Две конкурирующие фирмы борются за рынки сбыта, других конкурентов в этом сегменте нет (дуополия). В этом случае каждый из игроков может назвать цену p, по которой он хочет продать определенное количество товара. При этом полагается, что потребители приобретут товар у фирмы, объявившей меньшую цену. В случае объявления одинаковой цены спрос 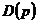распределяется между фирмами поровну.

Решение. Каждый из игроков обладает бесконечным числом стратегий. Функция выигрышей игроков характеризует величины дохода фирм в зависимости от объявленных цен. Так как доход фирмы 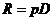, то функцию выигрышей игроков можно представить в виде