Глава 3. Аналитическая геометрия на плоскости

Глава 3. Аналитическая геометрия на плоскости

Прямая на плоскости

I. Уравнение прямой с угловым коэффициентом.

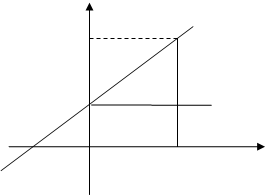Пусть на плоскости Оxy задана произвольная прямая, не параллельная оси Оу и образующая угол a с положительным направлением осиОх (0£a<p).

Возьмем на прямой произвольную точку М(х;у) (рис. 7). Проведем через точку N(0;в) прямую, параллельную осиОх, а из точки М опустим перпендикуляр на ось Ох.

Рис. 7

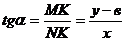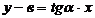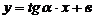Из треугольника NMK имеем . Отсюда или . Обозначив, 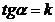, получим уравнение

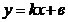(1).

Число 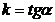называется угловым коэффициентом прямой, а уравнение (1) – уравнением прямой с угловым коэффициентом.

Если прямая проходит через начало координат, то в = 0 и, следовательно, уравнение этой прямой будет иметь вид

.

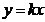Если прямая параллельна осиОх, то a = 0, следовательно 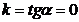и уравнение (1) примет вид

.

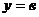Если прямая параллельна оси Оу, то 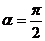и уравнение (1) теряет смысл, т.к. 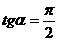не существует. В этом случае уравнение прямой будет иметь вид

х = а,

где а – абсцисса точки пересечения прямой с осьюОх.

II. Общее уравнение прямой.

Всякое уравнение первой степени относительно х и у, т.е. уравнение вида

Ах + Ву + С = 0(2)

(где А,В иС – постоянные коэффициенты, причем А² + В²¹ 0) определяет на плоскости некоторую прямую. Это уравнение называется общим уравнением прямой.

ЕслиВ = 0, то уравнение (2) имеет вид Ах + С = 0, т.е. 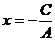- уравнение прямой, параллельной оси Оу.

ЕслиВ¹ 0, то из (2) получим уравнение вида y = kx + в - уравнение прямой с угловым коэффициентом (здесь ).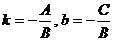

Если А = 0, то уравнение (2 ) приводится к виду 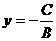- уравнение прямой, параллельной осиОх.

ЕслиС = 0, то из (2) получаем 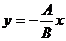- уравнение прямой, проходящей через начало координат.

III. Уравнение прямой, проходящей через две точки.

Если прямая проходит через точкиМ₁(х₁,у₁) и М₂(х₂,у₂), то ее уравнение имеет вид

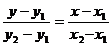. (3).

Предполагается, что в уравнении (3) .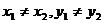

Если х₁ = х₂, то уравнение прямой имеет вид х = х₁, т.е. прямая параллельна оси Оу.

Если у₁ = у₂, то уравнение прямой имеет вид у = у₁, т.е. прямая параллельна осиОх.

IV. Уравнение прямой в отрезках.

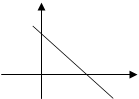Пусть прямая пересекает осьОх в точке М₁(а;0), а ось Оу – в точке М₂(0;в) (рис. 8).

Тогда уравнение (3) примет вид

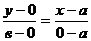или

Рис 8. 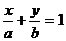(4).

Уравнение (4) называют уравнением прямой в отрезках.

V. Угол между двумя прямыми. Условия параллельности и перпендикулярности.

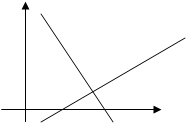
Пусть две прямые заданы уравнениями с угловыми коэффициентами y = k₁x + в и y = k₂x + в (рис. 9).

Рис. 9.

Найдем угол j между этими прямыми. Имеем 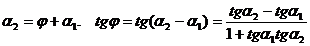. А т.к. 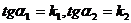, то

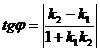(5).

Если прямые параллельны, то 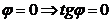. Из (5) получаем .

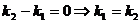Обратно, если 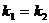, то 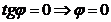и прямые параллельны. Следовательно, условием параллельности двух прямых является равенство их угловых коэффициентов: .

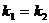Если прямые перпендикулярны, т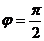о , но 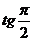не существует, а 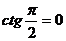. Из (5) получаем 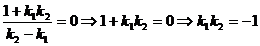. Справедливо и обратное. Следовательно, условием перпендикулярности двух прямых является равенство: k₁k₂ = -1.

Глава 3. Аналитическая геометрия в пространстве

Плоскость в пространстве

Рис. 18.

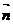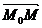При любом расположении точки М на плоскости Q векторы и перпендикулярны, поэтому их скалярное произведение равно нулю, т.е. 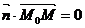или

А(х-х₀) + В(у-у₀) + С(z-z₀) = 0.(1)

Уравнение (1) есть уравнение плоскости, проходящей через данную точкуМ₀(х₀,у₀,z₀) перпендикулярно вектору 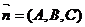. Вектор 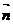называется нормальным вектором плоскости.

Прямая в пространстве

III. Общее уравнение прямой

Прямую в пространстве можно задать как линию пересечения двух непараллельныхз плоскостей. Система уравнений

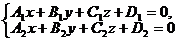(4)

есть общее уравнение прямой.

IY. Угол между двумя прямыми. Условия параллельности и перпендикулярности

Под углом между прямыми можно понимать угол между их направляющими векторами.

Пусть прямые задаются каноническими уравнениям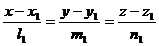и и 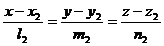. Тогда угол между ними определится по формуле

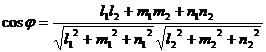(5).

Условие параллельности двух прямых:

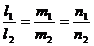; (6)

Условие перпендикулярности двух прямых:

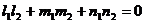. (7).

Глава 3. Аналитическая геометрия на плоскости

Прямая на плоскости

I. Уравнение прямой с угловым коэффициентом.

Пусть на плоскости Оxy задана произвольная прямая, не параллельная оси Оу и образующая угол a с положительным направлением осиОх (0£a<p).

Возьмем на прямой произвольную точку М(х;у) (рис. 7). Проведем через точку N(0;в) прямую, параллельную осиОх, а из точки М опустим перпендикуляр на ось Ох.

Рис. 7

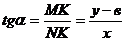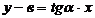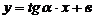Из треугольника NMK имеем . Отсюда или . Обозначив, 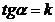, получим уравнение

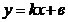(1).

Число 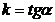называется угловым коэффициентом прямой, а уравнение (1) – уравнением прямой с угловым коэффициентом.

Если прямая проходит через начало координат, то в = 0 и, следовательно, уравнение этой прямой будет иметь вид

.

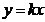Если прямая параллельна осиОх, то a = 0, следовательно 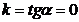и уравнение (1) примет вид

.

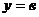Если прямая параллельна оси Оу, то 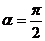и уравнение (1) теряет смысл, т.к. 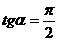не существует. В этом случае уравнение прямой будет иметь вид

х = а,

где а – абсцисса точки пересечения прямой с осьюОх.

II. Общее уравнение прямой.

Всякое уравнение первой степени относительно х и у, т.е. уравнение вида

Ах + Ву + С = 0(2)

(где А,В иС – постоянные коэффициенты, причем А² + В²¹ 0) определяет на плоскости некоторую прямую. Это уравнение называется общим уравнением прямой.

ЕслиВ = 0, то уравнение (2) имеет вид Ах + С = 0, т.е. 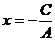- уравнение прямой, параллельной оси Оу.

ЕслиВ¹ 0, то из (2) получим уравнение вида y = kx + в - уравнение прямой с угловым коэффициентом (здесь ).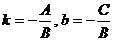

Если А = 0, то уравнение (2 ) приводится к виду 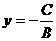- уравнение прямой, параллельной осиОх.

ЕслиС = 0, то из (2) получаем 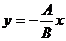- уравнение прямой, проходящей через начало координат.