Сумма двух случайных величин.

Пусть имеется система двух случайных величин X и Y, совместное распределение которых известно. Ставится задача найти распределение случайной величины 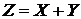. В качестве примеров СВ Z можно привести прибыль с двух предприятий; число определенным образом проголосовавших избирателей с двух разных участков; сумму очков на двух игральных костях.

1.Случай двух ДСВ. Какие бы значения ни принимали дискретные СВ (в виде конечной десятичной дроби, с разным шагом), ситуацию почти всегда можно свести к следующему частному случаю. Величины X и Y могут принимать только целые значения, т.е. где . Если изначально они являлись десятичными дробями, то целыми числами их можно сделать умножением на 10^k. А отсутствующим значениям между максимумами и минимумами можно приписать нулевые вероятности. Пусть известно совместное распределение вероятностей. Тогда, если пронумеровать строки и столбцы матрицы по правилам: 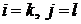, то вероятность суммы:

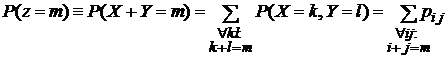
Элементы матрицы 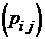складываются по одной из диагоналей.

2. Случай двух НСВ. Пусть известна совместная плотность распределения . Тогда плотность распределения суммы:

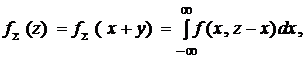
Если X и Y независимы, т.е. 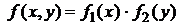, то

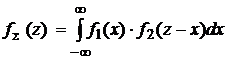
Пример 1. X , Y – независимые, равномерно распределенные СВ:

Найдём плотность распределения случайной величины .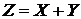

Очевидно, что ,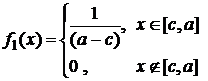

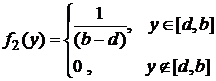СВ Z может принимать значения в интервале (c+d; a+b), но не при всех x. За пределами этого интервала . На координатной плоскости (x, z) областью возможных значений величины z является параллелограмм со сторонами x=с; x=a; z=x+d; z=x+b. В формуле для пределами интегрирования будут c и a. Однако ввиду того, что в производится замена y=z-x, при некоторых значениях z функция . Например, если c<d<a, то при z=x+c и любом x будем иметь: 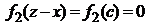. Поэтому вычисление интеграла следует осуществлять по отдельности для различных областей изменения величины z, в каждой из которых пределы интегрирования будут разными, но при всех x и z. Проделаем это для частного случая, когда а+d < b+c. Рассмотрим три различные области изменения величины z и для каждой из них найдём .

1) c+d ≤ z ≤ a+d. Тогда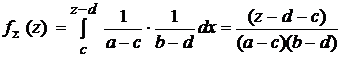

2) а+d ≤ z ≤ b+c. Тогда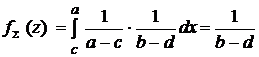

3) b+c ≤ z ≤ a+b. Тогда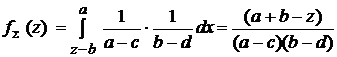

Такое распределение называется законом Симпсона. На рис.8, 9 изображены графики плотности распределения СВ 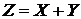при с=0, d=0.

рис.8 рис.9

Найти можно иначе, определяя сначала функцию распределения F(z) с помощью формулы геометрической вероятности, знаменателем которой является площадь указанного выше параллелограмма на координатной плоскости (x, z).

Пример 2. Пусть X , Y – система двух нормально распределенных СВ. Выражение для плотности вероятности 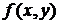приведено в п. 2.4.7. Производя в ней замену и интегрируя ее по x, получим: 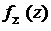имеет нормальное распределение с математическим ожиданием 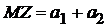и дисперсией . Это согласуется и с формулами, отражающими свойства математического ожидания и дисперсии (п. 2.1.5).