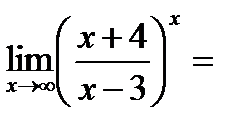Различные виды неопределенностей и их раскрытие
Ранее рассмотрели теоремы о пределах суммы, разности, произведения, частного, где пределы рассмотренных компонент существовали и были конечны. Рассмотрим случаи, когда пределы бесконечны или случай, когда предел делителя равен нулю.
I. Неопределенность вида 
Пусть 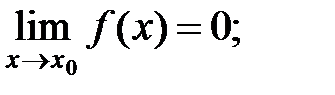
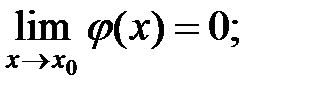

1) Пусть 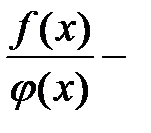 рациональная дробь (отношение двух многочленов).
рациональная дробь (отношение двух многочленов).
Выделить множитель  и сократить дробь на него. Такое сокращение возможно, т.к.
и сократить дробь на него. Такое сокращение возможно, т.к. 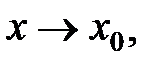 но
но  , т.е.
, т.е. 
Пример 9.1. 
2) Пусть 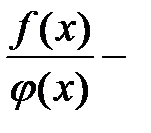 дробь, содержащая иррациональные выражения.
дробь, содержащая иррациональные выражения.
«Избавиться» от иррациональности, домножив числитель и знаменатель на соответствующее сопряженное выражение.
Пример 9.2. 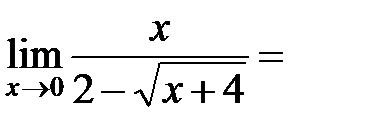
3) Для раскрытия неопределенности  , содержащей тригонометрические выражения, применяют 1-й замечательный предел.
, содержащей тригонометрические выражения, применяют 1-й замечательный предел.
II. Неопределенность вида 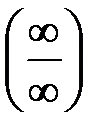
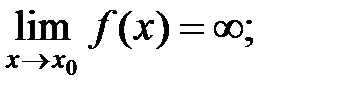
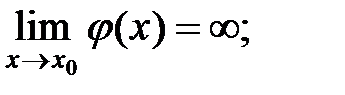

Для того, чтобы раскрыть неопределенность вида 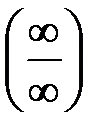 , заданную отношением двух многочленов, надо числитель и знаменатель разделить на наибольшую степень переменного.
, заданную отношением двух многочленов, надо числитель и знаменатель разделить на наибольшую степень переменного.
Пример 9.3. 
Пример 9.4. 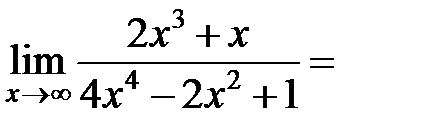
Пример 9.5. 
Замечание.  ,
, 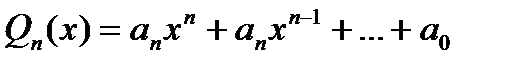 ,
, 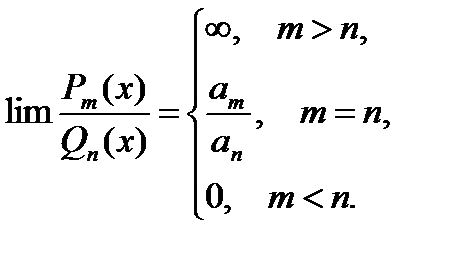
III. Неопределенность вида 
Неопределенность вида  преобразуется к неопределенности вида
преобразуется к неопределенности вида  или
или 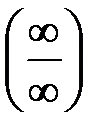 путем умножения и деления на сопряженную величину или приведения к общему знаменателю.
путем умножения и деления на сопряженную величину или приведения к общему знаменателю.
Пример 9.6. 
Пример 9.7. 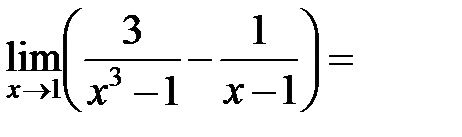
IV. Неопределенность вида 
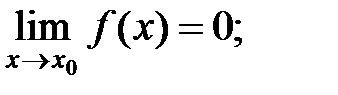
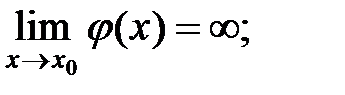
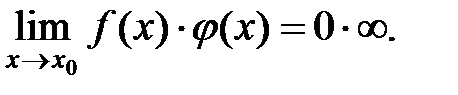
Неопределенность вида  сводится к неопределенности
сводится к неопределенности  или
или 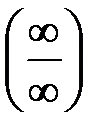 .
.
Пример 9.8. 
Первый признак существования предела
def.Переменная 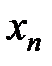 (числовая последовательность
(числовая последовательность 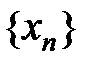 ) называется
) называется
· неубывающей, если 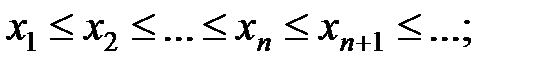
· возрастающей, если 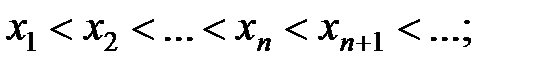
· невозрастающей, если 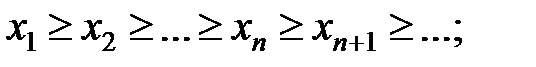
· убывающей, если 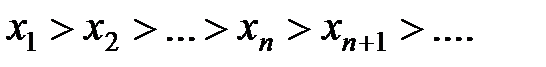
Возрастающие и убывающие переменные называются монотонными.
def. Переменная 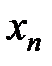 называется ограниченной сверху, если все ее значения не превосходят некоторого числа M, т.е.
называется ограниченной сверху, если все ее значения не превосходят некоторого числа M, т.е. 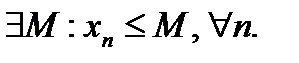
def. Переменная называется ограниченной снизу, если 
Теорема. Первый признак существования предела
Если переменная возрастает и ограничена сверху, то она имеет конечный предел.
Если переменная убывает и ограничена снизу, то она имеет конечный предел.
Второй признак существования предела переменной
Теорема (о сжатой переменной). Если для переменных  выполняется неравенство
выполняется неравенство  , и при этом
, и при этом 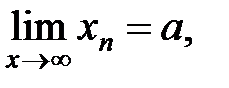
 , то
, то  .
.
Доказательство:
Первый замечательный предел
Функция 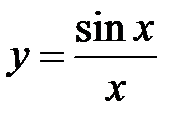 не определена при
не определена при 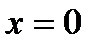 .
.
Рассмотрим 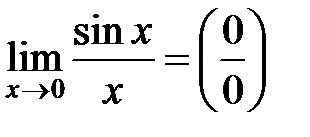 и докажем, что
и докажем, что 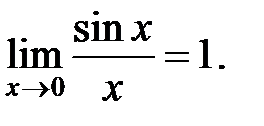
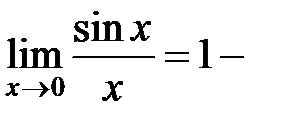 первый замечательный предел.
первый замечательный предел.
Доказательство:
Пример 12.1. 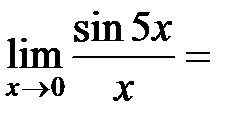
Пример 12.2. 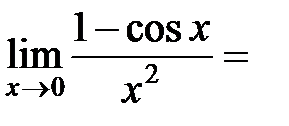
Второй замечательный предел
Рассмотрим переменную 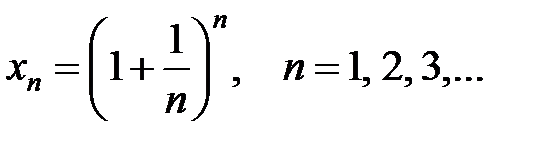
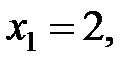
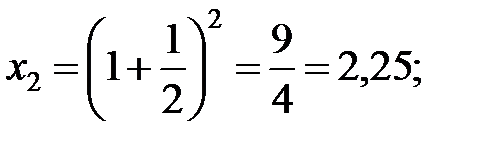
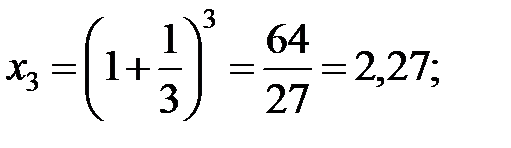
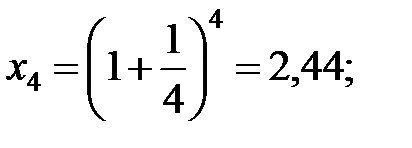
…………………….
Значения 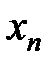 возрастают. Можно доказать, что
возрастают. Можно доказать, что 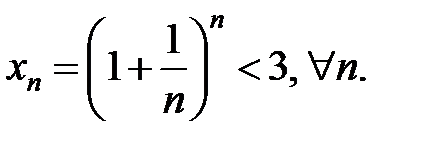
Переменная 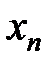 возрастает и ограничена сверху. По 1-му признаку существования переменной существует предел
возрастает и ограничена сверху. По 1-му признаку существования переменной существует предел 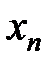 , а именно
, а именно
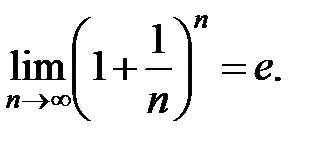
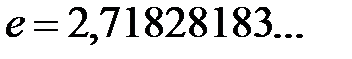
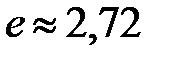 .
.
Логарифмы по основанию е называются натуральными и обозначаются 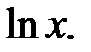
Докажем, что 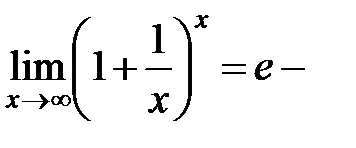 второй замечательный предел.
второй замечательный предел.
Неопределенность вида 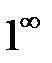 .
.
Доказательство.
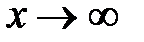 и принимает целые и дробные, положит-ые и отрицат-ые значения.
и принимает целые и дробные, положит-ые и отрицат-ые значения.
Рассмотрим случай, когда 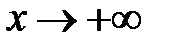 . Для любого положительного числа имеет место неравенство
. Для любого положительного числа имеет место неравенство 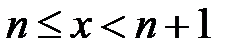 (*) (можно считать, что
(*) (можно считать, что 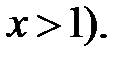
Перейдем к обратным величинам
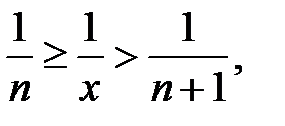 прибавим по 1,
прибавим по 1,
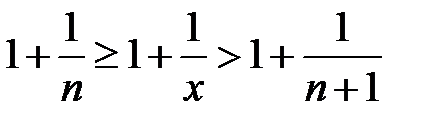 или
или 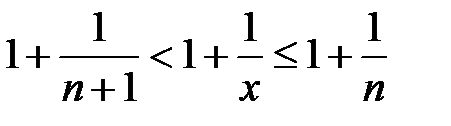 .
.
Возведем в степени с показателями из (*). Неравенство усилится
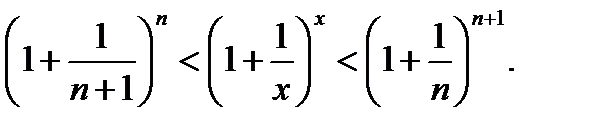
Найдем пределы крайних членов неравенства ( 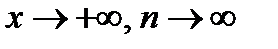 ).
).
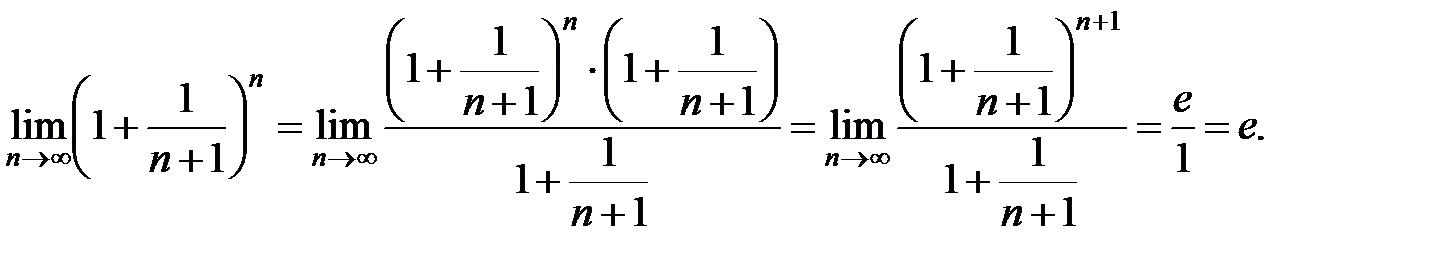
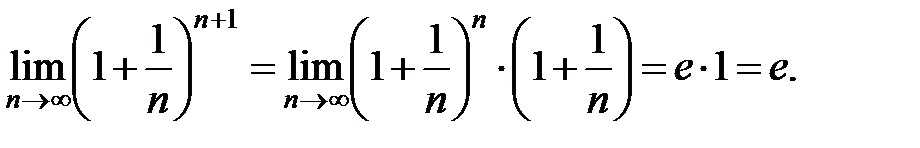
По теореме о сжатой переменной 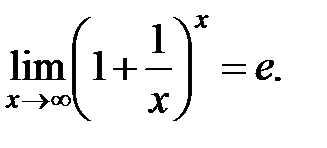
Можно доказать, что 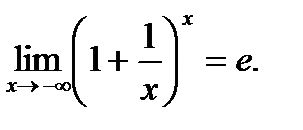
Таким образом, 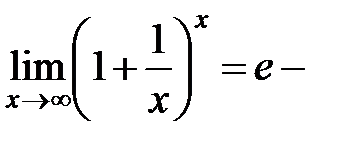 второй замечательный предел.
второй замечательный предел.
Положим 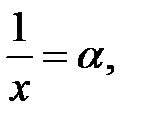 тогда
тогда 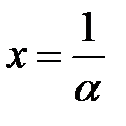 . Если
. Если 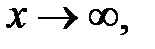 то
то 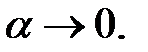
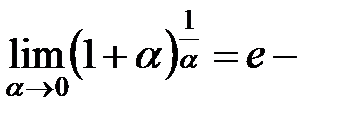 другая форма второго замечательного предела.
другая форма второго замечательного предела.
Пример 13.1. 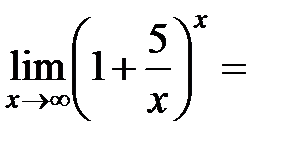
Пример 13.2. 
Пример 13.3.