Неопределенный и определенный интегралы функции

Методические указания,

Контрольные работЫ

По ДИСЦИПЛИНЕ «математикА»

Семестр

Для студентов специальностей

151001.65 «Технология машиностроения»,

200503.65 «Стандартизация и сертификация»,

190601.65 «Автомобили и автомобильное хозяйство».

Волгоград 2009

УДК 519.2

Рецензент:

канд. пед. наук Ребро И.В..

Методические указания, контрольные работы по дисциплине «Математика»

(2 семестр) для студентов специальностей 151001.65 «Технология машиностроения»,200503.65 «Стандартизация и сертификация»,190601.65 «Автомобили и автомобильное хозяйство». / С.Ю. Кузьмин; ВПИ (филиал) ВолгГТУ. – Волгоград, 2009. – 25с.

Методические указания предназначены для студентов заочной формы обучения высших технических учебных заведений, 190601.65 «Автомобили и автомобильное хозяйство»,151001.65 «Технология машиностроения», 200503.65 «Стандартизация и сертификация. Содержат решения типовых примеров, задания для контрольной работы.

Библиогр.: 6 названий

Ó Волгоградский государственный

технический университет, 2009

Ó Волжский политехнический

институт, 2009

Правила выполнения и оформления

Контрольных работ

При выполнении контрольных работ необходимо придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.

1. Каждая контрольная работа должна быть выполнена в отдельной тетради в клетку чернилами любого цвета, кроме красного.

2. В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер – последняя цифра в зачетке, название дисциплины, номер контрольной работы; здесь же следует указать название учебного заведения, дату отсылки работы в институт и адрес студента.

3. В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту. Контрольные работы, содержащие не все задачи задания, а также задачи не своего варианта, не зачитываются.

4. Решения задач надо располагать в порядке возрастания их номеров, указанных в заданиях, сохраняя номера задач.

5. Перед решением каждой задачи надо полностью выписать ее условие. В том случае, если несколько задач, из которых студент выбирает задачи своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными, взятыми из соответствующего номера.

6. Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.

7. После получения прорецензированной работы, как незачтенной, так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента.

Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок.

В случае незачета работы и отсутствия прямого указания рецензента о том, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.

При высылаемых исправлениях должна обязательно находиться прорецензированная работа и рецензия на нее. Поэтому рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается.

Контрольные задания

1. Вычислить неопределенные и определенные интегралы.

	а)	б)	в)
г)	д)
	а)	б)	в)
г)	д)
	а)	б)	в)
г)	д)
	а)	б)	в)
г)	д)
	а)	б)	в)
г)	д)
	а)	б)	в)
г)	д)
	а)	б)	в)
г)	д)
	а)	б)	в)
г)	д)
	а)	б)	в)
г)	д)
	а)	б)	в)
г)	д)

2. Найти общий интеграл дифференциального уравнения первого порядка с разделяющимися переменными

№	уравнение	№	уравнение

3.Найти общее решение однородного дифференциального уравнения 1-го порядка

№	уравнение	№	уравнение

4.Найти решение задачи Коши линейного дифференциального уравнения 1-го порядка

№	уравнение	№	уравнение
	,		, .
	, .
	, .		, .
	, .		,
	, .		,

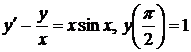5.Найти общее решение дифференциального уравнения в полных дифференциалах

№	уравнение	№	уравнение

6.Найти решение дифференциального уравнения допускающее понижение порядка

№	уравнение	№	уравнение

7.Найти решение задачи Коши дифференциального уравнения допускающее понижение порядка

№	уравнение	№	уравнение
			, ,
	, ,
	, ,		, ,
	, ,		, ,
	, , .		, , .

8.Найти общий интеграл дифференциального уравнения первого порядка с разделяющимися переменными

№	уравнение	№	уравнение
	а) ; b) ; c) .		а) ; b) ; c) .
	а) ; b) ; c) .		а) ; b) ; c) .
	а) ; b) ; c) .		а) ; b) ; c) .
	а) ; b) ; c) .		а) ; b) ; c) .
	а) ; b) ; c) .		а) ; b) ; c) .

Методические указания по решению варианта 00

1.Вычислить неопределенные и определенные интегралы

а) = =

б) .

Интегирируется по частям: пусть ; тогда , . Следовательно, .

Получившийся интеграл вычисляется методом замены переменной:

. Тогда

;

в)

.

г) = = =

= + =0.

д)

2.Решите дифференциальное уравнение первого порядка с разделяющимися переменными .

Разделяем переменные: . Интегрируем: .

Получаем: или .

3.Решите однородное дифференциальное уравнение первого порядка .

Делаем замену: .

Подставляем в исходное уравнение:

Разделяем переменные: .

Интегрируя: , получаем:

Переходя от вспомогательной функции обратно к функции у, получаем общее решение:

4. Найти решение задачи Коши

Решим методом Бернулли.

Полагаем , .

Тогда , .

1) , , , .

2) , т.е. , .

- общее решение.

Подставим начальные значения . Решаем уравнение и получаем что с=e,

Итак, .

5. Найти общий интеграл дифференциального уравнения

.

Проверим выполнение теоремы: Þ левая часть дифференциального уравнения есть полный дифференциал некоторой функции . Найдем ее:

. Так как. C, получим .

6.Найти общее решение дифференциального уравнения .

Применяем подстановку: .

Получаем: .

Произведя обратную замену, получаем:

. Общее решение исходного дифференциального уравнения: .

7.Найти решение задачи Коши с начальными условиями

x₀ = 0; y₀ = 1;

Решаем с помощью понижения порядка:

Подставим начальные условия:

.

Получаем частное решение (решение задачи Коши):

8.Найти общее решение дифференциального уравнения

Замена переменной: .

Тогда .

1) .

Произведем замену переменной: . Отсюда, . Подставляем:

. С учетом того, что , получаем: .

Таким образом, общий интеграл имеет вид:

2) .

9.Найти общее решение дифференциального уравнения .

Решим соответствующее однородное уравнение:

Найдем частное решение исходного неоднородного уравнения.

Правая часть уравнения - корень кратности 1 характеристического уравнения. Частное решение ищем в виде:

Имеем: .

Определим неизвестные коэффициенты А и В. Подставим частное решение в общем виде в исходное неоднородное дифференциальное уравнение:

Следовательно, частное решение:

Общее решение линейного неоднородного дифференциального уравнения:

10.Найти общее решение дифференциального уравнения

Правую часть дифференциального уравнения представим в виде суммы двух функций f₁(x) + f₂(x) = x + (-sin(2x)).

Составим и решим характеристическое уравнение: .

1. Для функции f₁(x)=ax+b число 0 не является корнем характеристического уравнения тогда, . Имеем:

. Получаем: .

2. Для функции f₂(x) , где . Число не является корнем характеристического уравнения, тогда

.

Подставляем:

Получаем . Следовательно, искомое частное решение имеет вид: . Общее решение неоднородного дифференциального уравнения имеет вид:

Вопросы к экзамену по теоретическому курсу

МАТЕМАТИКА (II семестр)

Одной переменной

1. Первообразная и неопределенный интеграл, их свойства.

2. Основные методы интегрирования: при помощи разложения подынтегральной функции, замена переменной, интегрирование по частям.

3. Определенный интеграл, основные свойства, геометрический смысл.

4. Формула Ньютона – Лейбница о вычислении определенных интегралов. Замена переменной и интегрирование по частям в определенном интеграле.

5. Несобственные интегралы.

6. Вычисление площадей плоских фигур в прямоугольных, параметрических и полярных координатах с помощью определенного интеграла.

7. Вычисление длины дуги плоской кривой в прямоугольных, параметрических и полярных координатах с помощью определенного интеграла.

8. Вычисление объема тела образованного вращением вокруг оси с помощью определенного интеграла.

9. Механические приложения определенного интеграла.

Дифференциальные уравнения

10. Дифференциальные уравнения первого порядка: основные понятия.

11. Дифференциальные уравнения с разделяющимися переменными.

12. Однородные и приводящиеся к однородным дифференциальные уравнения.

13. Линейные уравнения. Метод Бернулли.

14. Уравнение в полных дифференциалах.

15. Дифференциальные уравнения высших порядков, основные понятия. Уравнения, допускающие понижение порядка.

16. Линейные дифференциальные уравнения высших порядков.

17. Линейные однородные дифференциальные уравнения второго и высших порядков.

18. Интегрирование линейных однородных дифференциальных уравнений второго порядка.

19. Линейные неоднородные дифференциальные уравнения второго и высших порядков. Метод вариации произвольных постоянных. Линейные неоднородные дифференциальные уравнения со специальной правой частью.

20. Системы дифференциальных уравнений.

СПИСОК ЛИТЕРАТУРЫ

1. Агишева Д.К, Короткова Н.Н, Мустафина Д.А.. Математика. II часть. Учеб. пособие / ВолгГТУ, ВПИ (филиал), Волгоград, 2004. – 94с.

2. Букин Т.Е., Малов Н.В. Введение в анализ: Методические указания курса высшей математики для студентов вечерних факультетов/ ВолгПИ. – Волгоград, 1986 г. – 25с.

3. Мустафина Д.А., Ребро И.В., Кузьмин С.Ю., Антипина С.Г. Интегральное исчисление функции одной переменной: Учеб. пособие / ВолгГТУ. – Волгоград, 2007. – 97 с.

4. Мустафина Д.А., Ребро И.В., Кузьмин С.Ю., Короткова Н.Н. Дифференциальное исчисление функции одной и нескольких переменных с приложениями : Учеб. пособие / ВолгГТУ. – Волгоград, 2009. – 128 с.

5. Ребро И.В., Кузьмин С.Ю., Короткова Н.Н., Мустафина Д.А.. Дифференциальные уравнения: Учеб. пособие / ВолГТУ. – Волгоград, 2006. 64с.

6. Шапкин А.С. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями: Учеб. пособие. – 3-е изд. –М.: Издательско-торговая корпорация «Дашков и К0», 2006. -432 с.

№			№

Приложение 1.

Таблица дифференцирования сложных функций

Приложение 2.

Таблица интегрирования основных элементарных функций

Методические указания,

Контрольные работЫ

По ДИСЦИПЛИНЕ «математикА»

Семестр

Для студентов специальностей

151001.65 «Технология машиностроения»,

200503.65 «Стандартизация и сертификация»,

190601.65 «Автомобили и автомобильное хозяйство».

Волгоград 2009

УДК 519.2

Рецензент:

канд. пед. наук Ребро И.В..

Методические указания, контрольные работы по дисциплине «Математика»

(2 семестр) для студентов специальностей 151001.65 «Технология машиностроения»,200503.65 «Стандартизация и сертификация»,190601.65 «Автомобили и автомобильное хозяйство». / С.Ю. Кузьмин; ВПИ (филиал) ВолгГТУ. – Волгоград, 2009. – 25с.

Методические указания предназначены для студентов заочной формы обучения высших технических учебных заведений, 190601.65 «Автомобили и автомобильное хозяйство»,151001.65 «Технология машиностроения», 200503.65 «Стандартизация и сертификация. Содержат решения типовых примеров, задания для контрольной работы.

Библиогр.: 6 названий

Ó Волгоградский государственный

технический университет, 2009

Ó Волжский политехнический

институт, 2009

Правила выполнения и оформления

Контрольных работ

При выполнении контрольных работ необходимо придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.

1. Каждая контрольная работа должна быть выполнена в отдельной тетради в клетку чернилами любого цвета, кроме красного.

2. В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер – последняя цифра в зачетке, название дисциплины, номер контрольной работы; здесь же следует указать название учебного заведения, дату отсылки работы в институт и адрес студента.

3. В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту. Контрольные работы, содержащие не все задачи задания, а также задачи не своего варианта, не зачитываются.

4. Решения задач надо располагать в порядке возрастания их номеров, указанных в заданиях, сохраняя номера задач.

5. Перед решением каждой задачи надо полностью выписать ее условие. В том случае, если несколько задач, из которых студент выбирает задачи своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными, взятыми из соответствующего номера.

6. Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.

7. После получения прорецензированной работы, как незачтенной, так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента.

Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок.

В случае незачета работы и отсутствия прямого указания рецензента о том, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.

При высылаемых исправлениях должна обязательно находиться прорецензированная работа и рецензия на нее. Поэтому рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается.

Контрольные задания

1. Вычислить неопределенные и определенные интегралы.

	а)	б)	в)
г)	д)
	а)	б)	в)
г)	д)
	а)	б)	в)
г)	д)
	а)	б)	в)
г)	д)
	а)	б)	в)
г)	д)
	а)	б)	в)