Учет ограничений на значения переменных

Существенный вклад в математическую теорию экстремальных задач был внесен Л.В. Канторовичем, впервые сформулировавшим и решившим задачу, позднее получившую название задачи линейного программирования. Математическая постановка этой задачи сводится к поиску переменных, входящих в выражение линейной критериальной функции и, в общем случае, в неограниченное конечное количество дополнительных функций ограничений (тоже линейных), которые в частности могут представлять собой неравенства. Дальнейшее развитие идей Л.В. Канторовича привело к появлению теории математического программирования, расширившей класс используемых функций. Так в некоторых случаях удается решать задачи с нелинейными критериальными функциями (задачи квадратичного программирования, геометрического программирования и т. п.). Отметим, что термин программирование в данном случае используется только как название математического метода и непосредственного отношения к программированию на ЭВМ не имеет.

Рассмотрим простейшую задачу математического программирования, у которой имеется линейная целевая функция и линейные ограничения. Такая задача называется задачей линейного программирования. Будем считать, что у этой задачи имеется 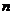переменных и 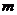ограничений. Тогда целевая функция 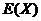может быть записана в виде:

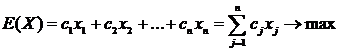(1)

Если по смыслу задачи целевая функция должна обращаться в минимум, то для получения выражения (1) в ней достаточно поменять значения всех коэффициентов 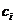на противоположные ( ).

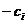Набор ограничений может быть записан в виде:

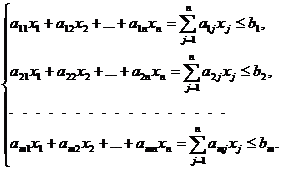(2)

Тогда исходными данными (параметрами задачи) являются наборы коэффициентов 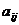, , 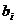, 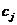а ее решением – значения 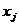, удовлетворяющие выражениям (1, 2). Кроме этого, в задачах, связанных с экономикой и менеджментом, обычно имеет место набор дополнительных 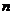ограничений 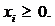Отметим, что параметры задачи связанны со значениями решения 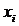выражениями вида

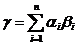(3)

Оптимальное решение рассматриваемой задачи линейного программирования 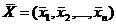представляет собой набор переменных, обеспечивающих максимум значения целевой функции 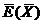. Отыскание этого набора представляет собой математическую задачу, которая может быть решена различными способами.

Задача линейного программирования при 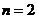допускает достаточно наглядную геометрическую интерпретацию. Например, если задача поиска экстремума имеет вид

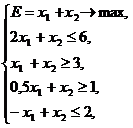
то может быть найдено ее плоскостное решение (рис. 4). Здесь ребра четырехугольника 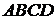образуют область допустимых значений переменных, заданную соответствующими ограничениями. Оптимальное решение может быть найдено за счет перемещения графика целевой функции 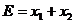параллельно самому себе до тех пор, пока он не пройдет через точку 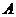. В этом случае оптимальное решение является единственным. Если бы целевая функция имела вид 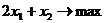, то имело бы место бесконечное множество оптимальных решений, лежащих на отрезке .

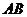Распространенным методом решения задачи линейного программирования является так называемый симплекс – метод. В его основе лежит так называемая симплекс-таблица, которая составляется по определенным правилам исходя из исходных данных задачи (1, 2). Доказано, что, производя последовательные преобразования этой таблицы по определенным правилам, можно получить оптимальное решение задачи линейного программирования [1].

В основе методов решения нелинейных задач с ограничениями лежит так называемый метод Лагранжа. Наличие ограничения сужает возможности отыскания экстремума. В этом случае, как правило, экстремум функции 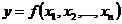не совпадает с локальным экстремумом, определенным с помощью классического метода и называется условным. Для решения подобных задач строится специальная функция, обычно называемая функцией Лагранжа

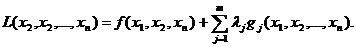
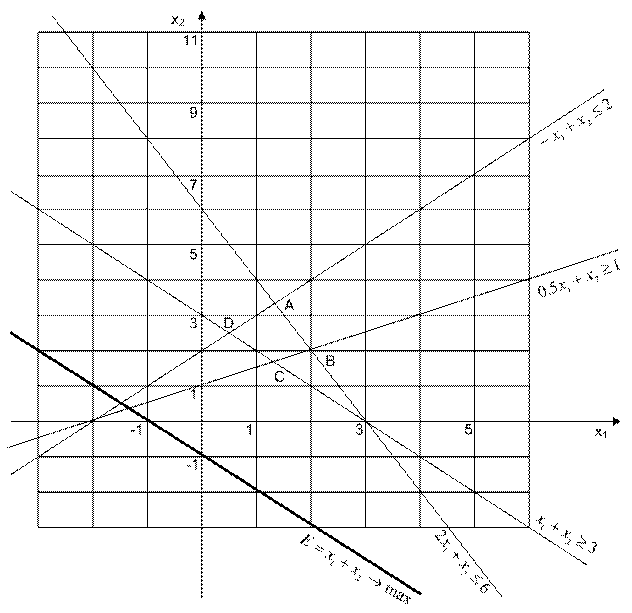
Рис. 4. Графическая интерпретация метода линейного программирования

В отличие от обычной функции 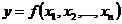функция Лагранжа имеет дополнительно 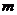переменных 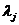по числу ограничений. Основная идея метода сводится к отысканию экстремумов функции Лагранжа ранее рассмотренным способом приравнивания к нулю частных производных. После отыскания локальных экстремумов функции Лагранжа необходимо выбрать среди них те, которые обеспечивают в зависимости от условия задачи наибольшее или наименьшее значение функции .

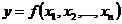Набор множителей Лагранжа 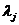имеет определенный смысл, заключающийся в том, что их значение определяет величину изменения оптимального решения в зависимости от изменения соответствующего ограничения. Уравнения ограничений могут быть записаны в виде неравенств, например:

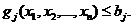
При решении таких задач приходится выполнять итеративную процедуру отыскания экстремума, задавая область допустимых значений переменных 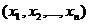. Экстремум целевой функции может достигаться в этом случае как внутри области, так и на ее границе. Для построения области допустимых решений следует записать уравнения линий уровня целевой функции – множество точек плоскости, в которых целевая функция постоянна.

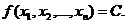
Определив направление возрастания (убывания) целевой функции, построив, например, линии уровня для разных значений 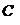, линия уровня перемещается в нужном направлении внутри области допустимых значений переменных с целью отыскания наибольшего (наименьшего) значения.