Рассмотрим матрицу специального вида
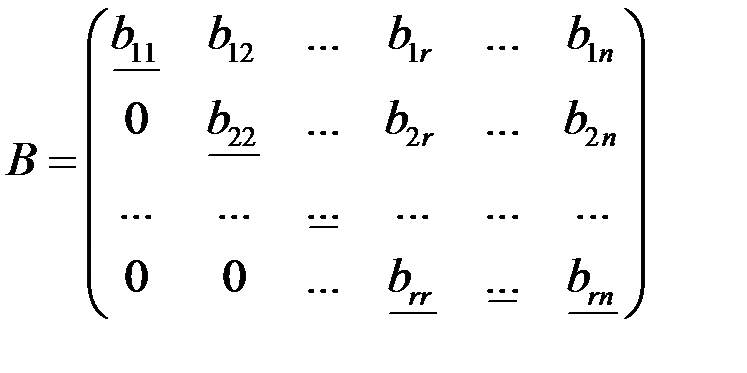
в которой все «диагональные элементы» 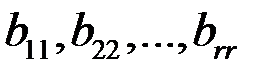 отличны от нуля, а все элементы расположенные ниже диагональных, равны нулю. Такую матрицу будем называть трапециевидной. При r = n она будет треугольной.
отличны от нуля, а все элементы расположенные ниже диагональных, равны нулю. Такую матрицу будем называть трапециевидной. При r = n она будет треугольной.
Теорема 2.Ранг трапециевидной матрицы равен числу ее ненулевых строк.
Теорема 3.Всякую матрицу можно с помощью конечного числа элементарных преобразований привести к трапециевидному виду.
Метод Гаусса вычисления ранга матрицы состоит в приведении матрицы к трапециевидному виду и в подсчете ее ненулевых строк.
Пример 3
Найти ранг матрицы 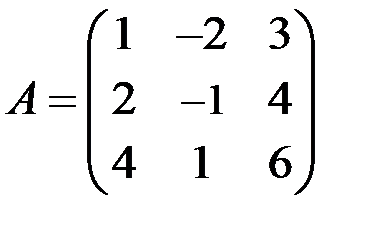 .
.
Решение
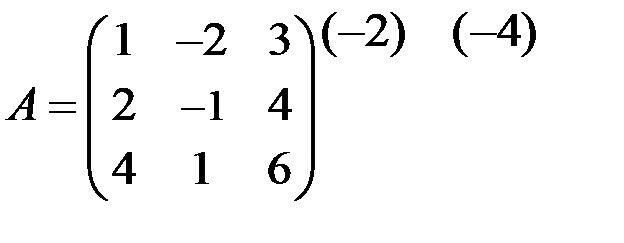 ~
~ 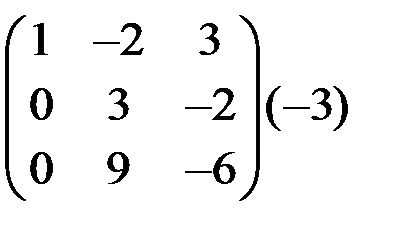 ~
~ 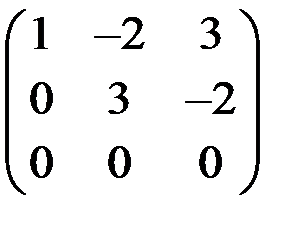
На первом шаге первую строку матрицы умножили на (-2) и сложили со второй строкой, умножили первую строку на (-4) и сложили с третьей строкой. На втором шаге вторую строку умножили на (-3) и сложили с третьей строкой. Нулевую строку вычеркнули. Таким образом, ранг матрицы r = 2.
Метод Гаусса решения СЛАУр
Пусть дана система линейных алгебраических уравнений (СЛАУр)
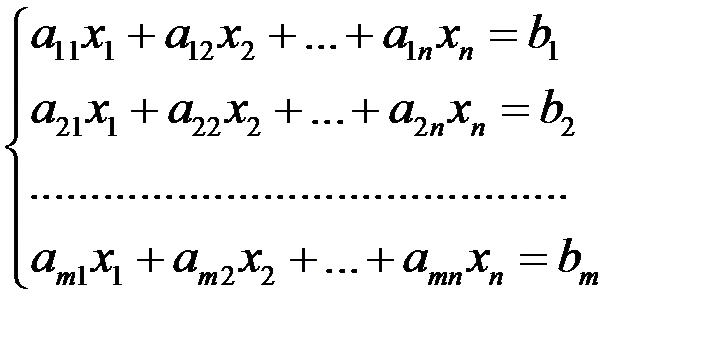
Поставим задачу: исследовать данную систему, т.е. выяснить, не решая ее, совместна она или несовместна, а если совместна, то определенна она или неопределенна.
На все эти вопросы отвечает теорема Кронекера - Капелли.
Пусть дана матрица системы 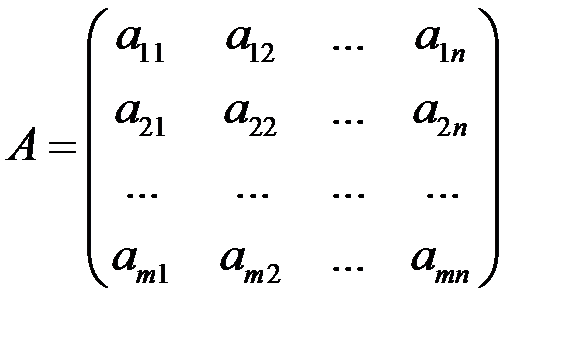 .
.
Рассмотрим расширеннуюматрицу системы
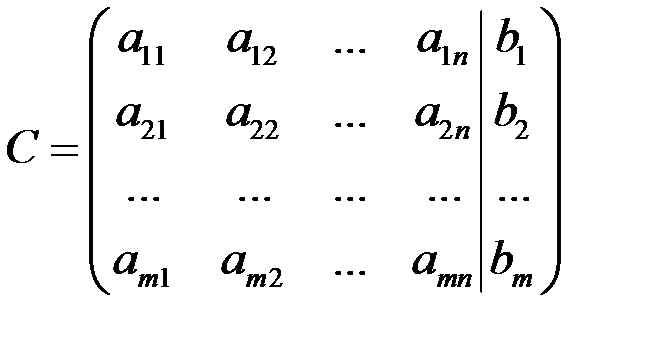 .
.
Теорема Кронекера – Капелли.
СЛАУр совместна тогда и только тогда, когда ранг расширенной матрицы равен рангу матрицы системы:
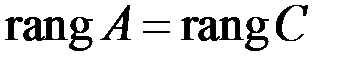 или
или 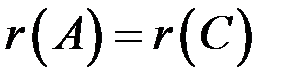 .
.
Замечание
Если 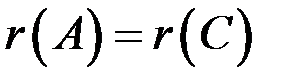 и
и 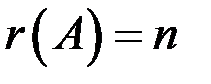 , где n – число неизвестных, то система определенна; если
, где n – число неизвестных, то система определенна; если 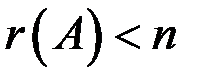 , то система неопределенна, если же
, то система неопределенна, если же 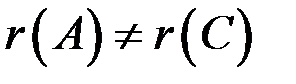 , то система несовместна.
, то система несовместна.
Метод Гаусса решения СЛАУр состоит в следующем.
1. Выписывают расширенную матрицу системы
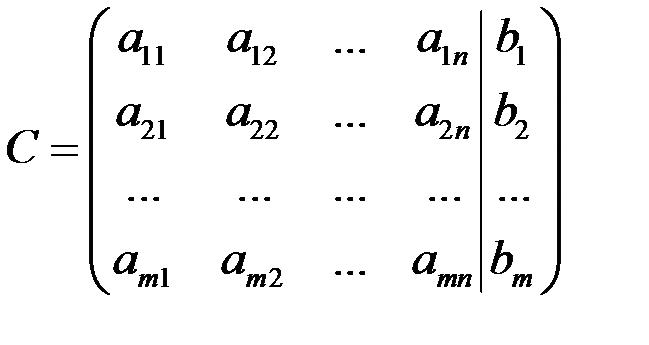
и с помощью элементарных преобразований приводят ее к трапециевидному виду.
2. Применяя теорему Кронекера – Капелли, исследуют систему, получая один из случаев:
– система совместна и определенна,
– система совместна и неопределенна,
– система несовместна.
Трапециевидная форма расширенной матрицы С в каждом из этих случаев имеет вид:
1) С~ 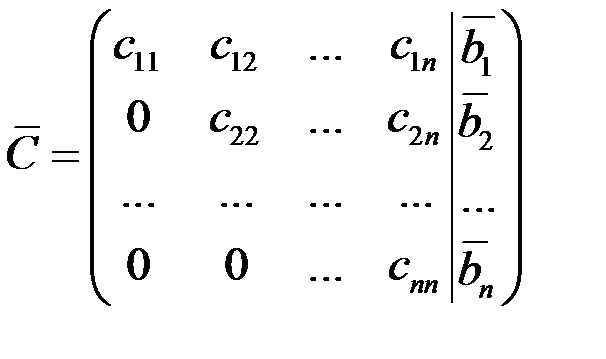
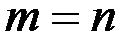 ,
, 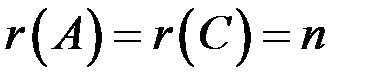 ,
,
следовательно, система определенна, имеет единственное решение,
2) С~ 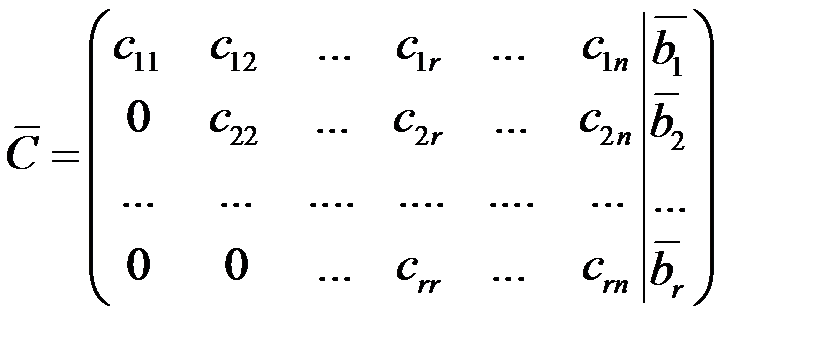
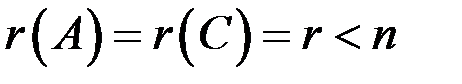 ,
,
следовательно, система неопределенна, имеет бесконечное множество решений,
3) если какая-либо строка матрицыС имеет вид 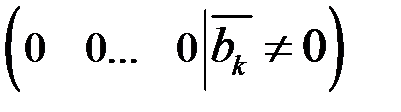 , то система несовместна (решений нет).
, то система несовместна (решений нет).
3. Для решения системы, если оно существует, следует записать новую систему, отвечающую полученной трапециевидной матрице, которая является более простой по сравнению с исходной и решить ее (обратный ход).
Пример 4
Исследовать и решить СЛАУр: 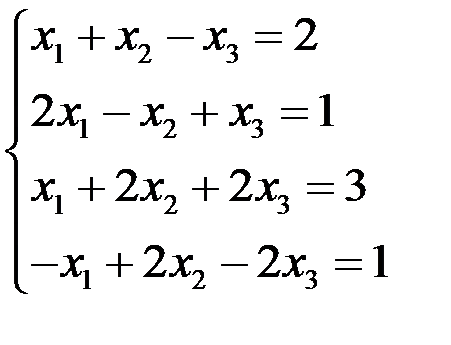 .
.
Решение
Составим расширенную матрицу и проведем над ней эквивалентные преобразования для определения 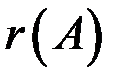 и
и 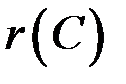 .
.
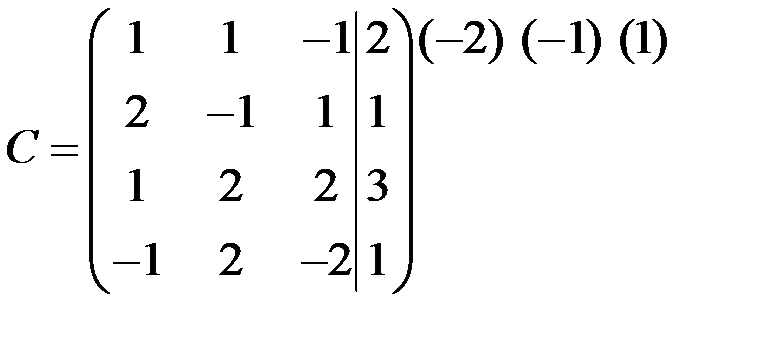 ~
~ 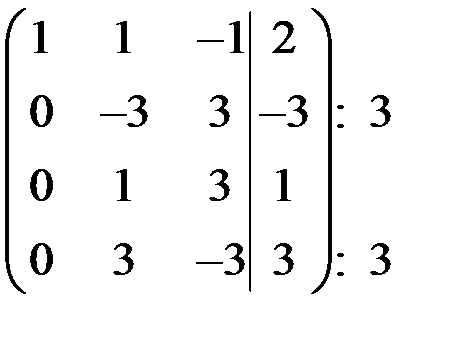 ~
~
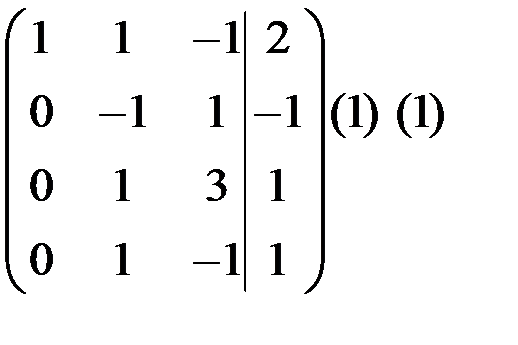 ~
~ 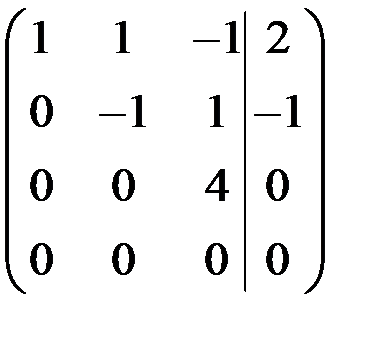 ,
,
Таким образом, 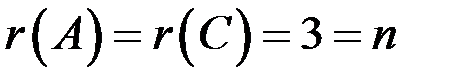 , следовательно, по теореме Кронекера – Капелли система совместна и определенна.
, следовательно, по теореме Кронекера – Капелли система совместна и определенна.
Составим систему, соответствующую последней матрице, эквивалентную исходной:
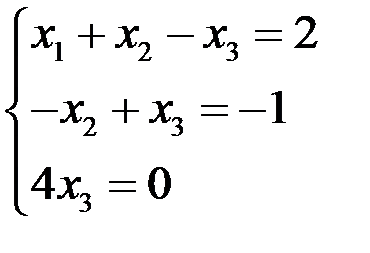 Þ
Þ 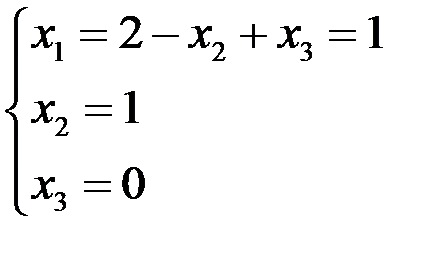 .
.
Таким образом, 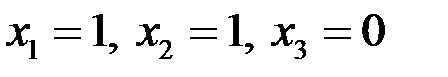 .
.
Пример 5
Исследовать и решить СЛАУр: 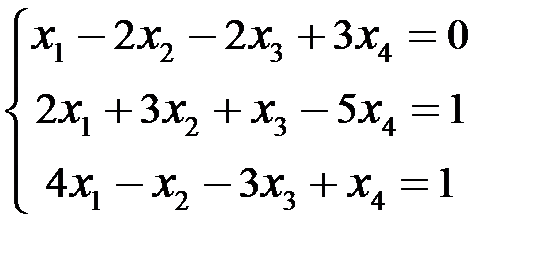 .
.
Решение
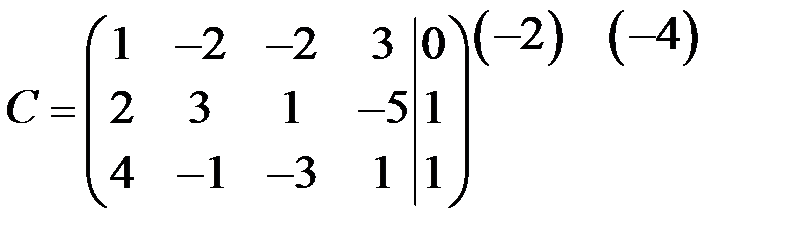 ~
~ 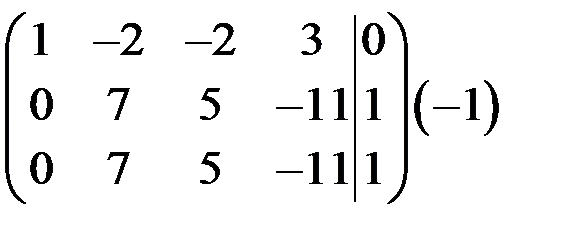 ~
~ 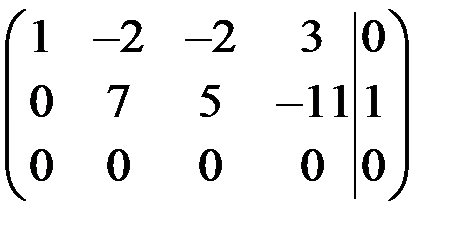
Так как 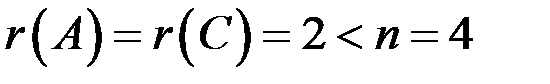 ,следовательно, система совместна и неопределенна (имеет бесчисленное множество решений).
,следовательно, система совместна и неопределенна (имеет бесчисленное множество решений).
Последней матрице соответствует система:
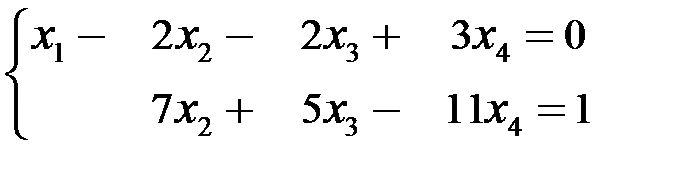 Þ
Þ 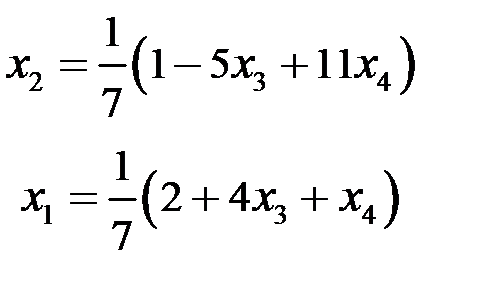
где 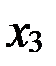 и
и 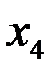 – произвольные параметры.
– произвольные параметры.
Пример 6
Исследовать и решить СЛАУр: 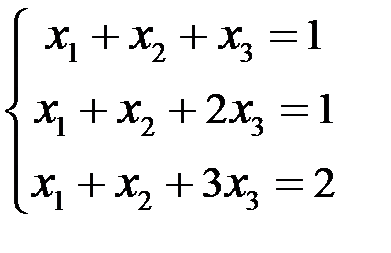
Решение
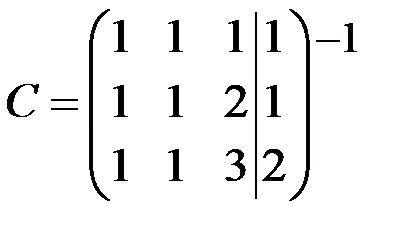 ~
~ 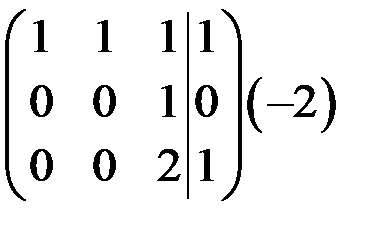 ~
~ 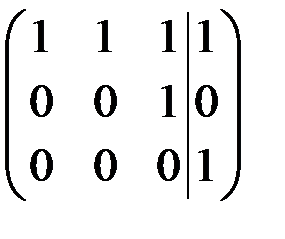
Так как 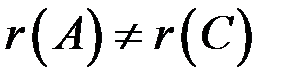 , то система несовместна (решений нет).
, то система несовместна (решений нет).
Пример 7
Исследовать и решить СЛАУр: 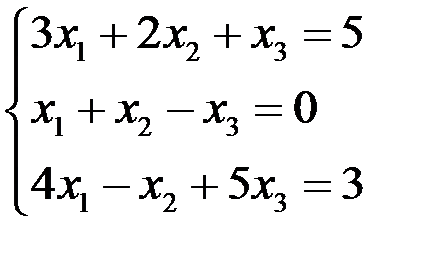 .
.
Решение
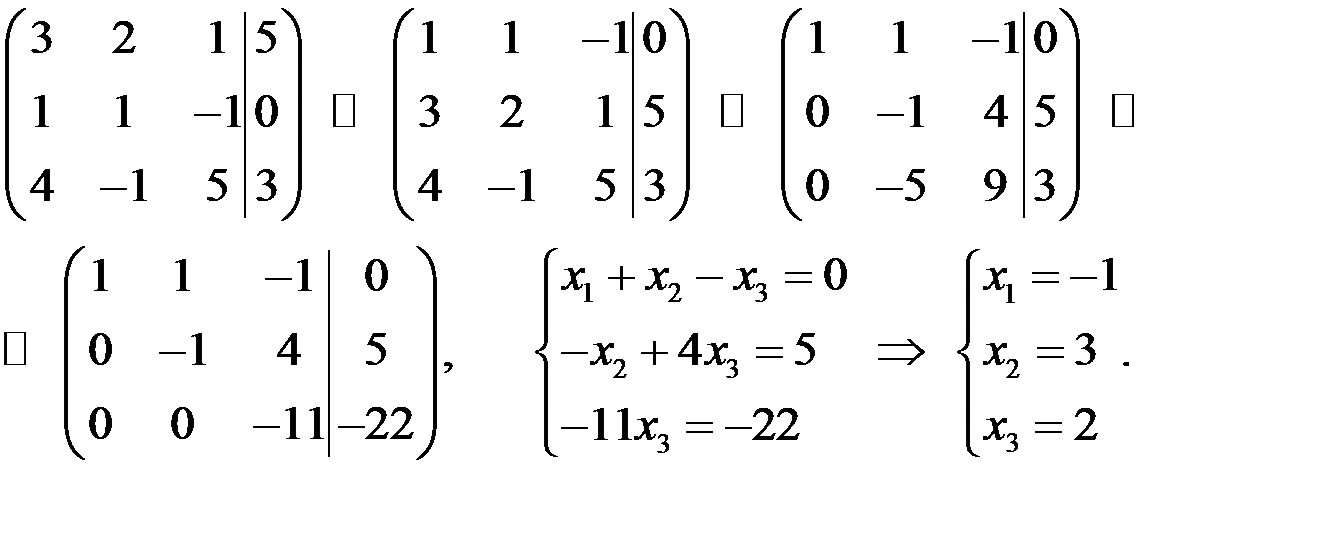
Таким образом, 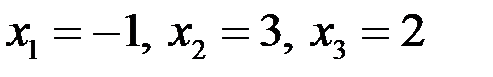 .
.
