Тема 5. Интегральное исчисление функции одной переменной
Краткие теоретические сведения
Функция F(x) называется первообразной функцией функции f(x) на промежутке X, если для любого x из данного промежутка X верно равенство: F¢(x) = f(x).
Неопределенным интеграломотфункции f(x) называется множество всех первообразных функций F(x) + C для функции f(x).
Записывают: 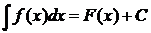 .
.
Основные свойства неопределенного интеграла:
1. 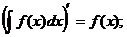
2. 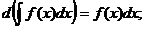
3. 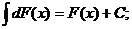
4. 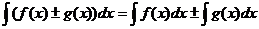 ;
;
5. 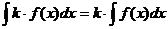 , где k
, где k 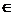 R, k
R, k 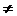 0.
0.
Метод интегрирования подстановкой (заменой переменной): 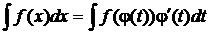 .
.
Метод интегрирования по частям: 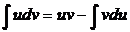 ;
;
Если существует конечный предел суммы 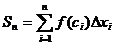 при
при 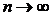 , не зависящей ни от способа разбиения отрезка [a, b] на части, ни от выбора точек
, не зависящей ни от способа разбиения отрезка [a, b] на части, ни от выбора точек  , то этот предел называется определенным интегралом от функции y = f(x) на отрезке [a, b].
, то этот предел называется определенным интегралом от функции y = f(x) на отрезке [a, b].
Обозначается: 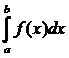 =
= 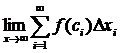 , а – нижний предел, b – верхний предел интегрирования, х – переменная интегрирования, [a, b] – отрезок интегрирования.
, а – нижний предел, b – верхний предел интегрирования, х – переменная интегрирования, [a, b] – отрезок интегрирования.
Основные свойства определенного интеграла:
1) Для любых a, b, c верно 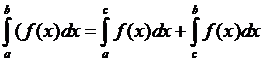 ;
;
2) 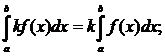
3) 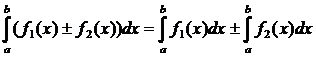
4) Если f(x) £ j(x) на отрезке [a, b] то 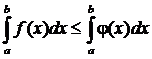
5) Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то: 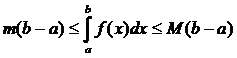 ;
;
6) Теорема о среднем. Если функция f(x) непрерывна на отрезке [a, b], то на
этом отрезке существует точка c такая, что 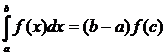 .
.
Формула Ньютона – Лейбница: Если функция F(x) – какая - либо перво-образная от непрерывной функции f(x), то 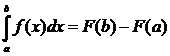 .
.
Метод интегрирования подстановкой (заменой переменной):
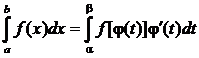 , здесь j(a) = а, j(b) = b.
, здесь j(a) = а, j(b) = b.
Метод интегрирования по частям: 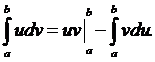
Геометрический смысл определенного интеграла: Определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.
Задания к расчетно-графической работе
Задание 5.1.Найдите неопределенные интегралы.
| Вариант | Вариант | ||
а) 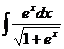 ; б) ; б) 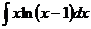 ; в) ; в) 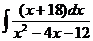 ; г) ; г) 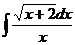 ; д) ; д) 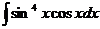 . . | а) 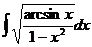 ; б) ; б) 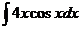 ; в) ; в) 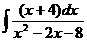 ; г) ; г) 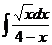 ; д) ; д) 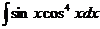 . . | ||
а) 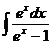 ; б) ; б) 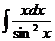 ; в) ; в) 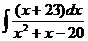 ; г) ; г) 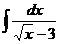 ; д) ; д) 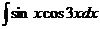 . . | а) 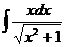 ; б) ; б) 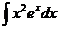 ; в) ; в) 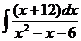 ; г) ; г) 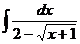 ; д) ; д) 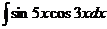 . . | ||
а) 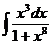 ; б) ; б) 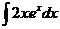 ; в) ; в) 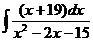 ; г) ; г) 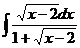 ; д) ; д) 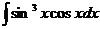 . . | а) 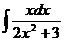 ; б) ; б) 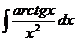 ; в) ; в) 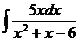 ; г) ; г) 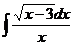 ; д) ; д) 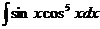 . . | ||
а) 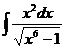 ; б) ; б) 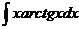 ; в) ; в) 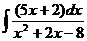 ; г) ; г) 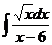 ; д) ; д) 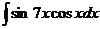 . . | а) 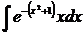 ; б) ; б) 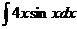 ; в) ; в) 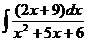 ; г) ; г) 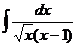 ; д) ; д) 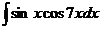 . . | ||
а) 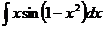 ; б) ; б) 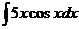 ; в) ; в) 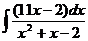 ; г) ; г) 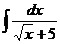 ; д) ; д) 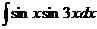 . . | а) 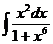 ; б) ; б) 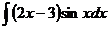 ; в) ; в) 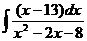 ; г) ; г) 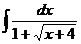 ; д) ; д) 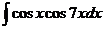 . . |
Задание 5.2. Вычислить площадь фигуры, ограниченной линиями.
| Вариант | Задание | Вариант | Задание |
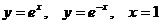 | 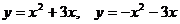 | ||
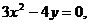 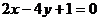 | 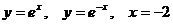 | ||
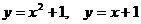 | 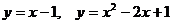 | ||
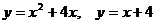 | 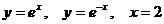 | ||
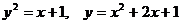 | 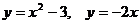 |
Пример выполнения заданий по теме 5
Задание 5.1.Найдите неопределенные интегралы:
а) 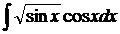 ;
;
б) 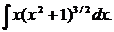 ;
;
в) 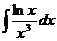 ;
;
г) 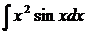 ;
;
д) 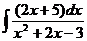 ;
;
е) 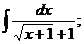
ж) 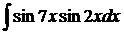 ;
;
Решение.
а) Сделаем замену t = sinx. Тогда dt = cosxdt и:
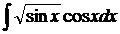 =
= 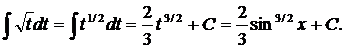
б) Выполним замену: 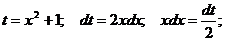 Получаем:
Получаем:
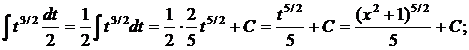
в) Воспользуемся методом интегрирования по частям:
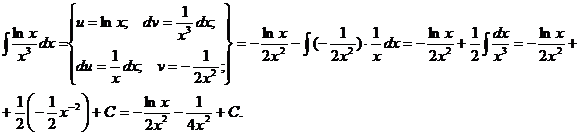
г) Применим метод интегрирования по частям дважды: 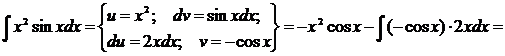
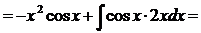
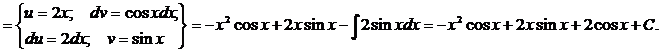 д) Представим дробь
д) Представим дробь 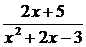 в виде суммы простейших дробей.
в виде суммы простейших дробей.
Так как 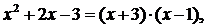 то
то 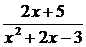 =
= 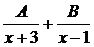 .
.
Тогда 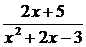 =
= 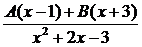 . Откуда следует, что 2x + 5 = A(x – 1) + + B(x + 3). Положим x = -3, тогда -1 = -4A, то есть A =
. Откуда следует, что 2x + 5 = A(x – 1) + + B(x + 3). Положим x = -3, тогда -1 = -4A, то есть A = 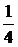 ; Положим x = 1, тогда 7 = 4B, то есть B =
; Положим x = 1, тогда 7 = 4B, то есть B = 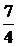 . Следовательно,
. Следовательно, 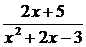 =
= 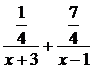 . Тогда
. Тогда 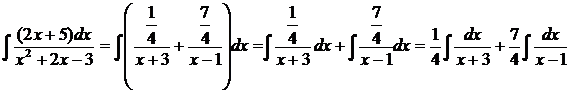 =
=
= 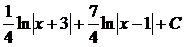
е) Для нахождения данного интеграла воспользуемся подстановкой t = 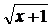 . Тогда
. Тогда 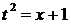 , откуда
, откуда 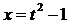 и
и 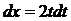 . Таким образом,
. Таким образом, 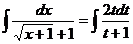 .
.
Так как под знаком интеграла получилась неправильная дробь 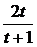 , то разложим неправильную дробь на сумму правильной дроби и многочлена. Выполнив деление числителя на знаменатель, получим:
, то разложим неправильную дробь на сумму правильной дроби и многочлена. Выполнив деление числителя на знаменатель, получим: 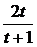 = 2 -
= 2 - 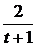 . Тогда
. Тогда 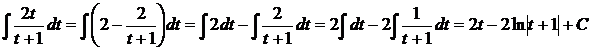 . Сделав обратную замену t =
. Сделав обратную замену t = 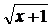 , получим, что
, получим, что 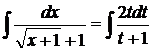 =
= 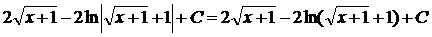 .
.
ж) Для нахождения данного интеграла воспользуемся формулой:
sin 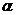 sin
sin 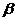 =
= 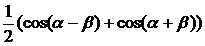 .
.
Тогда:
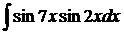 = =
= = 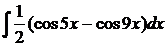 =
= 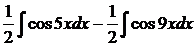 = =
= = 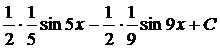
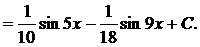
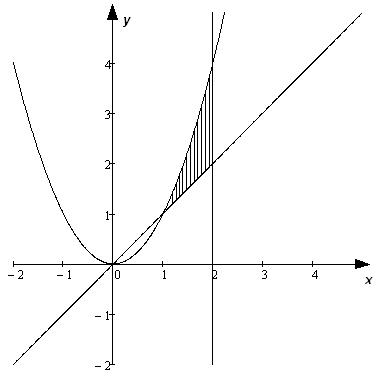
Задание 5.2.Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2.
Решение.
График функции y = x – прямая, являющаяся осью симметрии первого и третьего координатных углов; график функции y = x2 - парабола с вершиной в точке (0;0), а графиком линии x = 2 является прямая, перпендикулярная оси абсцисс и проходящая через точку (2; 0).
Построим графики функций: y = x, y = x2, x = 2.
Искомая фигура заштрихована на рисунке:
Тогда
S 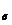 =
= 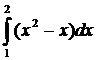
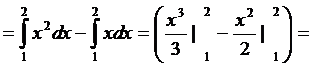
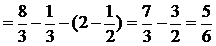 (ед2)
(ед2)
