Необходимое и достаточные условия сходимости ряда.

При рассмотрении рядов возникают две задачи: 1) исследовать ряд на сходимость и 2) зная, что ряд сходится, найти его сумму. Будем решать в основном первую задачу, имеющую теоретический характер. Приведем необходимое условие сходимости рядов.

Если ряд 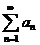сходится, то его общий член стремится к нулю, т.е. 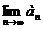=0.

Числовой ряд:

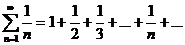
называется гармоническим рядом.

Только невыполнение необходимого условия сходимости позволяет делать определённый вывод, а его выполненине, как в данном случае 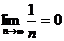, не позволяет судить о сходимости.

Признаки сходимости рядов

Перейдем теперь к рассмотрению некоторых достаточных условий сходимости рядов с неотрицательными членами.

Для того чтобы, ряд 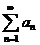с неотрицательными членами сходился, необходимо и достаточно, чтобы последовательность частичных сумм этого ряда была ограничена.

Это значит, что последовательность его частичных сумм имеет предел. Всякая сходящаяся последовательность является ограниченной.

Установим ряд признаков, позволяющих сделать вывод о сходимости (расходимости) рассматриваемого ряда.

Признак сравнения.

Пусть даны два ряда с неотрицательными членам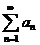и и 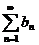и для всех n выполняется неравенство 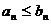. Тогда: из сходимости ряда 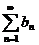следует сходимость ряда 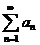, а из расходимости ряда 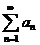следует расходимость ряда .

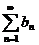Признак Даламбера (Даламбер Жан Лерон (1717-1783)-французский математик, механик и философ-просветитель).

Пусть дан ряд 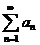с положительными членами и существует предел 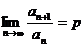. Тогда: а) при 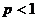ряд сходится; б) при 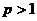ряд расходится.

Интегральный признак.

Пусть дан ряд 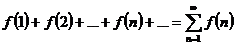, члены которого являются значениями некоторой функции 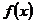, положительной, непрерывной и убывающей на полуинтервале .

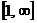Тогда, если 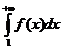сходится, то сходится и ряд ;

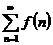если же 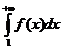расходится, то ряд 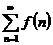также расходится.

Гармонический ряд:

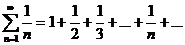
расходится, так как .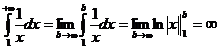

До сих пор мы рассматривали ряды с неотрицательными членами. Ряды с неположительными членами отличаются от соответствующих рядов с неотрицательными членами только множителем (-1), поэтому вопрос об их сходимости решается аналогично.

Перейдем теперь к рассмотрению знакочередующихся рядов, члены которых имеют чередующиеся знаки. Для удобства будем считать, что первый член такого ряда положителен. Тогда знакочередующийся ряд можно записать в ви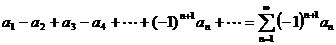де:

, где .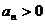

Для знакочередующихся рядов имеет место следующий очень простой достаточный признак сходимости.

ПризнакЛейбница.

Если абсолютные величины членов знакочередующегося ряда монотонно убывают: 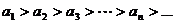и общий член ряда стремится к нулю 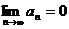, то ряд сходится.

Рассмотрим теперь ряды с членами произвольных знаков. Такие ряды называются знакопеременными рядами.

Возьмем какой-нибудь знакопеременный ряд

,

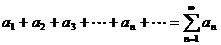где числа 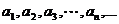могут быть как положительными, так и отрицательными, причем расположение положительных и отрицательных членов в ряде произвольно.