Теории вероятностей и математическая статистика
Теории вероятностей и математическая статистика
Случайные события
Теория вероятностей изучает закономерности массовых, случайных явлений. Одним из основных понятий теории вероятностей является понятие случайного события.
Событием называется всякий факт, который в результате опыта (испытания) может произойти или не произойти.
Примеры событий: получение прибыли при заключении сделки, отказ технического устройства за время его работы, искажение информации при передаче сообщения, получение качественного или бракованного изделия при его изготовлении.
Достоверным называется событие, которое при испытании обязательно произойдет. Обозначают достоверное событие латинской буквой U.
Невозможным называется событие, которое при испытании заведомо не произойдет. Это событие обозначают буквой V.
Случайным называется событие, которое при испытании может произойти или не произойти. Обозначаются случайные события большими буквами латинского алфавита: A, B, C, . . . .
Равновозможными называются случайные события, которые могут произойти с одинаковой возможностью.
Два события называют совместными, если появление одного из них не исключает появления другого. Если появление одного события исключает появление другого, то события несовместны.
Несколько событий называются А1, А2,…, Аn называют попарно несовместными, если появление каждого из них исключает появление любого из остальных.
События А1, А2,…, Аn образуют полную группу событий, если они попарно несовместны, и в результате опыта одно из них обязательно произойдет.
Операции над событиями определяют правила действий с событиями и позволяют выражать одни события через другие.
 Суммой (объединением) событий А и В называется событие С=А+В (С=АÈВ), состоящее в том, что произойдет хотя бы одно из них ( или А, или В, или оба) . На диаграмме (рис 1.2.) событию С соответствует заштрихованная область С, представляющая объединение областей А и В. Аналогично, суммой нескольких событий А1, А2,…, Аn называется событие С, состоящее в том, что произойдет хотя бы одно из событий Аi, i=
Суммой (объединением) событий А и В называется событие С=А+В (С=АÈВ), состоящее в том, что произойдет хотя бы одно из них ( или А, или В, или оба) . На диаграмме (рис 1.2.) событию С соответствует заштрихованная область С, представляющая объединение областей А и В. Аналогично, суммой нескольких событий А1, А2,…, Аn называется событие С, состоящее в том, что произойдет хотя бы одно из событий Аi, i= 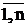 . Если события А1, А2,…, Аn образуют полную группу, то их сумма равна достоверному событию:
. Если события А1, А2,…, Аn образуют полную группу, то их сумма равна достоверному событию: 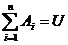 .
.
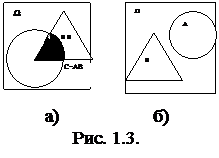
Произведением (пересечением) событий А и В называется событие С=А×В (С=АÇВ), состоящее в совместном появлении событий А и В. На рис 1.3.а событие С представлено пересечением областей А и В. Если А и В – несовместные события, то их произведение - невозможное событие , т. е. А×В=V (рис. 1.3.б).
Произведение событий А1, А2,…, Аn – это событие С, состоящее в совместном появлении всех событий Аi, i= 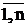 : С=
: С= 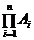 . Произведения попарно несовместных событий А1, А2,…, Аn – невозможные события: Аi×Аj=V, для любого i¹j.
. Произведения попарно несовместных событий А1, А2,…, Аn – невозможные события: Аi×Аj=V, для любого i¹j.
 Противоположным событием
Противоположным событием 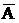 для события А называется событие, состоящее в том, что событие А не произошло.
для события А называется событие, состоящее в том, что событие А не произошло.
Свойства операций над событиями.
1. Переместительные свойства: А+В=В+А, А·В=В·А.
2. Сочетательные свойства: (А+В)+С=А+(В+С), (АВ)С=А(ВС).
3. Распределительное свойство: А(В+С)=АВ+АС.
4. Из определений операций над событиями следуют свойства:
А+А=А; А+U=U; А+V=А; А·А=А; А·U=А; А·V=V.
5 . Из определения противоположного события следует, что:
А+ 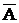 =U; А×
=U; А× 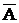 =V;
=V; 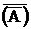 =А;
=А; 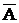 =V;
=V; 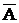 =U; U+V=U; U×V=V.
=U; U+V=U; U×V=V.
Вероятность - это количественная мера возможности появления случайного события А и обозначается она Р(А).
Классическое определение вероятности.События, составляющие при данном испытании полную группу попарно несовместных, равновозможных событий, называют элементарными случаями. Те из элементарных случаев, при которых наступает событие А, называют благоприятствующими событию А.
Вероятностью события А называют отношение числа благоприятствующих элементарных случаев к общему числу всех элементарных случаев. Вероятность определяется формулой
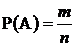 , (1.7)
, (1.7)
где m – число элементарных случаев, благоприятствующих событию А,
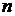 ‑ число всех возможных элементарных случаев.
‑ число всех возможных элементарных случаев.
Пусть проводится опыт, в результате которого могут наступить те или иные события. Если эти события образуют полную группу попарно несовместных и равновозможных событий, то говорят, что опыт обладает симметрией возможных исходов и сводится к "схеме случаев". Для опытов, которые сводятся к схеме случаев, применима классическая формула вероятности.
ПримерВ лотерее разыгрывается 1000 билетов, среди которых 5 выигрышных. Определить вероятность того, что при покупке одного билета будет получен выигрыш.
4Элементарным событием этого опыта является покупка билета. Каждый билет лотереи неповторим, так как имеет свой номер, и купленный билет не возвращается обратно. Событие А заключается в том, что куплен выигрышный билет. При покупке одного из 1000 билетов всевозможных исходов опыта будет 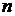 =1000, исходы образуют полную группу несовместных событий. Число исходов, благоприятных событию А, равно
=1000, исходы образуют полную группу несовместных событий. Число исходов, благоприятных событию А, равно 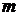 =5. Вероятность получить выигрыш, купив один билет, равна Р(А) =
=5. Вероятность получить выигрыш, купив один билет, равна Р(А) = 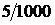 = 0.005.3
= 0.005.3
Для непосредственного подсчета вероятностей удобно применять формулы комбинаторики. Рассмотрим это на примере задачи выборочного контроля.
ПримерПусть имеется партия из 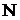 изделий, среди них есть
изделий, среди них есть 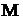 бракованных. Для контроля отбирается часть из
бракованных. Для контроля отбирается часть из 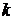 изделий. Какова вероятность того, что среди отобранных изделий будет ровно
изделий. Какова вероятность того, что среди отобранных изделий будет ровно 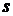 бракованных?
бракованных?
4 Число всех элементарных случаев 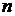 – это число способов, которыми можно отобрать
– это число способов, которыми можно отобрать 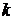 изделий из партии содержащей
изделий из партии содержащей 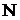 изделий, оно равно числу сочетаний из
изделий, оно равно числу сочетаний из 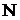 элементов по
элементов по 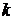 :
: 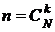 . Число элементарных случаев, благоприятствующих событию А согласно правилу умножения комбинаторики, будет
. Число элементарных случаев, благоприятствующих событию А согласно правилу умножения комбинаторики, будет 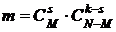 . Тогда искомая вероятность
. Тогда искомая вероятность 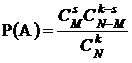 .
.
Например, пусть 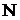 =100,
=100, 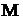 =10,
=10, 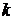 =10,
=10, 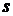 =1. Тогда вероятность того, что среди отобранных 10 изделий будет ровно одно бракованное, равна
=1. Тогда вероятность того, что среди отобранных 10 изделий будет ровно одно бракованное, равна
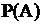 =
= 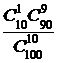 =
= 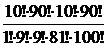 =
= 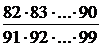 » 0.408. 3
» 0.408. 3
Геометрическое определение вероятности. Это определение вероятности обобщает классическое определение на случай, когда число элементарных случаев безконечно, что приводит к неопределенности в классической формуле.
Геометрической вероятностью события А называется отношение меры 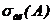 области, благоприятствующей появлению события, к мере
области, благоприятствующей появлению события, к мере 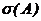 всей области:
всей области: 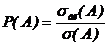 (1.10)
(1.10)
Если области представляют собой а) длины отрезков 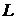 , б) площади фигур
, б) площади фигур 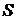 , в) объемы пространственных фигур
, в) объемы пространственных фигур 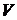 , то геометрические вероятности соответственно равны:
, то геометрические вероятности соответственно равны:
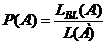 ;
; 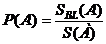 ;
; 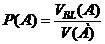 . (1.11)
. (1.11)
Пример . Рекламные объявления развешены с интервалом в 10 метров вдоль торгового ряда. Широта обзора у некоторого покупателя составляет 3 метра. Какова вероятность того, что он не заметит рекламу, если он движется перпендикулярно торговому ряду и пересечь ряд может в любой точке?
 4Участок торгового ряда, расположенный между двумя объявлениями, можно представить как отрезок прямой АВ (рис. 1.6).Чтобы покупатель заметил объявления, он должен пройти через отрезки АС или ДВ, равные 3м. Если же он пересечет торговый ряд в одной из точек отрезка СД, длина которого 4м, то он не заметит рекламы. Вероятность этого события будет Р =
4Участок торгового ряда, расположенный между двумя объявлениями, можно представить как отрезок прямой АВ (рис. 1.6).Чтобы покупатель заметил объявления, он должен пройти через отрезки АС или ДВ, равные 3м. Если же он пересечет торговый ряд в одной из точек отрезка СД, длина которого 4м, то он не заметит рекламы. Вероятность этого события будет Р = 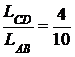 =0.4. 3
=0.4. 3
Событие А называется независимым от события В, если его вероятность не зависит от появления или не появления В, в противном случае событие А называют зависимым от события В.
Вероятность события А, вычисленная в предположении, что событие В произошло, называется условной вероятностью, обозначается 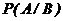 и вычисляется:
и вычисляется:
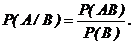
Вероятность появления суммы двух несовместных событий равна сумме вероятностей этих событий
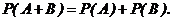
Вероятность появления суммы попарно несовместных событий равна сумме вероятностей этих событий:
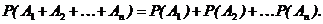
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
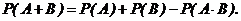
Формула (2.4.) может быть обобщена на любое конечное число совместных событий. Например, для трех совместных событий:
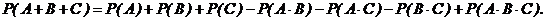
Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
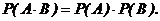
Вероятность появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
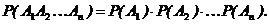
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, при условии, что первое событие произошло:
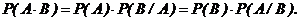
Вероятность совместного появления нескольких зависимых событий равна произведению вероятностей одного из них на условные вероятности всех последующих событий, вычисленных в предположении, что все предыдущие события 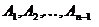 наступили.
наступили.
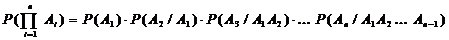
Вероятность наступления события А, состоящего в появлении хотя бы одного из событий 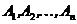 , равна разности между единицей и вероятностью произведения всех противоположных событий
, равна разности между единицей и вероятностью произведения всех противоположных событий 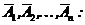
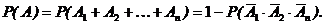
Формула полной вероятности. Формулы гипотез (Бейеса).
Пусть событие А может наступить при появлении одного из несовместных событий 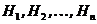 , образующих полную группу и называемых гипотезами. Вероятности гипотез
, образующих полную группу и называемых гипотезами. Вероятности гипотез 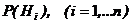 предполагаются известными, причем
предполагаются известными, причем 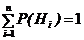 . Тогда вероятность появления события А равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А, вычисленную в предположении, что произошла i – тая гипотеза, т.е.
. Тогда вероятность появления события А равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А, вычисленную в предположении, что произошла i – тая гипотеза, т.е.
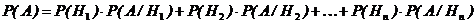 =
=
= 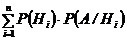
Это равенство называют формулой полной вероятности.
Если событие А произошло, то вероятности гипотез изменятся и могут быть переоценены по формулам Бейеса:
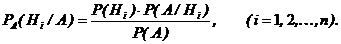
где 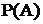 вычисляется в соответствии с формулой погной вероятности.
вычисляется в соответствии с формулой погной вероятности.
Пример. В продажу поступили однотипные изделия с трех заводов. Продукция первого завода содержит 20% изделий с дефектом, второго – 8% и третьего 15%. Какова вероятность приобрести изделие с дефектом, если в магазин поступило 30% изделий первого завода, 50% изделий второго завода и 20% - третьего?
4Обозначим:
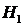 ={изделие произведено первым заводом},
={изделие произведено первым заводом}, 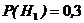 ;
;
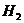 ={изделие произведено вторым заводом},
={изделие произведено вторым заводом}, 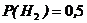 ;
;
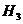 ={изделие произведено третьим заводом},
={изделие произведено третьим заводом}, 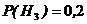 ;
;
А= {купленное изделие имеет дефект}.
Событие А может произойти совместно с одной из гипотез Н 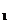 , Н
, Н  или Н
или Н 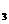 , причем
, причем
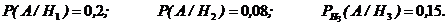
Вероятность события А можно вычислить по формуле полной вероятности:
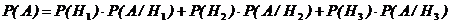 =
=
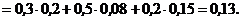 3
3
Формула Бернулли
Пусть опыт состоит в проведении серии 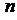 испытаний, в каждом из которых событие А может произойти с вероятностью Р(А)=р или не произойти с вероятностью Р(
испытаний, в каждом из которых событие А может произойти с вероятностью Р(А)=р или не произойти с вероятностью Р( 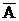 ) = 1 - Р(А) = 1 ‑ р = q. Если результат каждого испытания не зависит от исхода других, то испытания называются независимыми повторными испытаниями. Событие А называют простым событием. Событие ‑{ появление простого события А ровно
) = 1 - Р(А) = 1 ‑ р = q. Если результат каждого испытания не зависит от исхода других, то испытания называются независимыми повторными испытаниями. Событие А называют простым событием. Событие ‑{ появление простого события А ровно 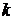 раз в
раз в 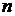 независимых испытаниях} ‑называют сложным событием и обозначают
независимых испытаниях} ‑называют сложным событием и обозначают 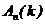 .
.
Опыт, удовлетворяющий перечисленным условиям, называют схемой испытаний Бернулли или схемой независимых испытаний.
Цель опыта: определить вероятность 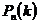 сложного события
сложного события 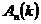 , заключающегося в том, что в
, заключающегося в том, что в 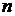 независимых испытаниях простое событие А появится ровно
независимых испытаниях простое событие А появится ровно 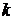 раз и не появится
раз и не появится 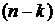 раз.
раз.
Эта вероятность определяется формулой Бернулли:
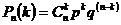 ,
,
где 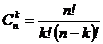 ‑ биномиальные коэффициенты.
‑ биномиальные коэффициенты.
Всего сложных вероятностей в схеме испытаний Бернулли всегда 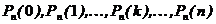 .
.
Сумма сложных вероятностей равна сумме вероятностей полной группы попарно несовместных событий и описывает вероятность достоверного события, равную единице:

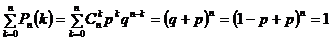 .
.
ПримерВероятность того, что в течение рабочего дня произойдет сбой в поставке сырья на производство, равна 0.8. Определить вероятности того, что в течение рабочей недели (5 дней):
1) три рабочих дня не будет сбоя в поставке сырья;
2) сбой в поставках будет в трех рабочих днях;
3) сбой будет менее чем в трех рабочих днях;
4) днях.
Простое событие А = {нет сбоя в поставках сырья в течение одного рабочего дня}, Р(А)=р=0.8. Противоположное событие 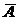 ={произошел сбой в поставках сырья в течение рабочего дня},
={произошел сбой в поставках сырья в течение рабочего дня},
Р( 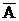 ) = 1‑ р = q = 0.2.
) = 1‑ р = q = 0.2.
1) Сложное событие В={ровно три рабочих дня не будет сбоя в поставке сырья}, его вероятность вычисляем по формуле Бернулли:
Р(В) = 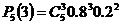 =
= 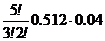 =
= 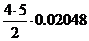 =0.2048
=0.2048
2) Событие С= {сбой в поставках будет в трех рабочих днях},
Р(С) = 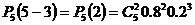 =
= 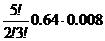 =0.0512
=0.0512
3) Событие D= {сбой в поставках будет менее чем в трех рабочих днях} равно сумме сложных событий: {сбоя не будет ни в одном дне}, {сбой будет в одном дне}, {сбой будет в двух днях}. Эти события несовместны, поэтому:
P(D) = 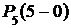 +
+ 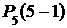 +
+ 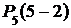 =
= 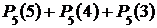 =
=
= 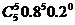 +
+ 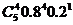 +
+ 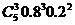 = 0.512(0.64+0.8+0.4) = 0.94208.
= 0.512(0.64+0.8+0.4) = 0.94208.
Если число испытаний достаточно велико, то при вычислении вероятностей сложных событий по формуле Бернулли возникают вычислительные проблемы, связанные с громоздкостью вычислений и с неизбежной потерей точности расчетов.
Например, в рамках условий примера 3.1 вероятность того, что за год работы предприятия (288 рабочих дней) сбой в поставках сырья произойдет в 48 рабочих днях, определяется формулой: 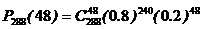 =
= 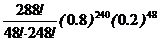 . Получить по этой формуле результат с допустимой точностью практически невозможно.
. Получить по этой формуле результат с допустимой точностью практически невозможно.
Для определения вероятностей сложных событий, подчиняющихся схеме независимых испытаний, существуют асимптотические формулы, позволяющие достаточно точно вычислить сложные вероятности в случае, если 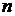 велико.
велико.
Локальная теорема Лапласа. Если вероятность наступления события А в каждом из 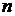 независимых испытаний равна
независимых испытаний равна 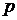 и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность
и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность 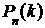 того, что в
того, что в 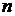 испытаниях событие А наступит
испытаниях событие А наступит 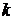 раз, приближенно равна (тем точнее, чем больше
раз, приближенно равна (тем точнее, чем больше 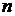 )
)
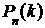 »
» 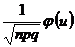 , где
, где 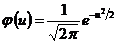 ,
, 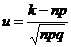 .
.
Существуют специальные таблицы (см. приложения), которые содержат значения функции 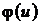 для положительных значений аргумента
для положительных значений аргумента 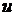 . Функция
. Функция 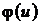 четная (
четная ( 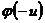 =
= 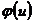 ) и ее значения при отрицательных значениях аргумента определяют по тем же таблицам.
) и ее значения при отрицательных значениях аргумента определяют по тем же таблицам.
Пример .Вероятность того, что сошедшая с конвейера деталь стандартная, равна 0.9. Деталь тут же проверяется ОТК. За смену с конвейера сходит 400 деталей. Найти вероятность того, что объем продукции, принятой ОТК за смену, составит ровно 356 деталей.
4 Из условия задачи следует, что данные испытания подчиняются схеме испытаний Бернулли: опыты независимы друг от друга, исход опыта – простое событие (есть брак или нет брака), вероятность простого события в каждом опыте одинакова и отлична от нуля или единицы. Число испытаний 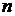 =400 велико, т. е. удовлетворяются все условия локальной теоремы Лапласа. Сложная вероятность
=400 велико, т. е. удовлетворяются все условия локальной теоремы Лапласа. Сложная вероятность 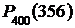 определяется по формуле:
определяется по формуле:
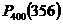 »
» 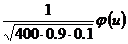 , где
, где 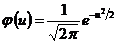 ,
,
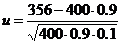 =
= 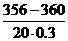 =
= 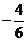 » ‑ 0.667.
» ‑ 0.667.
По таблицам приложения определяем значение функции 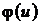 , учитывая четность функции:
, учитывая четность функции: 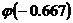 =
= 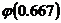 » 0.3188. Искомая вероятность
» 0.3188. Искомая вероятность
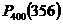 »0.3188/6 » 0.0531. 3
»0.3188/6 » 0.0531. 3
Интегральная теорема Лапласа. Если вероятность наступления события А в каждом из 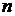 независимых испытаний равна
независимых испытаний равна 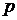 и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, что в
и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, что в 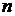 испытаниях событие А наступит не менее
испытаниях событие А наступит не менее 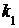 и не более
и не более 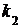 раз, приближенно равна (тем точнее, чем больше
раз, приближенно равна (тем точнее, чем больше 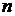 )
)
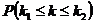 =
= 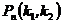 »
» 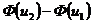 ,
,
где 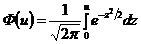 ‑ функция Лапласа,
‑ функция Лапласа, 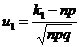 ,
, 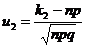 .
.
Функция Лапласа представляет собой интеграл с переменным верхним пределом, не берущийся в рамках элементарных функций. Для вычисления его при заданном значении переменной существуют таблицы (см. приложение), в которых приведены значения интеграла Лапласа для положительных значений аргумента 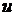 Î[0, 5]. Для
Î[0, 5]. Для 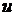 >5 полагают значения функции Лапласа постоянными и равными
>5 полагают значения функции Лапласа постоянными и равными 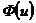 = 0.5. Интеграл Лапласа – функция нечетная (
= 0.5. Интеграл Лапласа – функция нечетная ( 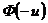 =
= 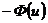 ), и для
), и для 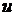 <0 используют те же таблицы с
<0 используют те же таблицы с 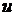 > 0, но значению
> 0, но значению 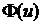 приписывают знак минус.
приписывают знак минус.
Понятие случайной величины
Случайная величина (СВ) - это переменная величина, принимающая свои значения в зависимости от случая, с некоторой вероятностью.Случайные величины бывают дискретные и непрерывные.
Дискретной называется СВ, принимающаяотдельные, изолированные значения, которые можно перенумеровать (ихчисло может быть конечным или бесконечным).
Непрерывной называется СВ, значения которой сплошь заполняют некоторый промежуток (конечный или бесконечный).
Например, число пассажиров, перевозимых городским транспортом, число бракованных изделий среди изготовленных, число зёрен в колосе пшеницы, число студентов не посещающих занятия являются дискретными СВ, а случайные ошибки взвешивания, время безотказной работы кассового аппарата ‑ непрерывными СВ.
Полностью охарактеризовать СВ можно законом ее распределения.
Закон распределения СВ Х - это есть соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Их числовые характеристики
Биномиальное распределение
СВ Х распределена по биномиальному закону, если она принимает значения 0, 1, 2, …, n, а соответствующие вероятности вычисляются по формуле Бернулли:
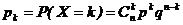 , (5.1
, (5.1
где 0 < p < 1, q=1 - p, k=0, 1, 2, …, n.
Такая СВ выражает число появлений события А в п независимых испытаниях, проводимых в одинаковых условиях.
| Ряд распределения имеет вид: | ||||||
| хi=k | … | i | n | |||
| P(X=k) | 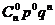 | 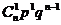 | 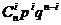 | 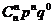 |
А числовые характеристики равны:
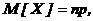 D[X]=npq.
D[X]=npq.
ПримерТри конкурирующие фирмы работают независимо друг от друга. Вероятность обанкротиться для каждой из них равна 0.1. Составить закон распределения СВ Х – числа обанкротившихся фирм. Найти математическое ожидание и дисперсию Х.
4Дискретная СВ X - число обанкротившихся фирм имеет следующие возможные значения: x1=0 (ни одна фирма не обанкротилась), x2=1 (обанкротилась одна фирма), x3=2 (две обанкротились) и x4=3(обанкротились все три). Банкротства фирм независимы друг от друга, поэтому применима формула Бернулли ( n=3, k=0, 1, 2, 3; p=0,1, q=1 ‑ 0,1= 0,9 ), следовательно,
P(X=0)=P3(0)=q3=0,93=0,729; P(X=1)=P3(1)= 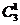 pq2=3´0,1´0,9=0,243;
pq2=3´0,1´0,9=0,243;
P(X=2)=P3(2)= 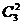 p2q=3´(0,1)2´(0,9)=0,027; P(X=3)=P3(3)=p3=0,13=0,001.
p2q=3´(0,1)2´(0,9)=0,027; P(X=3)=P3(3)=p3=0,13=0,001.
Контроль: 0,729+0,243+0,027+0,001=1.
` Закон распределения Х имеет вид:
| хi=k | ||||
| P(X=k) | 0,729 | 0,243 | 0,027 | 0,001 |
M[X]= 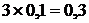 ; D[X]=
; D[X]= 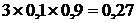 . 3
. 3
Распределение Пуассона
СВ Х распределена по закону Пуассона, если онапринимает целые неотрицательные значения: 0, 1, 2, …, k, …, вероятности которых можно вычислить по формулам:
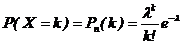 ,
,
где k – число появлений событияАв n независимыхиспытаниях ( 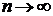 ),
), 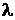 (
( 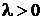 )‑ параметр распределения, который равен среднему числу появления события А в n испытаниях. Если вероятность появления события А в каждом испытании одинакова и равна р, то
)‑ параметр распределения, который равен среднему числу появления события А в n испытаниях. Если вероятность появления события А в каждом испытании одинакова и равна р, то 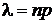 .
.
Распределение Пуассона является предельным для биномиального распределения, когда число испытаний n достаточно велико, а вероятность р появления события в каждом испытании мала (порядка 1/n).
Ряд распределения СВ Х , распределенной по закону Пуассона, имеет вид:
| х | … | n | … | |||
| рk | 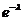 | 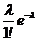 | 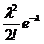 | … | 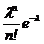 | … |
Математическое ожидание и дисперсия соответственно равны:
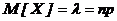 , D
, D 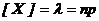 .
.
Пример.На телефонную станцию в течение часа поступают в среднем 30 вызовов. Найти вероятность того, что в течение минуты поступает не более двух вызовов.
4Математическое ожидание числа вызовов за минуту равно 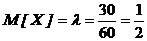 . Вероятность того, что в течение данной минуты будет получено не более двух вызовов, равна сумме вероятностей того, что в течение данной минуты будет либо 0, либо 1, либо 2 вызова. Поэтому искомая вероятность:
. Вероятность того, что в течение данной минуты будет получено не более двух вызовов, равна сумме вероятностей того, что в течение данной минуты будет либо 0, либо 1, либо 2 вызова. Поэтому искомая вероятность:
P(k£2) = p(X=0)+P(X=1)+P(X=2)= = 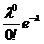 +
+ 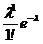 +
+ 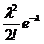 =
= 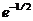 (1+1/2+
(1+1/2+ 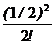 )»0,98. 3
)»0,98. 3
Равномерное распределение
СВ Х подчинена равномерному закону распределения, если ее плотность распределения вероятностей имеет вид:
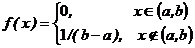 .
.
График плотности равномерного распределения f(x) изображен на рис.5.1.
Интегральная функция распределения F(x) равна: 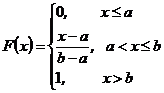 ,
,
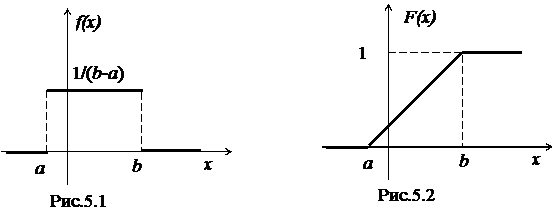 |
ее график изображен на рис. 5.2.
Математическое ожидание, дисперсия и среднее квадратичное отклонение соответственно равны:
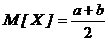 ; D
; D 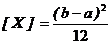 ;
; 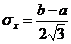 .
.
Вероятность попадания Х в заданный интервал значений 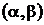 определяется:
определяется: 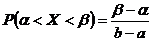 .
.
Показательное распределение
Непрерывная СВ Х распределена по показательному (экспоненциальному) закону, если ее плотность распределения вероятностей имеет вид:
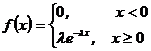 ,
,
где l - параметр распределения.
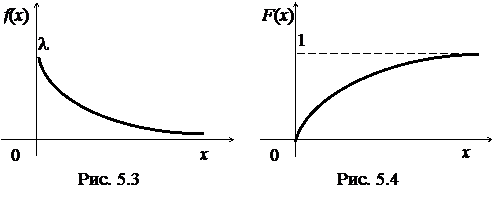
Кривая плотности распределения f(x)изображена на рис.5.3. Интегральная функция распределения равна
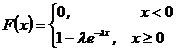 ,
,
ее график показан на рис 5.4.
 |
Математическое ожидание, дисперсия и среднее квадратичное соответственно равны:
M[X]=1/l; D[X]=1/l2; sх=1/l;
а вероятность попадания Х в заданный интервал значений 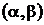 определяется следующим образом:
определяется следующим образом: 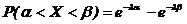 .
.
Пример.СВ Т—время безотказной работы телевизора - имеет показательное распределение. Определить вероятность того, что время безотказной работы телевизора будет не меньше 600 часов, если среднее время работы его 400 часов.
4 По условию задачи математическое ожидание СВ Т равно 400 часов. Искомая вероятность
P(T ³ 600 )= 1- P(T<600 )= 1- F(600)=1-(1-e-600/400 )=e-1,5 » 0,2231. 3
Нормальное распределение
СВ Х подчинена нормальному закону распределения,если ее плотность распределения вероятностей имеет вид:
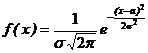 ,
,
где a ‑ математическое ожидание, 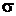 ‑ среднее квадратичное отклонениеХ.
‑ среднее квадратичное отклонениеХ.
Интегральная функция нормального распределения имеет вид
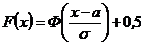 ;
;
где 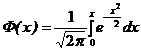 - функция Лапласа, или интеграл вероятностей.
- функция Лапласа, или интеграл вероятностей.
Основные свойства функции Лапласа:
1) F(0) = 0;
2) 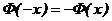 (нечетная функция);
(нечетная функция);
3) F(¥)=0,5
Таблица значений функции F(х) для 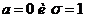 приведена в приложении, поскольку она является нечетной, то для отрицательных значений х пользуются теми же таблицами, что и для положительных.
приведена в приложении, поскольку она является нечетной, то для отрицательных значений х пользуются теми же таблицами, что и для положительных.
Вероятность попадания Х в заданный интервал значений 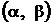 :
:
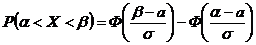 ,
,
Вероятность того, что абсолютная величина отклонения 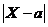 нормальной СВ Х от ее математического ожидания меньше положительного числа d, определяется выражением:
нормальной СВ Х от ее математического ожидания меньше положительного числа d, определяется выражением:
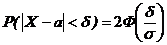 .
.
В частности, при а=0, P(êХ ê<d) =2F(d/s).
Если в равенстве 5.17. 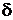 взять
взять 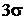 , получим так называемое «правило трёх сигм», которое является одним из необходимых условий того, что СВ имеет нормальный закон распределения. В самом деле,
, получим так называемое «правило трёх сигм», которое является одним из необходимых условий того, что СВ имеет нормальный закон распределения. В самом деле, 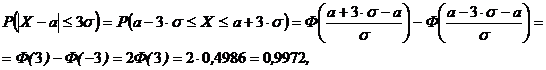
т.е. отклонение нормальной СВ от своего математического ожидания а на величину, равную 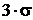 является событием практически достоверным.
является событием практически достоверным.
 Асимметрия, эксцесс, мода и медиана нормального распределения соответственно равны:
Асимметрия, эксцесс, мода и медиана нормального распределения соответственно равны:
аs=0, еk=0, Mo=a, Me=a, где a=M[X].
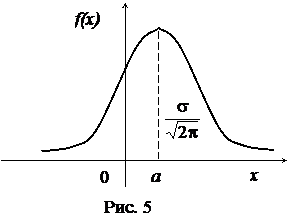
График плотности вероятности нормального распределения (рис.5) называют нормальной кривой (кривой Гаусса).
Теории вероятностей и математическая статистика
Случайные события
Теория вероятностей изучает закономерности массовых, случайных явлений. Одним из основных понятий теории вероятностей является понятие случайного события.
Событием называется всякий факт, который в результате опыта (испытания) может произойти или не произойти.
Примеры событий: получение прибыли при заключении сделки, отказ технического устройства за время его работы, искажение информации при передаче сообщения, получение качественного или бракованного изделия при его изготовлении.
Достоверным называется событие, которое при испытании обязательно произойдет. Обозначают достоверное событие латинской буквой U.
Невозможным называется событие, которое при испытании заведомо не произойдет. Это событие обозначают буквой V.
Случайным называется событие, которое при испытании может произойти или не произойти. Обозначаются случайные события большими буквами латинского алфавита: A, B, C, . . . .
Равновозможными называются случайные события, которые могут произойти с одинаковой возможностью.
Два события называют совместными, если появление одного из них не исключает появления другого. Если появление одного события исключает появление другого, то события несовместны.
Несколько событий называются А1, А2,…, Аn называют попарно несовместными, если появление каждого из них исключает появление любого из остальных.
События А1, А2
