Экономический смысл производной

Рассмотрим понятия, иллюстрирующие экономический смысл производной.

Пусть y(x) -функция, характеризующая, например, издержки производства, где x - количество выпускаемой продукции. Тогда отношение y(x)/x описывает средние издержки, приходящиеся на одно изделие. Средняя величина обозначается Ay или Af (от английского "average".) Среднее приращение, средний прирост, средняя скорость изменения определяется отношением ∆ y/∆ x. Производная

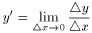
выражает предельные (маргинальные от английского "marginal") издержки производства. Величину Mf(x) = y' называют мгновенным приростом или мгновенной скоростью изменения y. Аналогично можно определить предельную выручку, предельный доход, предельную полезность и другие предельные величины.

Определение 5.Отношение 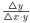называется темпом прироста функции y. Отношение 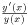называется мгновенным темпом прироста.

Обычно степень влияния одной переменной на другую, зависимую от нее, измеряют производной данной функции. Однако часто экономистов интересуют относительные изменения величин. Например, если маленькое яблоко подорожало на 2,5 рубля, то при этом большое, скажем, на 5. В тоже время, если яблоки подорожали в 1,5 раза, то в 1,5 раза дороже стало и маленькое, и большое яблоко, и килограмм, и вагон яблок. Поэтому для анализа относительных изменений вместе с понятием производной используют понятие эластичности.

Определение 6 (эластичность).Эластичностью функции E_x(y) называется величина

E_x(y) = lim_{∆x→ 0} (∆y/y: ∆x/x) = x/ylim_{∆x→ 0} ∆y/∆x = x/y· y'.

Определение 7.Будем говорить, что y(x) эластична в точке x, если |E_x(y)|>1, y(x) неэластична, если |E_x(y)| <1, и нейтральна, если |E_x(y)| = 1.

Рассмотрим некоторые свойства эластичности.

1. Эластичность - безразмерная величина, ее значение не зависит от того, в каких единицах измерены аргумент и функция. Если u = Ax, v = By, то E_u(v) = (dv/du)· u/v=(B/A)· (dy/dx)· (Ax/By) = E_x(y);

2. Эластичности взаимно обратных функций - взаимно обратные величины

E_y(x) = (dx/dy)·(y/x) = 1/E_x(y).

3. Эластичность функции равна произведению независимой переменной x на темп изменения функции T_y = (ln y)' = y'/y, то есть

E_x(y) = xT_y.

4. Эластичность произведения (частного) двух функций равна сумме (разности) эластичностей этих функций:

E_x(uv) = E_x(u)+E_x(v), E_x(u/v) = E_x(u)-E_x(v).

5. Из последнего свойства следуют формулы

E_x(xy) = E_x(x)+E_x(y) = 1+E_x(y)

отсюда, если E_x(y)>-1, то xy монотонно возрастает; если E_x(y)<-1, то xy монотонно убывает. Аналогично,

E_x(y/x) = E_x(y)-E_x(x) = E_x(y)-1

Пример 3. Как связаны предельные и средние полные затраты предприятия, если эластичность полных затрат равна 1?

Решение. Пусть затраты выражены функцией y(x), где x - объем выпускаемой продукции. Тогда средние затраты равны y/x. Найдем эластичность отношения

E_x(y/x) = E_x(y)-E_x(x) = E_x(y)-1.

Но по условию E_x(y) = 1, поэтому E_x(y/x) = 0. Это означает, что с изменением объема продукции x средние затраты на единицу продукции не меняются, т.е. y/x = c, y = cx. Предельные издержки равны y' = c. Следовательно, предельные издержки совпадают со средними.

В анализе ценовой политики используется понятие эластичности спроса. Пусть d=d(p) функция спроса от цены товара p. Тогда эластичность определяется по формуле

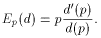
Для функции предложения s(p) аналогично вводится понятие эластичности

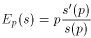
Отметим, что с увеличением цены объем спроса уменьшается. Поэтому функция спроса d(p) убывает, а функция предложения s(p) возрастает с ростом p. Следовательно, d'(p)<0, E_p(d)<0 и E_p(s)>0.

Отметим три вида спроса:

1. если E_p(d)<-1, то спрос считается эластичным;

2. если E_p(d)>-1, то спрос неэластичен;

3. если E_p(d) = -1, то спрос нейтрален.

Пример 4. Пусть известны функции спроса d=7-p и функция предложения s=p+1, где p - цена. Нужно найти равновесную цену и эластичности спроса и предложения.

Решение. Равновесная цена определяется из условия d=s, поэтому 7-p=p+1, откуда p=3. Найдем эластичность спроса и предложения

E_p(d) = p/(p-7), E_p(s) = p/(p+1).

Для равновесной цены p=3 получим E_p(d) = -0,75, E_p(s) = 0,75. Для значения p = 3 спрос является неэластичным, также как и функция предложения.

Дифференцируемость функции

Определение 1 (дифференцируемость в точке).Функция f(x) называется дифференцируемой в точке x, если приращение ∆ y этой функции в точке x представимо в виде

∆ y =A∆ x +ά(∆ x) ∆x,

(1)

где A - некоторое число, не зависящее от ∆ x, а lim_{∆ x→ 0} ά (∆x ) = 0.

В дальнейшем будем считать, что ά (0) = 0. В этом случае функция a(x) будет непрерывной в точке ∆ x = 0. Равенство 1 можно переписать иначе, так как функции ά (∆x), ∆x - бесконечно малые в точке ∆x = 0 и их произведение тоже бесконечно малая функция, поэтому

∆y =A∆ x +o(∆ x).

(2)

Справедлива теорема

Теорема 1.Для того чтобы функция была дифференцируема в точке x, необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Доказательство. Необходимость. Пусть функция дифференцируема, тогда ее приращение представимо в виде (1). Поделив (1) на ∆ x≠ 0 получим

∆ y/∆ x = A+ά(∆ x).

Переходя к пределу в последнем выражении при ∆ x→ 0, получим, что A=f'(x).

Достаточность. Пусть существует конечная производная f'(x), то есть существует конечный предел

lim_{∆ x→ 0} ∆ y/∆ x = f'(x).

Обозначим a(∆ x) = ∆ y/ ∆ x-f'(x). Отсюда вытекает представление (1).

Пример 1. Доказать, что функция |x| не дифференцируема в точке x = 0.

Решение. Найдем приращение функции в точке x = 0 :

∆ y = |∆ x|

Поэтому

lim_{∆ x→ -0} ∆ y/∆ x = -1, lim_{∆ x→+ 0} ∆ y/∆ x = 1,

следовательно, функция |x| в точке x = 0 не дифференцируема.

Следующая теорема выражает связь между непрерывностью и дифференцируемостью.

Теорема 2 (дифференцируемость и непрерывность).Если
функция дифференцируема в точке x, то она непрерывна в этой точке.

Доказательство. Так как функция дифференцируема в точке x, то то ее приращение представимо в виде (1), из которого следует, что lim_{∆ x→ 0} ∆ y = 0, что означает непрерывность функции в данной точке.

Заметим, что из непрерывности в данной точке не следует дифференцируемость в этой точке. Это видно из рассмотренного выше примера1.

Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на некотором множестве X, то функция называется гладкой на этом множестве. Если производная допускает конечное число точек разрыва (причем первого рода), то такая функция называется кусочно гладкой.

Правила дифференцирования

Приведем основные правила для нахождения производной:

1. Производная постоянной равна нулю, то есть c' = 0.

2. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, то есть

(u(x)± v(x))' = u'(x)± v'(x).

3. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, то есть

(u(x)v(x))' = u'(x)v(x)+u(x)v'(x).

Следствие 1.Постоянный множитель можно выносить за знак производной:

(cu(x))' = cu'(x).

4. Производная частного двух дифференцируемых функций может быть найдена по формуле

(u(x)/v(x))' = (u'(x)v(x)-u(x)v'(x))/v²(x)

при условии, что v(x)≠ 0.

5. Производная сложной функции:

h(x)=g(f(x))- сложная функция

h´(x)=g´(f(x))· f´(x)

Формулы дифференцирования

1. (u^a(x))' = a u^a-1(x)u'(x), в частности,

(1/u(x))' = -u'(x)/u²(x), (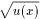)' = u'(x)/2;

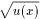2. (log_au(x))' = (u'(x)log_ae)/u(x) при 0<a≠1, u(x)>0, вчастности, (ln u(x))' = u'(x)/u(x);

3. (a^u(x))' = a^u(x)ln a u'(x) при 0<a≠1, в частности, (e^u(x))' = u'(x)e^u(x);

4. (sin u(x))' = cos u(x)u'(x);

5. (cos u(x))' = -sin u(x)u'(x);

6. (tgu(x))' = u'(x)/cos²u(x) x≠ p/2+p n, n=0,+-1,...;

7. (ctgu(x))' = -u'(x)/sin²u(x) x≠ p n, n=0,+-1,...;

8. (arcsin u(x))' = u'(x)/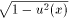, -1<u(x)<1;

9. (arccos u(x))' = -u'(x)/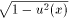, -1<u(x)<1;

10. (arctg u(x))' = u'(x)/(1+u²(x));

11. (arcctgu(x))' = -u'(x)/(1+u²(x)).

Введем гиперболические функции:

sh x = (1/2)(e^x-e^-x)- гиперболический синус;

ch x = (1/2)(e^x+e^x)- гиперболический косинус;

th x = sh x/ch x -гиперболический тангенс;

cth x = ch x/sh x - гиперболический котангенс.

Из определения гиперболических функций элементарно вытекают следующие формулы для нахождения их производных.

1. (sh x)' = ch x;

2. (ch x)' = sh x;

3. (th x)' = 1/ch² x;

4. (cth x)' = -1/sh² x.

Пример1. Найти y', если

1. y(x) = x³arcsin x.

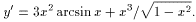
2. y(x) = ln sin (x²+1).

y' = (2xcos(x²+1))/sin(x²+1) = 2x ctg(x²+1)

Замечание. Производная любой элементарной функции является элементарной функцией, то есть операция дифференцирования не выводит из класса элементарных функций.

Производные высших порядков

Предположим, что функция f'(x) является дифференцируемой в некоторой точке x интервала (a,b), то есть имеет в этой точке производную. Тогда данную производную называют второй производной и обозначают f⁽²⁾(x), f''(x) или y⁽²⁾, y''(x). Аналогично можно ввести понятие второй , третьей и т. д. производных. По индукции можно ввести понятие n-ой производной:

y(n) = (y(n-1))'.

(3)

Функцию, имеющую на некотором множестве конечную производную порядка n, называют n раз дифференцируемой на этом множестве. Методика нахождения производных высших порядков предполагает умение находить производные первого порядка, о чем говорит формула (3).

Если u(x), v(x) две дифференцируемые функции, то для нахождения производной их произведения справедлива формула Лейбница

(u(x)v(x))⁽ⁿ⁾ = u⁽ⁿ⁾v+nu^(n-1)v'+(n(n-1)/2)u^(n-2)v''+...+ uv⁽ⁿ⁾ =

= S_{k = 0}ⁿC_n^ku^(n-k)v^(k),

где

C_n^k = (n(n-1)(n-2)...(n-k+1))/k!, u⁽⁰⁾ = u, v⁽⁰⁾ = v.

Данная формула Лейбница особенно эффективна в случае, когда одна из перемножаемых функций имеет конечное число отличных от нуля производных и легко вычислить производные другой функции.

Пример 9. Пусть y = e^x(x²-1). Найти y⁽¹⁰⁾. Положим u(x) = e^x,
v(x) = (x²-1). Согласно формуле Лейбница

y⁽¹⁰⁾ = (e^x)⁽²⁵⁾(x²-1)+10(e^x)⁽⁹⁾(x²-1)'+(10· 9/2) (e^x)⁽⁸⁾(x²-1)'',

так как следующие слагаемые равны нулю. Поэтому

y⁽¹⁰⁾ = e^x(x²-1)+10e^x2x+(10· 9/2)e^x(2) = e^x(x²+20x+89)

Правило Лопиталя

Будем говорить, что отношение функций f(x)/g(x) представляет собой неопределенность вида 0/0 при x→ a, если

lim_{x→ a}f(x) = lim_{x→ a}g(x) = 0.

Раскрыть неопределенность - это значит вычислить предел
lim_{x→ a}f(x)/g(x), если он существует. Аналогично можно ввести понятие неопределенности при x→ a-0 (x→a+0), x→±∞.

Следующая теорема дает правило раскрытия неопределенности вида 0/0.

Теорема 1 (правило Лопиталя).Пусть множество 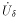(a) - проколотая δ - окрестность точки a, функции f(x),g(x) определены и дифференцируемы на 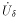, g'(x)≠ 0,

lim_{x→ a}f(x) = lim_{x→ a}g(x) = 0.

Тогда если существует lim_{x→ a}f'(x)/g'(x), то существует и предел lim_{x→ a}f(x)/g(x), причем справедливо соотношение

lim_{x→ a}f(x)/g(x) = lim_{x→ a}f'(x)/g'(x).

Данная теорема без изменений переносится на случай неопределенности вида ∞/∞

Замечание. Сформулированная теорема представляет собой лишь достаточное условие. То есть предел отношения функций может существовать и в случае, когда предел отношения производных не существует.

Например, пусть f(x) = x+sin x, g(x) = x-sin x, x_→ ∞. Попробуем применить правило Лопиталя

lim_x→∞(x+sinx)/(x-sinx) = ∞/∞= =lim_x→ ∞ (x+sinx)'/(x-sinx)' = lim_x→ ∞ (1+cosx)/(1-cosx),

но предел последнего выражения не существует, однако, если поделить числитель и знаменатель на x, то легко получим конечное значения предела:

lim_x→ ∞ (x+sin x)/(x-sin x) = lim_x→∞ (1+sin x/x)/(1-sin x/x) = 1

Замечание. Если производные f'(x),g'(x) удовлетворяют тем же требованиям, что и сами функции, то правило Лопиталя можно применить повторно, т.е. предел отношения первых производных можно заменить пределом отношения вторых производных и т.д.

Кроме рассмотренных выше видов неопределенностей вида 0/0 и ∞/∞ часто встречаются неопределенности видов: 0· ∞, ∞-∞, 1^∞, 0^∞, ∞⁰. Все эти неопределенности сводятся к двум вида 0/0 и ∞/∞ путем алгебраических преобразований. Продемонстрируем это на примере неопределенностей вида 1∞, 0∞, ∞⁰. Каждая из этих неопределенностей имеет вид

y = f(x)g(x),

(4)

где lim_{x→ a}f(x) = 1;0; ∞, lim_{x→ a}g(x) = ∞;0, Прологарифмировав выражение (4), получим (при f(x)>0 )

ln y = g(x)ln f(x).

Последнее выражение представляет собой при x_→ a неопределенность вида 0· ∞. Покажем, как свести неопределенность вида 0· ∞ к неопределенности вида 0/0 или ∞/∞

Пусть y = f(x)g(x), где lim_{x→ a}f(x) = 0, а lim_{x→ a}g(x) = Ґ. Но y можно записать иначе, а именно y = f(x)/(1/g(x)), а данное выражение представляет собой при x_→ a неопределенность вида 0/0.

Проиллюстрируем на примерах применение правила Лопиталя.

Пример 1. Применяя правило Лопиталя, вычислить пределы:

1. lim_x→0(e^ax-e^-2ax)/ln (1+x) = 0/0= lim_{x→ 0}(ae^ax+2ae^-2ax)/(1/(1+x)) = 3a.

2. lim_x→∞(e^1/x2-1)/(2arctg x²-p) = 0/0= lim_x→ ∞(-2x^-3e^1/x2)/(4x/(1+x⁴)) = lim_x→ ∞-e^1/x2(1+x⁴)/2x⁴ = -1/2.

3. lim_{x→ 1}(1/ln x-1/(x-1)) = ∞-∞ = lim_{x→ 1} (x-1-ln x)/((x-1)ln x) = lim_{x→ 1}(1-1/x)/(ln x+1-1/x) = lim_{x→ 1}(x-1)/(xln x+x-1) = lim_{x→ 1}1/(ln x+2) = 1/2.

4. lim_{x→ +0}(1/x)^{sin x}. Пусть y = (1/x)^{sin x}, тогда ln y = sin xln (1/x),

lim_x→+0lny = limlim_{x→ +0}sinxln (1/x). lim_{x→ +0}lny = lim_{x→ +0}(-lnx)/(1/sinx) = lim_{x→ +0}(-1/x)/(-cosx/sin²x) = lim_{x→ +0}sin²x/(xcosx) = 0.

Следовательно, lim_{x→ 0} y = e⁰ = 1.

Понятие дифференциала. Геометрический смысл дифференциала. Инвариантность формы первого дифференциала.

Рассмотрим функцию y = f(x), дифференцируемую в данной точке x. Приращение ∆y ее представимо в виде

∆y = f'(x)∆x +ά(∆x) ∆x,

где первое слагаемое линейно относительно ∆x, а второе является в точке ∆x = 0 бесконечно малой функцией более высокого порядка, чем ∆x. Если f'(x)≠ 0, то первое слагаемое представляет собой главную часть приращения ∆y. Эта главная часть приращения является линейной функцией аргумента ∆x и называется дифференциалом функции y = f(x). Если f'(x) = 0, то дифференциал функции по определению считается равным нулю.

Определение 1 (дифференциал).Дифференциалом функции y = f(x) называется главная линейная относительно ∆x часть приращения ∆y, равная произведению производной на приращение независимой переменной

dy = f'(x)∆x.

Заметим, что дифференциал независимой переменной равен приращению этой переменной dx = ∆ x. Поэтому формулу для дифференциала принято записывать в следующем виде:

dy = f'(x)dx.

(5)

Геометрический смысл

Возьмем на графике функции y = f(x) произвольную точку M(x,y) (рис21.). Проведем касательную к кривой y = f(x) в точке M, которая образует угол f с положительным направлением оси OX, то есть f'(x) = tg f. Из прямоугольного треугольника MKN

KN = MNtgf = ∆ xtg f = f'(x) ∆ x,

то есть dy = KN.

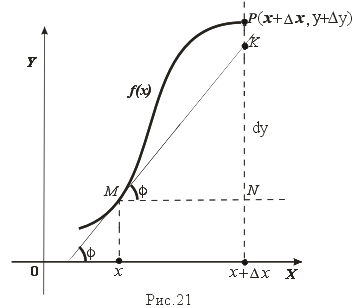
Таким образом, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y = f(x) в данной точке, когда x получает приращение ∆ x.

Свойства дифференциала

1. d c = 0;

2. d(cu(x)) = c d u(x);

3. d(u(x) ±v(x)) = d u(x) ± d v(x);

4. d(u(x) v(x)) = v(x) d u(x) + u(x)d v(x);

5. d(u(x) / v(x)) = (v(x) d u(x) - u(x) d v(x)) / v²(x).

Укажем еще на одно свойство, которым обладает дифференциал, но не обладает производная. Рассмотрим функцию y = f(u), где u = φ(x), то есть рассмотрим сложную функцию y = f(φ(x)). Если каждая из функций f и φ являются дифференцируемыми, то производная сложной функции согласно теореме, равна y' = f'(u)· u'. Тогда дифференциал функции

dy = f'(x)dx = f'(u)u'dx = f'(u)du,

так как u'dx = du. То есть

dy = f'(u)du.

(6)

Последнее равенство означает, что формула дифференциала не изменяется, если вместо функции от x рассматривать функцию от переменной u. Это свойство дифференциала получило название инвариантности формы первого дифференциала.

Замечание. Отметим, что в формуле (5) dx = ∆ x, а в формуле (6) du является лишь линейной частью приращения функции u.

Рассмотрим выражение для первого дифференциала

dy = f'(x)dx.

Пусть функция, стоящая в правой части, является дифференцируемой функцией в данной точке x. Для этого достаточно, чтобы y = f(x), была дифференцируема два раза в данной точке x, а аргумент либо является независимой переменной, либо представляет собой дважды дифференцируемую функцию.