Кинематический анализ стержневых расчетных схем

Если расчет конструкции производится аналитически, то для выбора методики расчета должен быть выполнен кинематический анализ расчетной схемы [1]. Он должен показать, является ли система геометрически изменяемой, ста­тически определимой или статически неопределимой. В первом случае система не может нести нагрузку и не подлежит расчету методами строительной механики, во втором случае все внутренние усилия находятся из условий статики, а в третьем — используются специальные методы расчета статически неопределимых систем (п. 4.1). Кинематиче­ский анализ включает аналитическое определение числа степеней свободы (или степени статической неопределимости) системы и анализ ее структуры. Числом степеней свободы системы называют число взаимно независимых координат, однозначно определяющих ее положение в пространстве, при условии, что все элементы системы считаются абсолютно жесткими.

Расчетная схема в кинематическом анализе рассматривается как система, состоящая из нескольких абсолютно жестких блоков (стержней), соединенных идеальными связями с основанием и друг с другом. Связи разделяются по количеству степеней свободы, которые они отнимают у присоединяемого ими блока. Кроме того, они могут быть жесткие и упругие, двухсторонние и односторонние.

Жесткие связи моделируются опорными стержнями или жесткими заделками. Опорные стержни — это условные (т. е. существующие только на расчетной схеме, но моделирующие действительное взаимодействие тел) абсолютно жесткие, весьма длинные по сравнению с возможными переме­щениями стержни, соединенные с блоками идеальными шарнирами. Каждый опорный стержень отнимает у блока одну степень свободы, т. е. запрещает линейное перемещение точки, с которой он связан, вдоль оси опорного стержня. Виды связей блоков и соответствие связей и опор балок, используемых в курсе «Сопротивление материалов», показаны на рис. 2.3.

Упругие связи не отнимают степеней свободы, но создают реакции, пропорциональные перемещениям точки присоединения этой связи в направлении этой связи. С помощью упругих связей моделируют, например, податливое основание. В кинематическом анализе эти связи рассматривают как жесткие. Однако если они приводят к возникновению значительных перемещений, то расчет следует вести по деформированной (т. е. не линейной) схеме.

Связи, которые ограничивают перемещения в обоих направлениях и воспринимают нагрузки любого знака, называют двухсторонними связями. Если связь может воспринимать нагрузки только одного знака, то ее называют односторонней связью. Такой связью является колесо, опертое на рельс, поскольку контакт может передавать усилие только в одном направлении. Канатная оттяжка может воспринимать только растягивающие усилия, но при сжатии теряет свою форму. Такие связи могут явиться причиной нелинейности системы, если действующие нагрузки знакопеременны.

Для плоских систем кинематический анализ производится по следующим правилам. Блок на плоскости имеет три степени свободы. Таким образом, чтобы закрепить блок, требуется как минимум три опорных стержня, оси которых не пересекаются в одной точке (рис. 2.3, а). Плоский шарнир, соединяющий два блока (простой шарнир), отнимает у системы две степени свободы (рис. 2.3, б).Жесткая заделка блока в основании или в соседнем блоке моделируется тремя стержнями и отнимает три степени свободы (рис.

1.3, в, г). На основании сказанного число степеней свобо­ды системы вычисляют по формуле

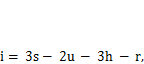(2.2)

где s, и, h, r — соответственно количество блоков, простых шарниров, жестких связей (с основанием или между блоками) и опорных стержней.

По результатам расчета параметра i(2.2) могут быть сделаны следующие предварительные выводы. Если i> 0, то система геометрически изменяема, если же i< 0, то систе-

ма | | раз статически неопределима. Для геометрически не­изменяемой и статически определимой системы получится = 0.

Так, система на рис. 2.4, а имеет одну степень свободы 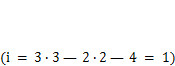. Система на рис. 2.4, б имеет четыре жесткие связи, две между стержнями и две с основанием. Она статически неопределима 3 раза 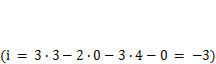. Такая конструкция называется внешне статически неопре­делимой. Для стержневой системы (рис. 2.4, в) , она геометрически неизменяема и статически определима.

Плоский замкнутый контур без шарниров трижды статически неопределим. Если представить конструкцию на рис. 2.4, г как систему из четырех жестко соединенных стержней, то получим . Если же в контур ввести один плоский шарнир (рис. 2.4, д), то получим . Таким образом, введение шарнира вместо жесткой связи снимает одну степень не­определимости. Статическая неопределимость, обусловлен­ная наличием замкнутых контуров, называется внутренней.

Замкнутый контур с тремя шарнирами внутренне статически определим, если шарниры не лежат на одной прямой. Ферменная структура на рис. 2.4, е состоит из семи стержней, соединенных девятью простыми шарнирами (отмечены дугами). Для нее .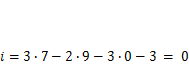

Однако аналитическое условие является необходимым, но не достаточным. Поэтому требуется анализ структуры системы. Рассмотрим, например, стержневую систему на рис. 2.5, а, для которой 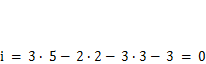. Однако не сложно увидеть, что она состоит из статически неопреде­лимого портала и геометрически изменяемой двухстержневой системы. Кроме того, конструкция будет геометрически изменяемой (подвижной), если оси всех опорных стержней пересекаются в одной точке или параллельны (рис. 2.5, б, в). Мгновенно геометрически изменяемой является и система, в которой три шарнира лежат на одной прямой (рис. 2.5, г).

Аналогичные правила можно записать для пространствен­ной системы. Блок в пространстве имеет шесть степеней свободы. Каждый опорный стержень отнимает у блока одну степень свободы. Жесткая заделка блока в основании или жесткое соединение двух блоков моделируется шестью стержнями и отнимает у системы шесть степеней свободы. Соединение двух блоков простым сферическим шарниром (3D) отнимает у системы три степени свободы. На основа­нии сказанного число степеней свободы пространственной системы вычисляют по формуле

где и — количество простых сферических шарниров; h— количество жестких связей с основанием и между блоками; r — число опорных стержней.

Жесткий замкнутый контур шесть раз внутренне статически неопределим. Для пространственной стержневой системы (рис. 2.4, ж), в которой шесть стержней соединены

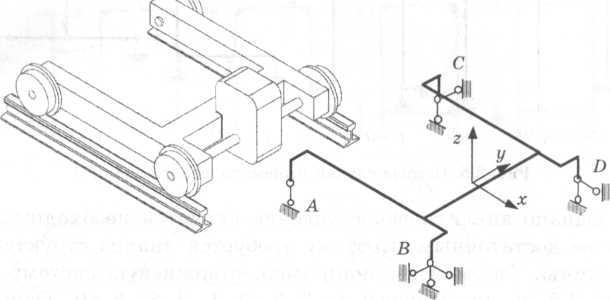Рис. 2.6. Пример моделирования условий опирания подвижной конструкции на рельс

восьмью простыми пространственными шарнирами, запишем

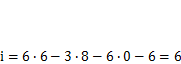
Эти шесть степеней свободы отражают возможность по­воротов стержней относительно собственных осей. Пример моделирования взаимодействия подвижной платформы с рельсом показан на рис. 2.6. Вертикальные связи моделируют опирание колес на рельс. Опорные стержни по оси у отражают контакт реборд с головкой рельса (показан случай контакта колес В и С). Опорные стержни по оси х характеризуют взаимодействие приводных колесВ и Dс рельсом через силы трения. Вертикальные стержни над опорами соответствуют радиусу колеса.