Построение цикла и определение величины перераспределения груза

Цикломв таблице перевозок называется ломаная линия с вершинами в клетках и ребрами, расположенными вдоль строк или столбцов, удовлетворяющая двум требованиям:

а) ломаная должна быть связной, т.е. из любой ее вершины можно попасть в другую вершину, двигаясь по ребрам;

б) в каждой вершине цикла сходятся ровно два ребра - одно по строке, другое по столбцу.

Замечание: в цикле возможны самопересечения, но они происходят только не в вершинах цикла. Примеры построения циклов показаны ниже.

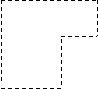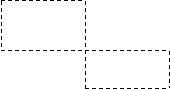Теорема 3. Если в таблице перевозок m строк и n столбцов, и перевозками заполнено (m+n-1) клеток, то существует цикл, одна из вершин которого расположена в свободной клетке, а все остальные вершины в занятых клетках. Такой цикл называется циклом пересчета свободной клетки.

Теорема 4. В таблице перевозок для каждой свободной клетки существует единственный цикл пересчета.

Метод потенциалов позволяет не только оценить оптимальность плана, но и улучшить его с помощью цикла пересчета свободной клетки.

Алгоритм метода потенциалов

1. Поставим в соответствие каждой станции 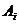переменную 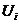, а каждой станции 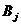– переменную .

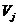2. Для каждой заполненной клетки ( 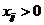) составим уравнение 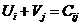. Придадим значение 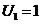(можно любое другое) и находим все остальные потенциалы.

3. Проверим оптимальность опорного решения. Для этого вычисляем сумму потенциалов для свободных клеток. Если найденная сумма (обозначим ее 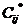) меньше стоимости перевозок, то есть 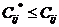для всех свободных клеток, то опорное решение является оптимальным. Запишем решение задачи: план перевозок, минимальное значение функции цели. Если это условие не выполняется хотя бы в одной клетке, то опорное решение не оптимально и надо перейти к следующему опорному плану. Найдем разность (невязку) 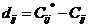для всех свободных клеток и будем записывать ее в таблице в нижний правый угол клетки, если 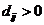. Затем выбираем ту клетку, где невязка максимальна (если два нарушения одинаковы, то выбираем любую из клеток).

4. В выбранную клетку нужно поставить перевозку. Для этого строим цикл пересчета свободной клетки: этот цикл должен иметь одну вершину в отмеченной свободной клетке, а все остальные – в занятых.

5. Пронумеруем вершины цикла, начиная с пересчитываемой свободной клетки. Определим величину сдвига по циклу θ, как минимальную из перевозок стоящих в четных вершинах цикла.

6. Вычтем величину θ из перевозок в четных вершинах цикла и прибавим ее к перевозкам в нечетных вершинах. Получен новый опорный план. После этого переходим к пункту 3.

Пример

Продолжим решение задачи, на примере которой рассмотрены методы нахождения первого опорного плана. Напомним, что за опорное решение мы решили принять решение, полученное при расчете методом двойного предпочтения.

С помощью метода потенциалов найдем оптимальное решение. Придадим потенциалу U₂ значение 0, а остальные потенциалы для занятых клеток определим из системы уравнений (6.5):

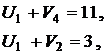
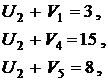
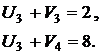
Из этой системы, подставляя в нее значение 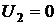, найдем остальные потенциалы и запишем их в таблицу. Например, 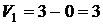, 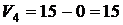и т.д.

Получим таблицу:

Потенциалы	V1 = 3	V2 = 7	V3 = 9	V4 = 15	V5 = 8	Запасы
U1 = -4		3 21 –		19 +
U2 = 0		+		2 –
U3 = -7
Потребности

Проверим выполнение условия оптимальности плана (1.6):

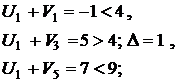
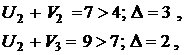
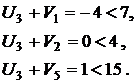
План не является оптимальным, так как имеются нарушения условий (6.6) в клетках A₁-B₃, A₂-B₂ и A₂-B₃. Наибольшая невязка (нарушение) равна ∆ = 3, следовательно, пересчет начинаем с клетки A₂-B₂. Этой клетке присваивается номер 1 и строится цикл пересчета по правилам изложенным выше. Все клетки в которых лежат вершины цикла последовательно нумеруются, четным вершинам приписывается знак –, а нечетным +. Величина сдвига по циклу находится как минимальное значение из всех перевозок в четных вершинах цикла и равна 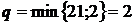. Она вычитается из перевозок в четных вершинах цикла и прибавляется к перевозкам в нечетных. Получаем новый план, для которого вновь находим потенциалы и проверяем условия (6.6):

	V1 = 3	V2 = 4	V3 = 6	V4 = 12	V5 = 8	Запасы
U1 = -1			+	21 -
U2 = 0
U3 = -4			7 -	3 +
Потребности

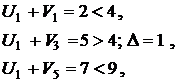
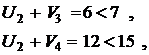
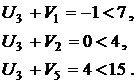
План не является оптимальным, так как условие (6.6) не выполняется в клетке A₁-B₃ с невязкой ∆=1, следовательно, пересчет начинаем с клетки A₁-B₃. Величина сдвига по циклу 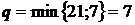вычитается из перевозок в четных вершинах цикла и прибавляется к перевозкам в нечетных. Получаем новый план, для которого вновь находим потенциалы и проверяем условия оптимальности. Из приведенного примера видно, что фактически цикл пересчета освобождает «невыгодные» клетки с большой стоимостью или, по крайней мере, уменьшает величину перевозки в таких клетках.

	V1 = 3	V2 = 4	V3 = 5	V4 = 12	V5 = 8	Запасы
U1 = -1
U2 = 0
U3 = -4
Потребности

Опорный план оптимален, так как все невязки равны нулю:

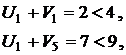
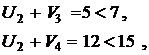
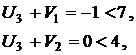
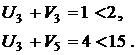
Вычисляем функцию цели:

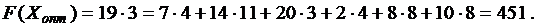
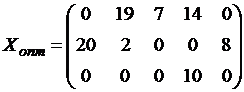Ответ: , 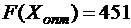.