Основные положения симплекс-метода

Пусть задана задача линейного программирования в виде канонической модели.

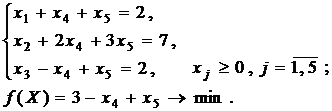(4.1)

Рассмотрим идею симплекс-метода на этом примере. Нетрудно убедиться, что система (4.1) совместна. Ее ранг r = 3, значит базисных переменных 3, а свободных переменных k = 5 – 3 = 2. Полагая свободные переменные x₄, x₅ равными нулю, получим первое опорное решение:

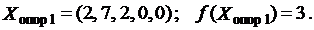
В начальном плане свободными, а значит равными нулю являются переменные х₄, х₅. Посмотрим, нельзя ли за счет увеличения х₄ и х₅ уменьшить значение целевой функции. У нас f(X) =3- х₄+ х₅ , неизвестная х₅ входит в выражение целевой функции со знаком плюс, поэтому ее увеличение приводит к увеличению функции. И это нам невыгодно. В то же время неизвестная х₄ входит в выражениях со знаком минус. Поэтому ее увеличение сопровождается уменьшением значения функции f(Х). Увеличение свободной неизвестной х₄ вызывает соответствующие изменения базисных переменных х₁, х₂, х₃. Эти изменения могут оказаться такими, что базисные переменные станут отрицательными. Мы должны позаботиться о том, чтобы этого не произошло.

Оставим у переменной х₅ - значение равное нулю и рассмотрим уравнения, которые в этом случае получаются из системы (4.1):

x₁ + x₄=2,

x₂ + 2x₄=7,

x₃ – x₄=2.

Так как х₁= 2 – х₄ и 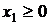, то х₄ < 2; аналогично х₂=7 – 2х₄и 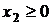, следовательно . Так как х₃ = 2 + х₄, то здесь х₄ может возрастать неограниченно. Далее выберем максимально возможное значение х₄ равное 2; при этом х₁ = 0, х₂ = 3, х₃ = 4, х₄ = 2, х₅ = 0.

Мы перешли к новому опорному решению: X_опор2 = (0, 3, 4, 2, 0). Сравнивая X_опор1и X_опор2, видим, что х₁ стала свободной, а х₄ - базисной. Модель надо преобразовать так, чтобы х₄ присутствовало только в первом уравнении системы (4.1), функция f(X) должна быть выражена через свободные переменные х₁ и х₅. Из первого уравнения х₄ = 2 – х₁ – х₅, и задача ЛП будет такой:

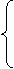x₂ – 2x₁ + x₅ = 3,

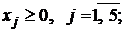x₃ + x₁ + 2x₅ = 4, (4.2)

x₄ + x₁ + x₅ = 2;

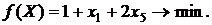
Теперь видно, что f(X) не может быть уменьшена за счет увеличения х₁ и х₅. Значит, мы получили оптимальное решение. Запишем его.

Х_min = (0, 3, 4, 2, 0); f_min= f(Х_min) = 1.

Идею, рассмотренную в примере, используем для того, чтобы сформулировать правило преобразования симплекс-таблиц для решения задач симплексным методом.

4.2. Правило преобразования симплекс-таблиц

Мы в пункте (4.1) увидели, что переход от одного опорного решения к другому начинается с исследования коэффициентов целевой функции и затем вычисляются коэффициенты новой модели задачи ЛП. Запишем требования к исходной модели задачи.

1. Задача линейного программирования должна быть представлена в виде канонической модели.

2. Целевая функция должна минимизироваться.

3. При занесении в таблицу у целевой функции меняются на противоположные знаки коэффициентов при свободных переменных.

Запишем полученную каноническую задачу:

а₁₁х₁ + a₁₂x₂ + х₃= b₁,

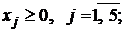а₂₁х₁ + a₂₂x₂ + х₄= b₂,

а₃₁х₁ +a₃₂x₂ + х₅= b₃,

f(X) = с₀ – (с₁х₁ +с₂х₂)→min.

В задаче Х_опор1 = (0,0, b₁, b₂, b₃), f₁= f (Х) = с₀. Внесем коэффициенты этой модели в симплекс-таблицу (см. табл. 4.1).

Таблица 4.1

Базис	В	х1	х2	х3	х4	х5
х3	b1	а11	al2
х4	b2	а21	a22
х5	b3	а31	a32
f(х)	с0	с1	с2

4. Рассмотрим последнюю строку таблицы 4.1 (коэффициенты целевой функции). Нас интересуют знаки с₁ и с₂.

а) если хотя бы один из коэффициентов положителен, например с₁ > 0, то отмечаем стрелкой столбец таблицы, где находится с₁. Этот столбец назовем ключевым. Если положительны оба коэффициента, то выберем наибольший из них;

б) если с₁≤ 0 и с₂ ≤ 0, то таблицу не надо преобразовывать. Из таблицы находится оптимальное решение.

5. Выберем ту базисную переменную, которая будет свободной вместо х₁, для этого выберем положительные из коэффициентов а_i1, i = 1, 2, 3.

Пусть для определенности у нас а₁₁ > 0, а₂₁ > 0, a_3l ≤ 0. Если все а_i1 отрицательны или равны нулю, то задача решений не имеет, т.к. целевая функция не ограничена. Пусть, кроме того, .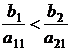

6. У нас a₁₁ >0, a₂₁ >0, тогда выберем 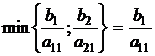. Это означает, что х₁ будет базисной переменной, а х₃ - свободной. Переходим к следующей таблице:

Таблица 4.2

Базис	В	х1	х2	х3	х4	х5
х1	β1		al2*	al3*
х4	β2		a22*	a23*
х5	β3		a32*	a33*
f(х)	d0		d2	d3

7. Сначала заполняем первую строку таблицы 4.2, эта строка соответствует базисной переменной х₃ в таблице 4.1. Все коэффициенты 1-ой строки таблицы 4.1. делим на разрешающий элемент а₁₁, результат запишем в первую строку таблицы 4.2. Эта строка называется разрешающей.

, , .

С помощью разрешающей строки, делая простые вычисления, мы должны получить в остальных строках ключевого столбца нули.

8. Умножим разрешающую строку последовательно на (-а₂₁), (-а₃₁), (–с₁). Полученные строки чисел прибавим ко второй, потом к третьей, затем к последней строке таблицы 4.1, а результаты вычислений поставим во вторую, третью и последнюю строку таблицы 4.2, где:

; ; ;

; ; ;

; ; .

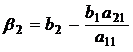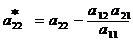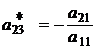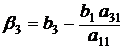9. Мы получили новую таблицу, а следовательно, новый опорный план: Х_опор2 = (β₁, 0, 0, β₂, β₃), f₁= f (Х_опор2) = d₀.

10. Если d₁ ≤0, d₂ ≤0, то решение оптимально. Если среди них есть положительные, то процесс преобразования таблиц надо продолжать.

Пример.Решим симплекс-методом пример из п.2. Модель задачи ЛП в этом примере стандартная:

12х₁ + 4х₂ ≤300,

4х₁ + 4х₂ ≤120,

3х₁ + 12х₂ ≤252, х₁ ≥0, х₂ 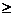0;

f(х) = 30х₁ +40х₂ ® mах.

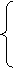1) Перейдем к канонической модели. Для этого подберем х₃, х₄, х₅, уравнивающие левые и правые части системы ограничений. Затем перейдем к задаче минимизации: f(x) ® max, тогда f₁(х) = – f(х) ® min. Запишем каноническую модель:

12х₁ +4х₂ + х₃ =300,

4х₁ +4х₂+х₄ =120,

3х₁ +12х₂+х₅ =252, х_j ≥0, j = 1,…5;

f₁(х) = – (30х₁ +40х₂) ® min.

2) Внесем коэффициенты в таблицу:

Таблица 4.3

Базис	В	х1	х2	х3	х4	х5
х3
х4
х5
f1(х)

В таблице 4.3 с₁ = 30; с₂ = 40; 40 = max{30;40}, неизвестная х₂ – перейдет в базисную. Столбец ее коэффициентов будет ключевым. Все элементы ключевого столбца положительны.

2) Найдем разрешающую строку и разрешающий элемент в таблице:

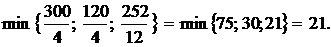
Третья строка в таблице является разрешающей. Эта строка базисной переменной х₅, поэтому х₅ будет свободной переменной. Элемент, находящийся в таблице 4.3 на пересечении выделенных строки и столбца будет разрешающим элементом, равным 12. Замена базисной переменной х₅ на свободную х₂ в таблице 4.3 показаны стрелками.

3) Разделим все элементы третьей (разрешающей) строки таблицы 4.3 на 12. Далее все полученные элементы строки умножим последовательно на (– 4), (– 4), (– 40) и сложим с первой, второй и последней строкой таблицы 4.3. Составим новую симплекс-таблицу:

Таблица 4.4.

Базис	В	х1	х2	х3	х4	х5
х3						-1/3
х4						-1/3
x2		1/4				1/12
f1(х)	-840					-10/3

4) Снова изучим последнюю строку таблицы 4.4. Там есть положительный коэффициент 20. Отметим ключевой столбец, выберем в нем элемент а₂₁. Тогда:

.

Будем работать с таблицей 4.4. так же, как и с таблицей 4.3. Делим вторую строку на 3. Затем получаем в столбце для переменной х₁ нули в остальных строках, умножая элементы разрешающей строки последовательно на (-11), , (–20). Результаты поместим в таблицу 4.5:

Таблица 4.5.

Базис	В	х1	х2	х3	х4	х5
х3					-11/3	8/9
х1					4/3	-1/9
х2					-1/12	1/9
f1(х)	-1080				-20/3	-10/9

В последней строке таблицы 4.5 нет положительных чисел, решение оптимально.

Ответ: Х_min = (12, 18, 84, 0, 0); f₁ (Х_min) = -1080.

Ответ исходной задачи: Х_mах = (12, 18, 84, 0, 0); f (Х_mах) = 1080.