Решение контрольных задач по теме «Теория графов».

Задание 1. Компоненты сильной связности ориентированного графа.

С помощью матрицы смежности найти компоненты сильной связности ориентированного графа D.

Cоставляем матрицу смежности A(D) размерности 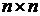(n− количество вершин) для данного ориентированного графа: она состоит из нулей и единиц, номера строк – индексы вершин , из которых исходят дуги, номера столбцов – индексы вершин, в которые дуги входят (если есть дуга, исходящая из вершины v_i и входящая в v_j, то элемент матрицы смежности, стоящий на пересечении i-той строки и j-того столбца равен 1, иначе – 0.).

Для того, чтобы выделить компоненты сильной связности, необходимо сначала найти матрицу достижимости T(D) ориентированного графа по первой формуле утверждения 3, затем находим матрицу сильной связности S(D) ориентированного графа (она должна быть симметрической) по второй формуле из того же утверждения.

Алгоритм выделения компонент сильной связности

1. Присваиваем p=1 (p − количество компонент связности), .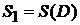

2. Включаем в множество вершин V_p компоненты сильной связности D_p вершины, соответствующие единицам первой строки матрицы S_p. В качестве матрицы A(D_p) возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V_p.

3. Вычеркиваем из S_p строки и столбцы, соответствующие вершинам из V_p. Если не остается ни одной строки (и столбца), то p- количество компонент сильной связности. В противном случае обозначим оставшуюся после вычеркивания срок и столбцов матрицу как S_p+1, присваиваем p=p+1 и переходим к п. 2.

Пример

Выделим компоненты связности ориентированного графа, изображенного на рис. 6. В данной задаче количество вершин n=5.

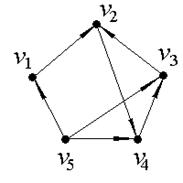
Рис. 6.

Значит, для данного ориентированного графа матрица смежности будет иметь размерность 5×5 и будет выглядеть следующим образом

.

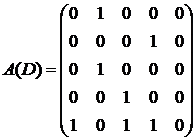Найдем матрицу достижимости для данного ориентированного графа по формуле 1) из утверждения 3:

, ,

,

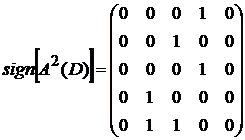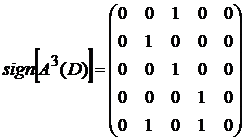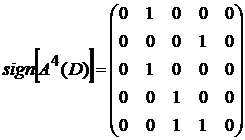Следовательно,

.

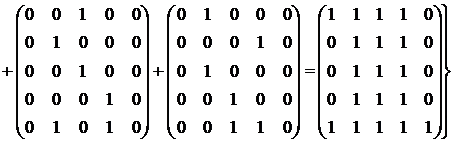Таким образом, матрица сильной связности, полученная по формуле 2) утверждения 3, будет следующей:

.

Присваиваем p=1 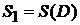и составляем множество вершин первой компоненты сильной связности D₁: это те вершины, которым соответствуют единицы в первой строке матрицы S(D). Таким образом, первая компонента сильной связности состоит из одной вершины .

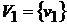Вычеркиваем из матрицы S₁(D) строку и столбец, соответствующие вершине v₁, чтобы получить матрицу S₂(D):

.

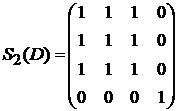Присваиваем p=2. Множество вершин второй компоненты связности составят те вершины, которым соответствуют единицы в первой строке матрицы S₂(D), то есть 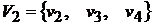. Составляем матрицу смежности для компоненты сильной связности 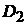исходного графа D − в ее качестве возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V₂:

.

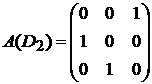Вычеркиваем из матрицы S₂(D) строки и столбцы, соответствующие вершинам из V₂ ,чтобы получить матрицу S₃(D), которая состоит из одного элемента:

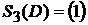
и присваиваем p=3. Таким образом, третья компонента сильной связности исходного графа, как и первая, состоит из одной вершины .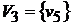

Таким образом, выделены 3 компоненты сильной связности ориентированного графа D:

D1:

D2: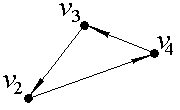

D3:

Задание 2. Расстояния в ориентированном графе

С помощью алгоритма фронта волны найти расстояния в ориентированном графе D: диаметр, радиус и центры.

Пусть 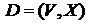ориентированный граф с n³2 вершинами и v,w (v¹w) – заданные вершины из V.

Алгоритм поиска минимального пути из 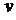в в 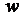ориентированном графе

(алгоритм фронта волны).

1) Помечаем вершину 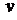индексом 0, затем помечаем вершины Î образу вершины 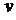индексом 1. Обозначаем их FW₁ (v). Полагаем k=1.

2) Если 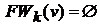или k=n-1, и одновременно 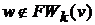то вершина 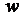не достижима из 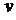. Работа алгоритма заканчивается.

В противном случае продолжаем:

3) Если 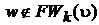, то переходим к шагу 4.

В противном случае мы нашли минимальный путь из 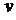в 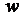и его длина равна k. Последовательность вершин

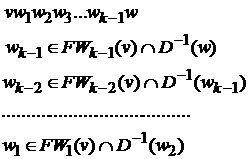
есть этот минимальный путь. Работа завершается.

4) Помечаем индексом k+1 все непомеченные вершины, которые принадлежат образу множества вершин c индексом k. Множество вершин с индексом k+1 обозначаем 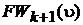. Присваиваем k:=k+1 и переходим к 2).

Замечания

· Множество 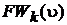называется фронтом волны k^го уровня.

· Вершины 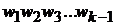могут быть выделены неоднозначно, что соответствует случаю, если 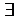несколько минимальных путей из 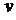в .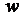

Чтобы найти расстояния в ориентированном графе, необходимо составить матрицу минимальных расстояний R(D)между его вершинами. Это квадратная матрица размерности 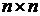, элементы главной диагонали которой равны нулю ( 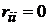, i=1,..,n).

Сначала составляем матрицу смежности. Затем переносим единицы из матрицы смежности в матрицу минимальных расстояний ( 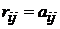, если 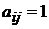). Далее построчно заполняем матрицу следующим образом.

Рассматриваем первую строку, в которой есть единицы. Пусть это строка − i-тая и на пересечении с j-тым столбцом стоит единица (то есть 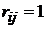). Это значит, что из вершины 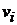можно попасть в вершину 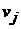за один шаг. Рассматриваем j-тую сроку (строку стоит вводить в рассмотрение, если она содержит хотя бы одну единицу). Пусть элемент 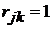. Тогда из вершины 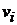в вершину 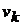можно попасть за два шага. Таким образом, можно записать 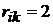. Следует заметить, что если в рассматриваемых строках две или более единиц, то следует прорабатывать все возможные варианты попадания из одной вершины в другую, записывая в матрицу длину наикратчайшего из них.

Примечание: В контрольной работе самый длинный путь найти при помощи алгоритма фронта волны.

Пример

Найдем расстояния в ориентированном графе D, изображенном на рис. 7. В данной задаче количество вершин n=7, следовательно, матрицы смежности и минимальных расстояний между вершинами ориентированного графа D будут иметь размерность 7×7.

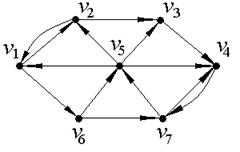
Рис.7.

Матрица смежности:

.

Начинаем заполнять матрицу R(D) минимальных расстояний: сначала ставим нули по главной диагоналии r_ij=a_ij, если a_ij=1, (т.е. переносим единицы из матрицы смежности). Рассматриваем первую строку. Здесь есть две единицы, то есть из первой вершины за один шаг можно попасть во вторую и шестую. Из второй вершины можно попасть за один шаг в третью (путь в первую вершину нас не интересует), следовательно, можно записать 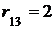. Из шестой вершины можем добраться за один шаг в пятую и седьмую, а значит, 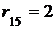, 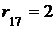. Теперь ищем маршруты, исходящие из первой вершины, состоящие из 3 шагов: за 2 шага идем в третью вершину, оттуда за один шаг попадаем в четвертую, поэтому 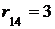. В итоге получаем следующую матрицу:

Таким образом, диаметром исследуемого ориентированного графа будет .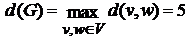

Для каждой вершины заданного ориентированного графа найдем максимальное удаление (эксцентриситет) в графе G от вершины нее по формуле, которая была приведена выше 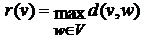: r(v_i) − максимальное из расстояний, стоящих в i-той строке. Таким образом,

r(v₁)=3, r(v₂)=3, r(v₃)=5, r(v₄)=4, r(v₅)=2, r(v₆)=2, r(v₇)=3.

Значит, радиусомграфа G будет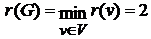

Соответственно, центрами графа G будут вершины v₅ и v₆ , так как величины их эксцентриситетов совпадают с величиной радиуса .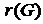

Опишем теперь нахождение минимального пути из вершины v₃ в вершину v₆ по алгоритму фронта волны. Обозначим вершину v₃ как V₀, а вершину v₆ - как W (см. рис. 8). Множество вершин, принадлежащих образу V₀, состоит из одного элемента - это вершина v₄, которую, согласно алгоритму, обозначаем как V₁: FW₁(v₃)={v₄}. Поскольку искомая вершина не принадлежит фронту волны первого уровня 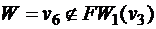, продолжаем работу алгоритма. Строим фронт волны второго уровня - это множество вершин, принадлежащих образу вершины V₁: FW₂(v₃)={v₇}, обозначаем v₇≡V₂. В образ вершины V₂ входят две вершины - v₅ и v₄, но, так как v₄ уже была помечена как V₀, то фронт волны третьего уровня состоит из одного элемента: FW₃(v₃)={v₅}, v₅≡V₃. Из непомеченных вершин в образ вершины V₃ входят v₁ и v₂, соответственно, FW₄(v₃)={v₁, v₂}, v₁≡V₄, v₂≡V₄. Теперь помечены все вершины, кроме v₆, которая входит в образ вершины 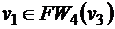, то есть FW₅(v₃)={v₆≡W}, работа алгоритма закончена. Минимальный путь (5 шагов) из вершины v₃ в вершину v₆ выглядит так: v₃ v₄ v₇ v₅ v₁ v₆.

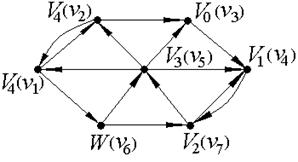
Рис.8.

Задание 3. Минимальный путь в нагруженном ориентированном графе

Найти минимальный путь в нагруженном ориентированном графе из вершины 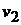в вершину 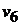по методу Форда-Беллмана.

Рассмотрим сначала общую задачу – нахождения минимального пути из вершины v_нач в v_кон.

Пусть D=(V,X) – нагруженный ориентированный граф, V={v₁,…,v_n}, n>1. Введем величины 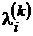, где i=1,…,n, k=0,1,2,…,n–1.

Для каждого фиксированного i и k величина 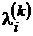равна длине минимального пути среди путей из v_нач в v_i содержащих не более k дуг. Если путей нет, то .

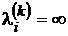Положим также .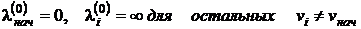

Составляем матрицу длин дуг C(D)=[c_ij] порядка n:

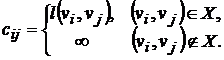
Утверждение. При i=2,…,n, k³0 выполняется равенство

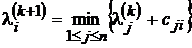. (3.1)

Алгоритм Форда-Беллмана нахождения минимального пути в нагруженном ориентированном графе D из v_нач в v_кон.( v_нач ≠ v_кон).

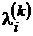( записываем в виде матрицы, i- строка, k-столбец).

1) Составляем таблицу 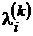, i=1,…,n, k=0,…,n-1. Если 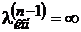, то пути из v_нач в v_кон нет. Конец алгоритма.

2) Если 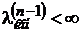то это число выражает длину любого минимального пути из v_нач в v_кон. Найдем минимальное k₁³1, при котором 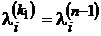. По определению 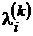получим, что k₁- минимальное число дуг в пути среди всех минимальных путей из v_нач в v_кон.

3) Затем определяем номера i₂,…, 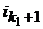такие, что

,

,

,

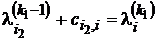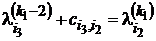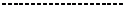
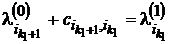то есть восстанавливаем по составленной таблице и матрице стоимости искомый минимальный путь из v_нач в v_кон.

Пример

Найдем минимальный путь из вершины v₂ в v₆ в ориентированном нагруженном графе D, изображенном на рис. 9. В рассматриваемом графе количество вершин n=7, следовательно, матрица длин дуг ориентированного графа D будет иметь размерность 7×7.

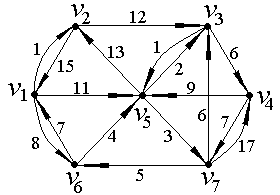
Рис. 9.

Матрица длин дуг для рассматриваемого графа будет выглядеть следующим образом:

.

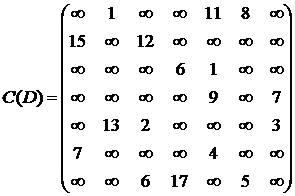Согласно алгоритму, составляем таблицу стоимости минимальных путей из вершины v₂ в вершину v_i не более, чем за k шагов, k=0,…n-1 (n=7, следовательно, k=0,…6). Как было определено выше, 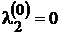, и 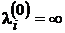для всех остальных вершин v_i ≠ v₂, то есть первый столбец таблицы состоит из элементов, равных 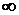, кроме элемента 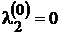. Второй столбец таблицы повторяет вторую строку матрицы стоимости, поскольку представляет собой стоимость возможных путей из вершины v₂ за один шаг. Далее по формуле (3.1) находим по столбцам все оставшиеся элементы таблицы. Например, чтобы найти элемент 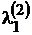, складываем элементы столбца 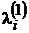и первого столбца матрицы стоимости и выбираем минимальное из получившихся чисел: .

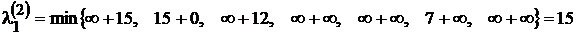В конечном итоге получаем следующую таблицу:

Теперь необходимо по построенной таблице и по матрице C(D) восстановить минимальный путь из вершины v₂ в v₆, который будет строиться с конца, то есть, начиная с вершины v6. Для этого выбираем минимальное из чисел, стоящих в строке, соответствующей v₆ в таблице. Это число – 21 – длина минимального искомого пути. В первый раз такая длина была получена при количестве шагов, равном 4. В вершину v₆ мы можем попасть за один шаг из вершин v₁ и v₇ (длина соответствующих дуг 8 и 5 соответственно – данные из матрицы C(D)). Выбираем минимальную по длине из этих дуг. Далее, в вершину v₇ можно попасть из v₄ и v₅(длина соответствующих дуг 7 и 3 соответственно). Продолжая аналогичным образом, найдем искомый путь за 4 шага минимальной длины из вершины v₂ в v₆: v₂ v₃ v₅ v₇ v₆.

Задание 4. Эйлеровы циклы и цепи

Найти Эйлерову цепь в неориентированном графе.

Исходя из утверждений 1 и 2, чтобы найти Эйлерову цепь, нужно соединить две вершины с нечетными степенями фиктивным ребром. Тогда задача сводится к нахождению Эйлерова цикла по приведенному ниже алгоритму. Из найденного цикла удаляется фиктивное ребро, тем самым находится искомая Эйлерова цепь.