Справочный материал к выполнению контрольной работы №1
Оглавление
Стр.
Введение. 4
Задания для выполнения контрольных работ. 5
1. Задания на контрольную работу «Функции комплексной переменной». 5
СоДЕРЖАНИЕ теоретического материала и ссылки на литературу 6
Справочный материал к выполнению контрольной работы №1 7
2. Функции комплексной переменной.. 11
2.1. Определение и свойства функции комплексной переменной. 11
2.2. Дифференцирование ФКП. Аналитические ФКП.. 12
Рекомендуемая литература.. 17
Введение
Настоящее пособие предназначено для студентов 2 курса, обучающихся по техническим специальностям. В пособии содержатся задания к выполнению контрольных работ по темам «Комплексные числа. Функции комплексной переменной», а также ссылки на теоретический материал, необходимый для выполнения этих контрольных работ и список рекомендуемой литературы. В результате изучения этих тем студенты должны:
• знать, что такое мнимая единица и комплексное число, уметь производить операции над комплексными числами в алгебраической и тригонометрической формах;
• уметь решать простейшие алгебраические уравнения на множестве комплексных чисел;
• иметь представление о функции комплексной переменной, об ее аналитичности и уметь дифференцировать аналитические функции комплексной переменной;
Данные методические рекомендации включают также справочный материал, необходимый для выполнения контрольной работы по перечисленным темам, и решения примерного варианта этой работы, в которых имеются ссылки на используемый справочный материал.
Задания для выполнения контрольных работ
Перед выполнением каждой контрольной работы необходимо изучить теоретический материал по данной теме и закрепить его решением рекомендованных задач в соответствии со ссылками на литературу, затем ознакомиться со справочным материалом и образцом выполнения примерного варианта контрольной работы.
Задания на контрольную работу «Функции комплексной переменной»
Контрольная работа состоит из двух задач. Задание для каждой задачи включает в себя ее формулировку и десять вариантов исходных данных.
Задача 1. Даны уравнение, комплексное число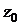 
и натуральное число n.
Требуется:
1) найти корни уравнения z1, z2 на множестве комплексных чисел;
2) найти комплексное число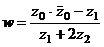 
в алгебраической форме;
3) получить тригонометрическую форму числа 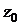и вычислить с ее помощью 
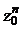. Ответ записать в тригонометрической и в алгебраической формах.
| № варианта | Уравнение | 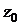| n |
 |  | ||
 |  | ||
 |  | ||
 |  | ||
 |  | ||
 |  | ||
 |  | ||
 |  | ||
 |  | ||
 |  |
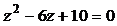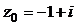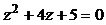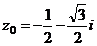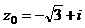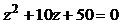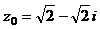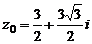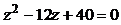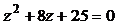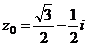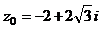Задача 2. Дана функция комплексной переменной (ФКП) w = f (z), где
z = x + iy, и точка z0. Требуется:
1) представить ФКП в виде w = u(x,y) +iv(x,y), выделив ее действительную и мнимую части;
2) проверить, является ли функция w аналитической;
3) в случае аналитичности функции w найти ее производную w′ в точке z0.
| № варианта | Функция w = f (z), точка z0 | № варианта | Функция w = f (z), точка z0 |
 |  | ||
 |  | ||
 |  | ||
 |  | ||
 |  |
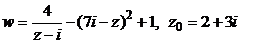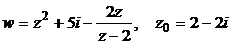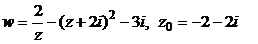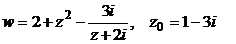СоДЕРЖАНИЕ теоретического материала и ссылки на литературу
| № темы | Содержание | Литература |
| Комплексные числа. Действия над комплексными числами в алгебраической и тригонометрической формах. Решение простейших алгебраических уравнений на множестве комплексных чисел | [1], гл. VI, § 27–28; [2], гл. 14, § 6.1; [4], гл. 9, № 1–52 | |
| Функции комплексной переменной (ФКП). Производная ФКП. Условия Коши-Римана (Эйлера-Даламбера). Аналитические функции комплексной переменной и их дифференцирование | [2], гл. VIII, § 28.1-28.5; [6], гл. VII , № 1012, 1013, 1028, 1029, 1033-1035; [8], гл. III, № 3.29, 3.32, 3.36, 3.37-3.39 |
Примечание. Ссылки на литературу в таблице даны в соответствии с номерами в списке рекомендуемой литературы.
Комплексные числа
Оглавление
Стр.
Введение. 4
Задания для выполнения контрольных работ. 5
1. Задания на контрольную работу «Функции комплексной переменной». 5
СоДЕРЖАНИЕ теоретического материала и ссылки на литературу 6
Справочный материал к выполнению контрольной работы №1 7
2. Функции комплексной переменной.. 11
2.1. Определение и свойства функции комплексной переменной. 11
2.2. Дифференцирование ФКП. Аналитические ФКП.. 12
Рекомендуемая литература.. 17
Введение
Настоящее пособие предназначено для студентов 2 курса, обучающихся по техническим специальностям. В пособии содержатся задания к выполнению контрольных работ по темам «Комплексные числа. Функции комплексной переменной», а также ссылки на теоретический материал, необходимый для выполнения этих контрольных работ и список рекомендуемой литературы. В результате изучения этих тем студенты должны:
• знать, что такое мнимая единица и комплексное число, уметь производить операции над комплексными числами в алгебраической и тригонометрической формах;
• уметь решать простейшие алгебраические уравнения на множестве комплексных чисел;
• иметь представление о функции комплексной переменной, об ее аналитичности и уметь дифференцировать аналитические функции комплексной переменной;
Данные методические рекомендации включают также справочный материал, необходимый для выполнения контрольной работы по перечисленным темам, и решения примерного варианта этой работы, в которых имеются ссылки на используемый справочный материал.
Задания для выполнения контрольных работ
Перед выполнением каждой контрольной работы необходимо изучить теоретический материал по данной теме и закрепить его решением рекомендованных задач в соответствии со ссылками на литературу, затем ознакомиться со справочным материалом и образцом выполнения примерного варианта контрольной работы.
Задания на контрольную работу «Функции комплексной переменной»
Контрольная работа состоит из двух задач. Задание для каждой задачи включает в себя ее формулировку и десять вариантов исходных данных.
Задача 1. Даны уравнение, комплексное число 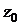и натуральное число n.
Требуется:
1) найти корни уравнения z1, z2 на множестве комплексных чисел;
2) найти комплексное число 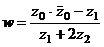в алгебраической форме;
3) получить тригонометрическую форму числа 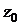и вычислить с ее помощью 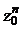. Ответ записать в тригонометрической и в алгебраической формах.
| № варианта | Уравнение | 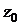| n |
| | | ||
| | | ||
| | | ||
| | | ||
| | | ||
| | | ||
| | | ||
| | | ||
| | | ||
| | |
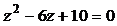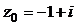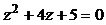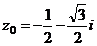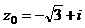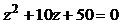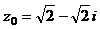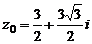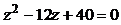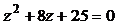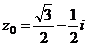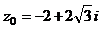Задача 2. Дана функция комплексной переменной (ФКП) w = f (z), где
z = x + iy, и точка z0. Требуется:
1) представить ФКП в виде w = u(x,y) +iv(x,y), выделив ее действительную и мнимую части;
2) проверить, является ли функция w аналитической;
3) в случае аналитичности функции w найти ее производную w′ в точке z0.
| № варианта | Функция w = f (z), точка z0 | № варианта | Функция w = f (z), точка z0 |
| | | ||
| | | ||
| | | ||
| | | ||
| | |
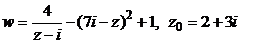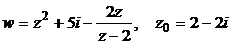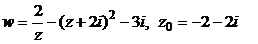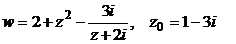СоДЕРЖАНИЕ теоретического материала и ссылки на литературу
| № темы | Содержание | Литература |
| Комплексные числа. Действия над комплексными числами в алгебраической и тригонометрической формах. Решение простейших алгебраических уравнений на множестве комплексных чисел | [1], гл. VI, § 27–28; [2], гл. 14, § 6.1; [4], гл. 9, № 1–52 | |
| Функции комплексной переменной (ФКП). Производная ФКП. Условия Коши-Римана (Эйлера-Даламбера). Аналитические функции комплексной переменной и их дифференцирование | [2], гл. VIII, § 28.1-28.5; [6], гл. VII , № 1012, 1013, 1028, 1029, 1033-1035; [8], гл. III, № 3.29, 3.32, 3.36, 3.37-3.39 |
Примечание. Ссылки на литературу в таблице даны в соответствии с номерами в списке рекомендуемой литературы.
Справочный материал к выполнению контрольной работы №1
Комплексные числа