А – функциональная схема; б – УГО

Полусумматоры и сумматоры

1.1. Классификация сумматоров

В настоящее время получили распространение схемы, в которых выходной сигнал формируется непосредственно в цифровой форме. Затем этот сигнал преобразуется в аналоговую форму при помощи цифроаналогового преобразователя. В составе этих микросхем широко используются сумматоры, умножители и цифровые фильтры.

Наиболее распространенной операцией в устройствах обработки цифровой информации является суммирование, т. е. арифметическое сложение двух чисел, имеющих одинаковое число разрядов. Операция сложения выполняется в соответствии с правилами арифметики, используемой в данном конкретном случае системы счисления.

Сумматоромназывают функциональный узел, выполняющий сложение одно- или многоразрядных двоичных чисел в соответствии с правилами двоичного сложения.

Многоразрядные сумматоры строятся на основе одноразрядных.

Сумматоры выполняют арифметическую операцию сложения двух чисел. Они имеют как самостоятельное значение, так и являются составной частью арифметическо-логических устройств (АЛУ), реализующих ряд разнообразных операций и являющихся непременной частью всех процессоров.

При организации различных вычислительных процессов суммированию отводится главная роль, оно является основной операцией. Например, вычитание – это суммирование с использованием ДК или ОК, умножение сводится к сдвигу и сложению (суммированию) двоичных чисел.

Следует отметить, что сумматоры являются логическими устройствами, функционируют по законам алгебры логики, но выполняют операцию арифметического, а не логического сложения.

В соответствии с определением, сумматор суммирует два числа. Выходной сигнал зависит только от двух входных сигналов, действующих на входе в текущий момент. Следовательно, сумматор является комбинационным устройством. Однако, некоторые сумматоры, например, накапливающий сумматор и другие, содержат в своем составе элементы памяти.

По числу выводов различают:

- полусумматоры;

- одноразрядные сумматоры;

- многоразрядные сумматоры.

Полусумматор имеет два входа и два выхода, предназначен для сложения двух одноразрядных слов и формирует на своих выходах сигнал суммы и сигнал переноса в старший разряд.

Одноразрядный сумматор имеет три входа и два выхода, предназначен для сложения двух одноразрядных слов и сигнала переноса из младшего разряда., формирует сигнал выхода и сигнал переноса в старший разряд.

Многоразрядный сумматор предназначен для сложения многоразрядных слов.

В настоящее время выпускают микросхемы одно-, двух- и четырехразрядные сумматоры. Маркировку микросхем – сумматоров можно определить по буквам ИМ – функциональное назначение, например, К555ИМ6 – четырехразрядный полный двоичный сумматор. На принципиальных схемах сумматоры обозначают буквами SM.

В зависимости от способа обработки чисел различают многоразрядные сумматоры:

- последовательного;

- параллельного;

- последовательно-параллельного действия.

В последовательных сумматорах сложение чисел осуществляется поразрядно, последовательно во времени.

В параллельных сумматорах действия сложение всех разрядов многоразрядных чисел происходит одновременно.

По способу тактирования различают сумматоры:

- синхронные;

- асинхронные.

В синхронных сумматорах операция сложения осуществляется по тактовым импульсам, и время ее проведения не зависит от длины разрядов кодов, остается постоянным.

В асинхронных сумматорах время выполнения операции зависит от длины входных кодов и поэтому необходимо формировать признак окончания операции.

В зависимости от используемой системы счисления различают сумматоры:

- двоичные;

- двоично-десятичные и др.

Аппаратная сложность и быстродействие сумматора являются очень важными параметрами и поэтому разработано множество вариантов сумматоров, которые имеют разветвленную классификацию. В виду особой важности на основе различных алгоритмов синтеза разработано большое количество разнообразных схем сумматоров:

- одноразрядный сумматор;

- сумматор для последовательных операндов;

- сумматор для параллельных операндов с последовательным переносом;

- сумматор для параллельных операндов с параллельным переносом;

- сумматор с последовательным распространением переноса по цепочке замкнутых ключей;

- сумматор групповой структуры с цепным переносом;

- сумматор групповой структуры с параллельным межгрупповым переносом;

- сумматор с условным переносом;

- накапливающий сумматор.

Наряду с сумматорами могут быть реализованы вычитатели, однако это почти никогда не делается, поскольку вычитание выполняется посредством сложения с применением ДК либо ОК.

Кроме параметров, определяющих условия эксплуатации сумматоров как микросхем, используют следующие параметры, необходимые при решении задачи синтеза электрических схем устройства обработки цифровой информации на основе сумматоров:

- разрядность;

- способ суммирования двоичных чисел (последовательный или параллельный);

- тип входной логики сумматора по входу и по входу ;

- наличие и организация входов управления;

- способ организации цепи переноса;

- тип выходной логики;

- быстродействие (время задержки сигнала и переноса);

- потребляемый ток питания;

- особенности монтажа при увеличении разрядности сумматора.

Подробно вопросы двоичной арифметики будут освещены в лекции № 22. Рассмотрим наиболее характерные схемы построения сумматоров.

1.2.Одноразрядный полусумматор

В сумматорах операция суммирования чисел, представленных в двоичном коде, осуществляется поразрядно.

Простейший случай – это суммирование двух одноразрядных слов. В десятичной системе

(14.1)

что соответствует в двоичной системе счисления

(14.2)

В последнем случае результат суммы оказался двухразрядным 10₂ = 2₁₀. Обычное явление, когда при суммировании двух чисел в любой системе счисления результат имеет на один разряд больше. В двоичной системе единица в старшем разряде суммы называется единицей переноса. Сведем формулы (14.2) в таблицу 14.1.

Таблица 14.1 – Таблица истинности полусумматора

Слагаемые	Сумма S	Перенос Р	Математическое выражение
				0+0 = 010 (002)
				0+1 = 110 (012)
				1+0=110 (012)
				1+1 =210 (102)

Обратите внимание,что сигналы в приведенной таблице истинности расположены в порядке, принятом для схем, т. е. в соответствии с тем, что сигнал распространяется слева направо. В результате перенос, который имеет двоичный вес больший, по сравнению с суммируемыми разрядами, записан правее. В математике принят другой порядок разрядов числа. Старший разряд на бумаге записывается самым левым, а младший разряд – самым правым. В результате может возникнуть путаница. Чтобы этого не произошло, введен десятичный эквивалент каждой строки таблицы истинности полусумматора (таблица 14.1).

Из таблицы 14.1 получим аналитические выражения для суммы S и переноса Р. Выражение для Sможно записать с помощью известной операции ИСКЛЮЧАЮЩЕЕ-ИЛИ

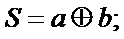(14.3)

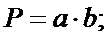(14.4)

Техническая реализация полусумматора на основе формул (14.3) и (14.4) представлена на рисунке 14.1.

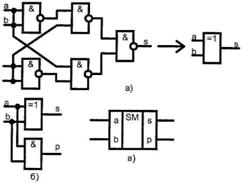
Рисунок 14.1 – Схема полусумматора в базисе И-НЕ (сумматор по модулю 2):

а, б – функциональные схемы; в – УГО; г) УГО схемы «исключающее ИЛИ»

Используя представление в базисе ИЛИ-НЕ,из таблицы 14.1 получим

(14.5)

На основе формулы (14.5) построим схему полусумматора, содержащего меньшее число логических элементов (рисунок 14.2). В то же время схема содержит различные элементы: И, НЕ, ИЛИ.

Рисунок 14.2 – Схема полусумматора в базисе ИЛИ-НЕ

Полусумматор (см. рисунки 14.1; 14.2) не имеет входа переноса с предыдущего разряда, поэтому его можно использовать только в младших разрядах устройства обработки многоразрядных двоичных слов.

Полусумматоры выпускаются в виде отдельных микросхем и используются в качестве отдельных модулей в составе больших интегральных микросхем, поэтому ГОСТом предусмотрено УГО полусумматора. Оно приведено на рисунке (см. рисунок 14.1 в).

Полусумматор формирует перенос в следующий разряд, но не может учитывать перенос из предыдущего разряда, поэтому он и называется полусумматором. В результате такой особенности полусумматор не может использоваться в качестве отдельного устройства.

Интегральные схемы полусумматоров обозначаются "ИЛ". Например, 155ИЛ7 – полусумматор.

Практический интерес представляет полный сумматор.

Сумматор по модулю 2 выполняет суммирование без учета переноса между двоичными разрядами.В полном двоичном сумматоре его необходимо учитывать, поэтому требуются элементы, позволяющие формировать перенос в следующий двоичный разряд.

1.3.Одноразрядный комбинационный сумматор

Одноразрядным комбинационным сумматоромназывают операционный элемент, выполняющий микрооперацию суммирования двух или нескольких одноразрядных чисел.

Таблицу истинности полного одноразрядного двоичного сумматора (таблица 20.2), можно получить из правил арифметического суммирования двоичных чисел. В обозначении входов и выходов полного сумматора использовано следующее правило: в качестве входов использованы одноразрядные двоичные числа 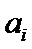и 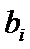; сумма – это одноразрядное двоичное число ; перенос обозначен буквой 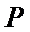; для обозначения входа переноса используется сочетание букв (i – сокращение от английского слова input, вход) или (РI); для обозначения выхода переноса используется сочетание букв или РО (О – сокращение от английского слова output,выход).

Правила двоичного сложения одноразрядного сумматора можно представить в виде таблицы истинности (таблица 14.2) будущей логической схемы двоичного сумматора и построить эту схему по ранее изложенным принципам.

Для текущего разряда суммы логическое выражение имеет вид:

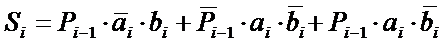
причем согласно карте Карно, представленной на рисунке 20.3 а, данное выражение не минимизируется. Для выходного переноса минимизация возможна, поэтому логическое выражение согласно рисунку 14.3 б, получается следующим:

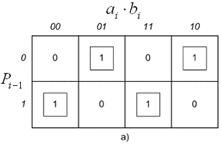Рисунок 14.3 – Карты Карно для одноразрядного сумматора: а – для текущего разряда суммы; б – для текущего разряда выходного переноса

Схема одноразрядного сумматора и его УГО представлены на рисунке 14.4.

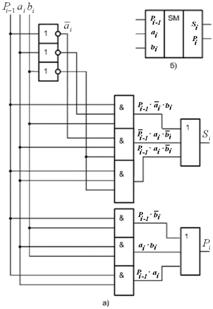
Рисунок 14.4 – Одноразрядный сумматор:

Цифровые умножители

Следующим, широко используемым в схемах цифровой обработки сигналов устройством, является цифровой двоичный умножитель. Эти устройства используются как в схемах масштабирования (усилители или аттенюаторы) или гетеродинирования сигналов, так и в составе цифровых фильтров.

Умножение чисел в двоичном виде производится подобно умножению в десятичной системе счисления. При реализации этого алгоритма потребуется перемножить каждый разряд множимого на соответствующий разряд множителя.

Рассмотрим в качестве примера умножение двух четырехразрядных двоичных чисел. Пусть требуется умножить число 1011₂ (11₁₀) на число 1101₂ (13₁₀). В результате умножения мы ожидаем получить число 10001111₂ (143₁₀). Выполним операцию умножения в столбик в двоичной системе, как это показано на рисунке 14.11.

Для формирования произведения требуется вычислить четыречастичных произведения. Обратите внимание,что в двоичной арифметике требуется выполнять умножение только на числа 0 и 1. Это означает, что нужно либо суммировать множимое к сумме остальных частичных произведений, либо нет. В результате для формирования частичного произведения можно воспользоваться логическими элементами "2И", подключенными к каждому двоичному разряду множимого.

Для формирования частичного произведения, кроме операции умножения на один разряд, требуется осуществлять его сдвиг влево на число разрядов, соответствующее весу разряда множителя. Сдвиг можно осуществить простым соединением соответствующих разрядов частичных произведений к необходимым разрядам двоичного сумматора.

Рисунок 14.11 – Выполнение операции умножения

Двоичных чисел в столбик

Для того чтобы принципиальная схема умножителя была похожа на пример двоичного умножения, приведенный на рисунке 14.11, используем УГО микросхем, где входы расположены сверху, а выходы снизу. Это разрешено ГОСТом. В полном соответствии с алгоритмом умножения в столбик нам потребуются три четырехразрядных сумматора.

Принципиальная схема умножителя, реализующая алгоритм двоичного умножения в столбик, приведена на рисунке 14.12.

Формирование частичных произведений в этой схеме осуществляют цифровые микросхемы D1, D3. D5 и D7. В этих микросхемах в одном корпусе содержится сразу четыре логических элемента "2И".

Сумматор, выполненный на микросхеме D6, суммирует первое и второе частные произведения. При этом младший разряд первого частного произведения не нуждается в суммировании. Поэтому он подается на выход умножителя непосредственно (разряд М0).

Второе частное произведение должно быть сдвинуто на один разряд. Это осуществляется тем, что младший разряд выходного числа сумматора D6 соединяется со вторым разрядом произведения (M l). Но тогда первое частное произведение необходимо сдвинуть на один разряд влево по отношению ко второму частному произведению!

Это арифметическое действие выполняется за счет того, что младший разряд группы входов А соединяется с первым разрядом частного произведения, первый разряд группы входов А соединяется со вторым разрядом частного произведения, и т. д. Однако старший разряд группы входов А не с чем соединять!

Для того чтобы разрешить это противоречие вспомним, что если записать слева от числа ноль, то значение исходного числа не изменится, поэтому мы должны этот разряд соединить с общим проводом схемы, добавляя тем самым ноль в старший разряд первого частного произведения.

Точно таким же образом осуществляется суммирование к результату третьего и четвертого частного произведения. Эту операцию выполняют микросхемы D4 и D2 соответственно. Отличие в построении схемы заключается только в том, что здесь не нужно задумываться о старшем разряде предыдущей суммы, ведь предыдущая микросхема сумматора формирует сигнал переноса для последующей микросхемы.

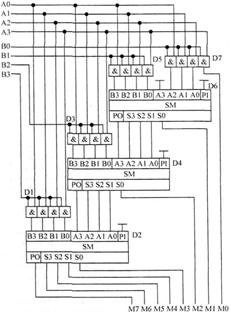
Рисунок 14.12 – Принципиальная схема матричного умножителя 4 на 4

Если внимательно посмотреть на схему умножителя, приведенную на рисунке 14.12, то можно увидеть, что она образует матрицу, сформированную цепями, по которым передаются разряды числа А и числа В. В точках пересечения этих цепей находятся логические элементы "2И". Именно по этой причине умножители, реализованные по данной схеме, получили название матричных умножителей.

Скорость работы схемы, приведенной на рисунке 14.12, определяется максимальным временем распространения сигнала по самому длинному пути. Это путь, проходящий через микросхемы D7, D6, D4, D2. Время работы схемы можно сократить, если сумматоры располагать не последовательно друг за другом, как это предполагается алгоритмом двоичного умножения (пример умножения приведен на рисунке 14.11), а суммировать частичные произведения попарно, затем суммировать пары частичных произведений и т. д. В этом случае время выполнения операции умножения значительно сократится.

Особенно заметен выигрыш в быстродействии при построении многоразрядных умножителей. Однако ничего не бывает бесплатно. В обмен на увеличение быстродействия придется заплатить увеличением разрядности сумматоров, а значит, сложностью схемы. Если сумматоры частных произведений останутся той же разрядности, что и ранее, то разрядность сумматоров пар частичных произведений должна быть увеличена на единицу.

Разрядность сумматоров четверок частичных произведений будет на два разряда больше разрядности сумматоров частичных произведений, т. к. при суммировании четырех чисел их значение в наиболее неблагоприятном случае может увеличиться в четыре раза, и т. д.

Цифровые матричные умножители широко применяются в схемах обработки сигналов для изменения коэффициента передачи устройства, для реализации преобразователей частоты, и как составляющая часть цифровых фильтров.

Полусумматоры и сумматоры

1.1. Классификация сумматоров

В настоящее время получили распространение схемы, в которых выходной сигнал формируется непосредственно в цифровой форме. Затем этот сигнал преобразуется в аналоговую форму при помощи цифроаналогового преобразователя. В составе этих микросхем широко используются сумматоры, умножители и цифровые фильтры.

Наиболее распространенной операцией в устройствах обработки цифровой информации является суммирование, т. е. арифметическое сложение двух чисел, имеющих одинаковое число разрядов. Операция сложения выполняется в соответствии с правилами арифметики, используемой в данном конкретном случае системы счисления.

Сумматоромназывают функциональный узел, выполняющий сложение одно- или многоразрядных двоичных чисел в соответствии с правилами двоичного сложения.

Многоразрядные сумматоры строятся на основе одноразрядных.

Сумматоры выполняют арифметическую операцию сложения двух чисел. Они имеют как самостоятельное значение, так и являются составной частью арифметическо-логических устройств (АЛУ), реализующих ряд разнообразных операций и являющихся непременной частью всех процессоров.

При организации различных вычислительных процессов суммированию отводится главная роль, оно является основной операцией. Например, вычитание – это суммирование с использованием ДК или ОК, умножение сводится к сдвигу и сложению (суммированию) двоичных чисел.

Следует отметить, что сумматоры являются логическими устройствами, функционируют по законам алгебры логики, но выполняют операцию арифметического, а не логического сложения.

В соответствии с определением, сумматор суммирует два числа. Выходной сигнал зависит только от двух входных сигналов, действующих на входе в текущий момент. Следовательно, сумматор является комбинационным устройством. Однако, некоторые сумматоры, например, накапливающий сумматор и другие, содержат в своем составе элементы памяти.

По числу выводов различают:

- полусумматоры;

- одноразрядные сумматоры;

- многоразрядные сумматоры.

Полусумматор имеет два входа и два выхода, предназначен для сложения двух одноразрядных слов и формирует на своих выходах сигнал суммы и сигнал переноса в старший разряд.

Одноразрядный сумматор имеет три входа и два выхода, предназначен для сложения двух одноразрядных слов и сигнала переноса из младшего разряда., формирует сигнал выхода и сигнал переноса в старший разряд.

Многоразрядный сумматор предназначен для сложения многоразрядных слов.

В настоящее время выпускают микросхемы одно-, двух- и четырехразрядные сумматоры. Маркировку микросхем – сумматоров можно определить по буквам ИМ – функциональное назначение, например, К555ИМ6 – четырехразрядный полный двоичный сумматор. На принципиальных схемах сумматоры обозначают буквами SM.

В зависимости от способа обработки чисел различают многоразрядные сумматоры:

- последовательного;

- параллельного;

- последовательно-параллельного действия.

В последовательных сумматорах сложение чисел осуществляется поразрядно, последовательно во времени.

В параллельных сумматорах действия сложение всех разрядов многоразрядных чисел происходит одновременно.

По способу тактирования различают сумматоры:

- синхронные;

- асинхронные.

В синхронных сумматорах операция сложения осуществляется по тактовым импульсам, и время ее проведения не зависит от длины разрядов кодов, остается постоянным.

В асинхронных сумматорах время выполнения операции зависит от длины входных кодов и поэтому необходимо формировать признак окончания операции.

В зависимости от используемой системы счисления различают сумматоры:

- двоичные;

- двоично-десятичные и др.

Аппаратная сложность и быстродействие сумматора являются очень важными параметрами и поэтому разработано множество вариантов сумматоров, которые имеют разветвленную классификацию. В виду особой важности на основе различных алгоритмов синтеза разработано большое количество разнообразных схем сумматоров:

- одноразрядный сумматор;

- сумматор для последовательных операндов;

- сумматор для параллельных операндов с последовательным переносом;

- сумматор для параллельных операндов с параллельным переносом;

- сумматор с последовательным распространением переноса по цепочке замкнутых ключей;

- сумматор групповой структуры с цепным переносом;

- сумматор групповой структуры с параллельным межгрупповым переносом;

- сумматор с условным переносом;

- накапливающий сумматор.

Наряду с сумматорами могут быть реализованы вычитатели, однако это почти никогда не делается, поскольку вычитание выполняется посредством сложения с применением ДК либо ОК.

Кроме параметров, определяющих условия эксплуатации сумматоров как микросхем, используют следующие параметры, необходимые при решении задачи синтеза электрических схем устройства обработки цифровой информации на основе сумматоров:

- разрядность;

- способ суммирования двоичных чисел (последовательный или параллельный);

- тип входной логики сумматора по входу и по входу ;

- наличие и организация входов управления;

- способ организации цепи переноса;

- тип выходной логики;

- быстродействие (время задержки сигнала и переноса);

- потребляемый ток питания;

- особенности монтажа при увеличении разрядности сумматора.

Подробно вопросы двоичной арифметики будут освещены в лекции № 22. Рассмотрим наиболее характерные схемы построения сумматоров.

1.2.Одноразрядный полусумматор

В сумматорах операция суммирования чисел, представленных в двоичном коде, осуществляется поразрядно.

Простейший случай – это суммирование двух одноразрядных слов. В десятичной системе

(14.1)

что соответствует в двоичной системе счисления

(14.2)

В последнем случае результат суммы оказался двухразрядным 10₂ = 2₁₀. Обычное явление, когда при суммировании двух чисел в любой системе счисления результат имеет на один разряд больше. В двоичной системе единица в старшем разряде суммы называется единицей переноса. Сведем формулы (14.2) в таблицу 14.1.

Таблица 14.1 – Таблица истинности полусумматора

Слагаемые	Сумма S	Перенос Р	Математическое выражение
				0+0 = 010 (002)
				0+1 = 110 (012)
				1+0=110 (012)
				1+1 =210 (102)

Обратите внимание,что сигналы в приведенной таблице истинности расположены в порядке, принятом для схем, т. е. в соответствии с тем, что сигнал распространяется слева направо. В результате перенос, который имеет двоичный вес больший, по сравнению с суммируемыми разрядами, записан правее. В математике принят другой порядок разрядов числа. Старший разряд на бумаге записывается самым левым, а младший разряд – самым правым. В результате может возникнуть путаница. Чтобы этого не произошло, введен десятичный эквивалент каждой строки таблицы истинности полусумматора (таблица 14.1).

Из таблицы 14.1 получим аналитические выражения для суммы S и переноса Р. Выражение для Sможно записать с помощью известной операции ИСКЛЮЧАЮЩЕЕ-ИЛИ

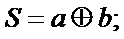(14.3)

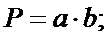(14.4)

Техническая реализация полусумматора на основе формул (14.3) и (14.4) представлена на рисунке 14.1.

Рисунок 14.1 – Схема полусумматора в базисе И-НЕ (сумматор по модулю 2):

а, б – функциональные схемы; в – УГО; г) УГО схемы «исключающее ИЛИ»

Используя представление в базисе ИЛИ-НЕ,из таблицы 14.1 получим

(14.5)

На основе формулы (14.5) построим схему полусумматора, содержащего меньшее число логических элементов (рисунок 14.2). В то же время схема содержит различные элементы: И, НЕ, ИЛИ.

Рисунок 14.2 – Схема полусумматора в базисе ИЛИ-НЕ

Полусумматор (см. рисунки 14.1; 14.2) не имеет входа переноса с предыдущего разряда, поэтому его можно использовать только в младших разрядах устройства обработки многоразрядных двоичных слов.

Полусумматоры выпускаются в виде отдельных микросхем и используются в качестве отдельных модулей в составе больших интегральных микросхем, поэтому ГОСТом предусмотрено УГО полусумматора. Оно приведено на рисунке (см. рисунок 14.1 в).

Полусумматор формирует перенос в следующий разряд, но не может учитывать перенос из предыдущего разряда, поэтому он и называется полусумматором. В результате такой особенности полусумматор не может использоваться в качестве отдельного устройства.

Интегральные схемы полусумматоров обозначаются "ИЛ". Например, 155ИЛ7 – полусумматор.

Практический интерес представляет полный сумматор.

Сумматор по модулю 2 выполняет суммирование без учета переноса между двоичными разрядами.В полном двоичном сумматоре его необходимо учитывать, поэтому требуются элементы, позволяющие формировать перенос в следующий двоичный разряд.

1.3.Одноразрядный комбинационный сумматор

Одноразрядным комбинационным сумматоромназывают операционный элемент, выполняющий микрооперацию суммирования двух или нескольких одноразрядных чисел.

Таблицу истинности полного одноразрядного двоичного сумматора (таблица 20.2), можно получить из правил арифметического суммирования двоичных чисел. В обозначении входов и выходов полного сумматора использовано следующее правило: в качестве входов использованы одноразрядные двоичные числа 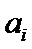и 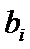; сумма – это одноразрядное двоичное число ; перенос обозначен буквой 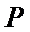; для обозначения входа переноса используется сочетание букв (i – сокращение от английского слова input, вход) или (РI); для обозначения выхода переноса используется сочетание букв или РО (О – сокращение от английского слова output,выход).

Правила двоичного сложения одноразрядного сумматора можно представить в виде таблицы истинности (таблица 14.2) будущей логической схемы двоичного сумматора и построить эту схему по ранее изложенным принципам.

Для текущего разряда суммы логическое выражение имеет вид:

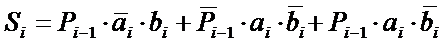
причем согласно карте Карно, представленной на рисунке 20.3 а, данное выражение не минимизируется. Для выходного переноса минимизация возможна, поэтому логическое выражение согласно рисунку 14.3 б, получается следующим:

Рисунок 14.3 – Карты Карно для одноразрядного сумматора: а – для текущего разряда суммы; б – для текущего разряда выходного переноса

Схема одноразрядного сумматора и его УГО представлены на рисунке 14.4.

Рисунок 14.4 – Одноразрядный сумматор:

а – функциональная схема; б – УГО

Теперь, точно так же, как и в предыдущих случаях, в соответствии с правилами построения принципиальной схемы по произвольной таблице истинности получим схему полного двоичного одноразрядного сумматора, построенной на базе ИМС. Схема приведены на рисунках 14.5 и 14.6.

Примером одноразрядного двоичного сумматора может служить микросхема средней интеграции К155ИМ1. Обычно для выполнения вычислений в схемах цифровой обработки сигналов недостаточно точности одноразрядного сумматора. В них применяются 16- или даже 40-разрядные двоичные сумматоры.

Рисунок 14.5 – Схема полного двоичного одноразрядного сумматора	Рисунок 14.6 – Минимизированнаясхема полного двоичного одноразрядного сумматора