Алгебраические фракталы: метод построения алгебраических фракталов.
Свое название эти фракталы получили за то, что их строят на основе алгебраических формул.
Примеры: множество Мандельброта, множество Жюлиа, фрактал Ньютона.
Метод:
1. Выбирается формула (функция), в нее подставляется число и получается результат.
2. Полученный результат подставляется в эту же формулу и получается следующее число.
3. Повторение процедуры.
4. Получается набор чисел, являющихся точками фрактала.
Функция для разных точек может иметь разное поведение:
1. Стремится к бесконечности.
2. Стремится к 0.
3. Принимает несколько фиксированных значений.
4. Хаотичное поведение.
24 вопрос. Множество Мандельброта (один из самых известных фрактальных объектов) впервые было построено (визуально с применением ЭВМ) Бенуа Мандельбротом весной 1980 г. в исследовательском центре фирмы IBM им. Томаса Дж. Уотсона. И хотя исследования подобных объектов начались ещё в прошлом веке, именно открытие этого множества и совершенствование аппаратных средств машинной графики в решающей степени повлияли на развитие фрактальной геометрии и теории хаоса. Итак, что же такое множество Мандельброта.
Рассмотрим функцию комплексного переменного 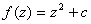 . Положим
. Положим 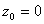 и рассмотрим последовательность
и рассмотрим последовательность 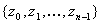 , где для любого
, где для любого 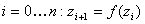 . Такая последовательность может быть ограниченной (т.е. может существовать такое r, что для любого
. Такая последовательность может быть ограниченной (т.е. может существовать такое r, что для любого 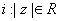 ) либо "убегать в бесконечность" (т.е. для любого r > 0существует
) либо "убегать в бесконечность" (т.е. для любого r > 0существует 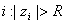 ). Множество Мандельброта можно определить как множество комплексных чисел c, для которых указанная последовательность является ограниченной. К сожалению, не известно аналитического выражения, которое позволяло бы по данному c определить, принадлежит ли оно множеству Мандельброта или нет. Поэтому для построения множества используют компьютерный эксперимент: просматривают с некоторым шагом множество точек на комплексной плоскости, для каждой точки проводят определённое число итераций (находят определённое число членов последовательности) и смотрят за её "поведением". (Рис. 4).
). Множество Мандельброта можно определить как множество комплексных чисел c, для которых указанная последовательность является ограниченной. К сожалению, не известно аналитического выражения, которое позволяло бы по данному c определить, принадлежит ли оно множеству Мандельброта или нет. Поэтому для построения множества используют компьютерный эксперимент: просматривают с некоторым шагом множество точек на комплексной плоскости, для каждой точки проводят определённое число итераций (находят определённое число членов последовательности) и смотрят за её "поведением". (Рис. 4).
Доказано, что множество Мандельброта размещается в круге радиуса r=2 с центром в начале координат. Таким образом, если на некотором шаге модуль очередного члена последовательности превышает 2, можно сразу сделать вывод, что точка, соответствующая c, определяющему данную последовательность, не принадлежит множеству Мандельброта.
Уменьшая шаг, с которым просматриваются комплексные числа, и увеличивая количество итераций, мы можем получать сколь угодно подробные, но всегда лишь приближённые изображения множества.
Пусть в нашем распоряжении имеется N цветов, занумерованных для определённости от 0 до N-1. Будем считать, опять же для определённости, что черный цвет имеет номер 0. Если для данного c после N-1 итераций точка не вышла за круг радиуса 2, будем считать, что c принадлежит множеству Мандельброта, и покрасим эту точку c в чёрный цвет. Иначе, если на некотором шаге k (k Є [1; N-1]) очередная точка вышла за круг радиуса 2 (т.е. на k-ом шаге мы поняли, что она "убегает"), покрасим её в цвет k.
Красивые изображения получаются при удачном выборе палитры и окрестности множества (а именно вне множества мы и получим "цветные точки). (Рис. 5, 6).

Рис. 4
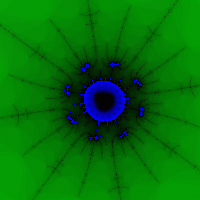

Рис. 5 Рис. 6
Основные понятия теории узлов
Модель узла - замкнутая, несамопересекающаяся кривая в пространстве.
Узел – это замкнутая линия в пространстве, гладкая или ломаная, которая может быть как угодно закручена и переплетена.
Под развязыванием узла будем понимать выпрямление этого отрезка путем деформации его в трехмерном пространстве.
тривиальный узел (окружность)
Изображение узла называется диаграммой узла.
Зацеплением называется конечный набор замкнутых непересекающихся ориентированных ломаных в пространстве.
Два узла называются изотопными (эквивалентными), если от одного к другому можно перейти последовательно выполняя преобразования, которые называются элементарными изотопиями.
Два узла изотопны, если один узел можно перевязать в другой, не разрезая его и не допуская самопересечений.
