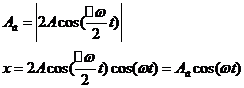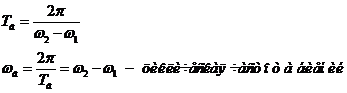Сложение однонаправленных колебаний. Векторные диаграммы. Биения.

Сложение однонаправленных колебаний. Векторные диаграммы. Биения.

В дальнейших расчётах результатов сложений колебаний нам помогут векторные диаграммы.

Векторная диаграмма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков - векторов. Гармоническое колебание может быть представлено графически в виде проекции на некоторую ось (обычно берут ось координат Оx) вектора, вращающегося с постоянной угловой скоростью ω. Длина вектора соответствует амплитуде, угол поворота относительно оси (Ox) - фазе.

Сумма (или разность) двух и более колебаний на векторной диаграмме представлена при этом геометрической суммой (или разностью) векторов этих колебаний. Мгновенное значение искомой величины определяется при этом проекцией вектора суммы на ось Оx, амплитуда - длиной этого вектора, а фаза - углом его поворота относительно Ox.

1) Сложение однонаправленных колебаний с одинаковыми частотами:

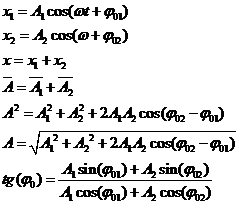Пусть система принимает участие в двух однонаправленных колебаниях с одной .

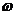Сколько бы гармонических колебаний ни складывалось, получаем гармоническое колебание с такой же частотой, но у него своя амплитуда, которая зависит от амплитуды складываемых колебаний и от начальных фаз.

Важные частные случаи:

1. 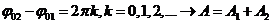- колебания происходят в одной фазе

2. 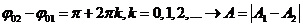- колебания называются противофазными

2) Сложение однонаправленных колебаний с разными частотами. Биения.

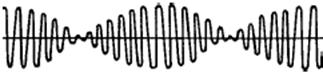
Для практики особый интерес представляет случай, когда два складываемых гар­монических колебания одинакового направления мало отличаются по частоте. В ре­зультате сложения этих колебаний получаются колебания с периодически изменяющей­ся амплитудой. Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называютсябиениями.

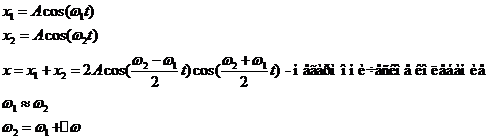
Результирующее колебание можно интерпретировать как быстрое колебание с медленно изменяющейся амплитудой.

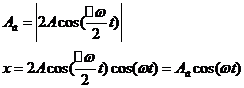
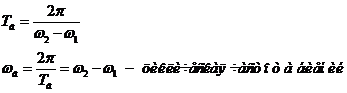
Затухающие колебания колебательного контура. Дифференциальное уравнение и его решение. Характеристики колебаний. Энергия колебаний. Добротность.

В реальных осцилляторах есть трение, трение трансформирует энергию колебаний во внутреннюю энергию. При достаточно большом трении колебаний может и не быть.

Гипотеза Эйнштейна

Свет не только излучается, но и поглощается в виде порций, квантов.

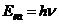- энергия кванта

Фотоны, падая на поверхность металла, поникают на очень короткое расстояние в металл и поглощаются нацело отдельными его электронами проводимости. Они сразу же увеличивают свою энергию до значения, достаточного, чтобы преодолеть потенциальный барьер вблизи поверхности металла, и вылетают наружу.

Закон сохранения энергии позволяет написать простое соотношение, связывающее скорость фотоэлектронов с частотой поглощаемого света.

Энергия фотона после поглощения его, с одной стороны, расходуется на преодоление потенциального барьера (эта часть энергии называется работой выхода электрона из металла), а с другой стороны, частично сохраняется у электрона вне металла в виде кинетической энергии. Таким образом, соотношение для энергии таково: , где А - работа выхода электрона. Это соотношение подтверждает тот факт, что энергия фотоэлектронов, действительно, никак не зависит от интенсивности света, а линейно зависит от частоты света.

1. 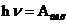если меньше, то только нагрев

2. Кинетическая энергия вылетевших электронов .

т.к. свет излучается и поглощается квантами, то световой поток это всегда поток

квантов (локализованных порций) – фотонов.

Свойства потока (они есть у фотона)

1.

2. импульс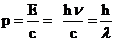

3. mo=0 если фотон останавливается то он исчезает.

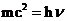- релятивистская масса фотона.

Три закона внешнего фотоэффекта:

1.Число фотоэлектронов n, вырываемых из катода за единицу времени, пропорционально интенсивности света.

2. Максимальная начальная скорость фотоэлектронов определяется частотой света и не зависит от его интенсивности.

3. Для каждого вещества существует “красная граница” фотоэффекта, те min частота света, при которой еще возможен фотоэффект. Она зависит от химической природы вещества и состояния его поверхности.

Образование молекул. Ковалентная и ионная связь.

Молекулярные структуры существуют благодаря химическим связям, которые обеспечиваются электронами валентных оболочек.

Связи образуются за счёт частичной или полной передачи валентных электронов.

1. Ковалентная связь

Обусловлена обменом парой электронов с противоположным спином.

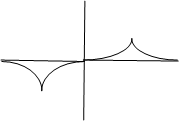
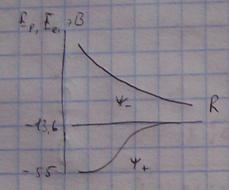
Начинаем сближать эти две ямы. Электрон может попадать из одной ямы в другую. В конце концов он перестанет различать эти две ямы и будет принадлежать двум ямам.

ψ₁₂=ψ₁±ψ₂

ψ₊=ψ₁+ψ₂

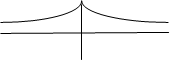
ψ_-=ψ₁-ψ₂

	ψ+

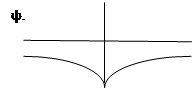
Симметричная функция

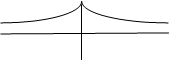Состояние, стягивающее систему.

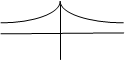
Антисимметричная функция

Состояние, разваливающее систему.

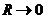
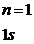
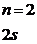
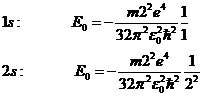
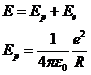
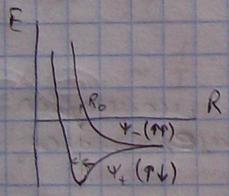F=grad(v)

( ) – направление спинов

Состояние ψ₊ характеризуется minэнергии и является связывающим.

Молекула водорода образуется только в случае, если 2 электрона направлены с разнонаправленными спинами. В противном случае молекула не образуется.

Ковалентная связь является обменным взаимодействием.

Ионная связь.

Для ионной связи характерна полная передача электронов одного атома другому.

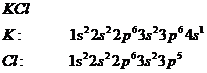
По мере объединения атомов молекулы исходного атомарного уровня расщепляются.

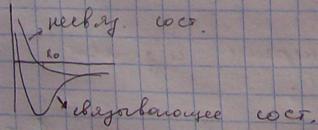
По мере сближения атомов снимается (?) вырождение состояний

Сложение однонаправленных колебаний. Векторные диаграммы. Биения.

В дальнейших расчётах результатов сложений колебаний нам помогут векторные диаграммы.

Векторная диаграмма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков - векторов. Гармоническое колебание может быть представлено графически в виде проекции на некоторую ось (обычно берут ось координат Оx) вектора, вращающегося с постоянной угловой скоростью ω. Длина вектора соответствует амплитуде, угол поворота относительно оси (Ox) - фазе.

Сумма (или разность) двух и более колебаний на векторной диаграмме представлена при этом геометрической суммой (или разностью) векторов этих колебаний. Мгновенное значение искомой величины определяется при этом проекцией вектора суммы на ось Оx, амплитуда - длиной этого вектора, а фаза - углом его поворота относительно Ox.

1) Сложение однонаправленных колебаний с одинаковыми частотами:

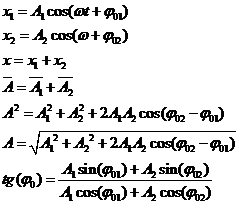Пусть система принимает участие в двух однонаправленных колебаниях с одной .

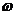Сколько бы гармонических колебаний ни складывалось, получаем гармоническое колебание с такой же частотой, но у него своя амплитуда, которая зависит от амплитуды складываемых колебаний и от начальных фаз.

Важные частные случаи:

1. 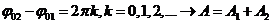- колебания происходят в одной фазе

2. 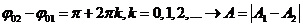- колебания называются противофазными

2) Сложение однонаправленных колебаний с разными частотами. Биения.

Для практики особый интерес представляет случай, когда два складываемых гар­монических колебания одинакового направления мало отличаются по частоте. В ре­зультате сложения этих колебаний получаются колебания с периодически изменяющей­ся амплитудой. Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называютсябиениями.

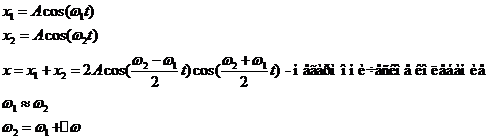
Результирующее колебание можно интерпретировать как быстрое колебание с медленно изменяющейся амплитудой.