Выражения, тождества, уравнения

Основная цель — систематизировать и обобщить сведения

о преобразованиях алгебраических выражений и решений урав-нений с одной переменной.

В соответствии с требованием федерального компонента госу-дарственного образовательного стандарта основного общего об-разования по математике первую тему 7 класса следует рассматри-вать как «связующее звено» между курсом математики 5–6 классов и курсом алгебры.

На уроках вводного повторения рекомендуется проводить в устной работе многократное повторение правил действий с раци-ональными числами. Нахождение значений числовых и буквенных выражений дает возможность закрепить вычислительные навыкис рациональными числами, а в случае необходимости (после не-больших проверочных работ) организовать тренировочные заня-тия, карточки с домашними заданиями для ликвидации выявлен-

ных пробелов. Уделяя развитию навыков вычисления серьезное внимание, систематически проводим устные разминки-вычисле-ния, комментирование с места.

При рассмотрении преобразований выражений повторяем из-

ученные ранее свойства действий над числами, подчеркивая, что

они составляют основу тождественных преобразований. Правила вывешиваются на дополнительную доску, сопровождая работу по теме как опорный сигнал.

Теоретические сведения при изучении темы «Уравнения с од-ной переменной», такие как «равносильность уравнений», фор-мулируются и разъясняются на конкретных примерах. Уровень сложности при изучении линейных уравнений остается таким же, как и в 6 классе. Однако, помогая учащимся проводить исследо-вание решения уравнения вида ax = b при различных значениях

а и b, средства алгебры способствуют развитию аналитического мышления.

Важная тема «Решение задач с помощью уравнений» остается трудной для большинства учащихся. Многие дети плохо читают,

и если навыки смыслового чтения не сформированы в достаточ-ной степени, то учителю предстоит добиваться коррекции умений учащихся на своих уроках. Многократное прочтение текста зада-чи, подводящий диалог о данных, подбор интересных по содержа-нию задач, особенно практического направления — всё это помо-гает осмыслить задачу и составить её математическую модель, то есть уравнение. В 7 классе продолжается работа по формированию у учащихся умения использовать аппарат уравнений как средство для решения задач. Такая работа, кроме того, способствует фор-мированию и коррекции еще одной из важных способностей уча-щихся — развитию речи.

Решить как можно больше задач на уроке возможно путем фронтальной работы с классом, иногда ограничивая работу толь-ко составлением уравнения, не решая его. Работа в группах помо-жет разделить этапы решения задач.

Ознакомление учащихся в 7 классе с простейшими статисти-ческими характеристиками:средним арифметическим,модой,ме-дианой, размахом, а также способами организации статистиче-ских исследований — в 8 классе носит обзорный характер и имеет цель сформировать представление о статистике как особом на-правлении в математике.

В 8 классе тема «Выражения» продолжается в изучении раци-ональных дробей. Максимально сокращая сложность выражений,необходимо уделять особое внимание отработке умений выпол-нять сложение, вычитание, умножение и деление дробей, так как они являются опорными преобразованиями дробных выражений.

Функции

Одно из основных понятий в математике сквозной линией на-

чинается в 7 классе (линейная функция y = kx + b) и развивается

в старших классах (C= ^k_x , y = x² , y = x³, y = x — в 8 классе). Форми-рование всех функциональных понятий и выработка соответству-

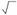
ющих навыков, а также изучение конкретных функций сопрово-ждаются рассмотрением примеров реальных зависимостей между величинами, что облегчает усвоение учебного материала для уча-щихся, устанавливает межпредметные связи, способствует усиле-нию прикладной направленности курса алгебры.

Степень

При изучении этой темы (в 7 классе — степень с натуральным показателем, а в 8 — степень с целым показателем) способствуем выработке умения выполнять действия над степенями и приме-нять свойства степени в вычислениях и преобразованиях выраже-ний. Этому помогают многократное повторение и проговаривание правил действий, опорные сигналы в виде формул, отражающие свойства степени. При выполнении заданий на нахождение зна-чений выражений, содержащих степени, особое внимание следует обратить на порядок действий.