Транзитивное замыкание нечетких отношений
Большое значение в приложениях теории нечетких отношений играют транзитивные отношения. Они обладают многими удобными свойствами и определяют некоторую правильную структуру множества  . Например, если отношение
. Например, если отношение 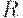 в
в  характеризует сходство между объектами, то транзитивность такого отношения обеспечивает возможность разбиения множества
характеризует сходство между объектами, то транзитивность такого отношения обеспечивает возможность разбиения множества  на непересекающиеся классы сходства. Если же отношению в
на непересекающиеся классы сходства. Если же отношению в  придать смысл "предпочтения" или "доминирования", тотранзитивность такого отношения обеспечивает возможность естественного упорядочения объектов множества
придать смысл "предпочтения" или "доминирования", тотранзитивность такого отношения обеспечивает возможность естественного упорядочения объектов множества  , существование "наилучших", "недоминируемых" объектов и т.п. Поэтому представляет большой интерес возможность преобразования исходного нетранзитивного отношения в транзитивное. Такое преобразование обеспечивает операциятранзитивного замыкания нечеткого отношения.
, существование "наилучших", "недоминируемых" объектов и т.п. Поэтому представляет большой интерес возможность преобразования исходного нетранзитивного отношения в транзитивное. Такое преобразование обеспечивает операциятранзитивного замыкания нечеткого отношения.
Транзитивным замыканием отношения 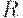 называется отношение
называется отношение 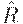 , определяемое следующим образом:
, определяемое следующим образом:
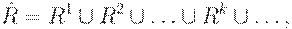
где отношения 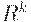 определяются рекурсивно:
определяются рекурсивно:
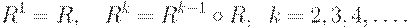
Теорема. Транзитивное замыкание 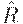 любого нечеткого отношения
любого нечеткого отношения 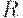 транзитивно и является наименьшим транзитивным отношением, включающим
транзитивно и является наименьшим транзитивным отношением, включающим 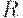 , т.е.
, т.е. 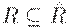 , и для любого транзитивного отношения
, и для любого транзитивного отношения 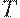 , такого, что
, такого, что 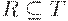 , следует
, следует 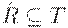 .
.
Как следствие из данной теоремы получаем, что 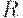 транзитивно тогда и только тогда, если
транзитивно тогда и только тогда, если 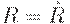 .
.
Если множество  содержит
содержит 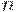 элементов, то имеем
элементов, то имеем
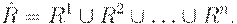
В случае, когда 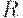 рефлексивно, имеем
рефлексивно, имеем
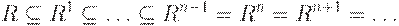
Весьма полезным фактором является то, что 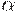 -уровень транзитивного замыкания нечеткого отношения
-уровень транзитивного замыкания нечеткого отношения 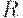 совпадает странзитивным замыканием соответствующего
совпадает странзитивным замыканием соответствующего 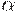 -уровня:
-уровня:
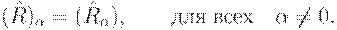
Заметим, что при транзитивном замыкании нечеткого отношения 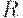 в общем случае сохраняются лишь некоторые свойства отношения
в общем случае сохраняются лишь некоторые свойства отношения 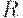 . Такими свойствами являются рефлексивность, симметричность, линейность и транзитивность.
. Такими свойствами являются рефлексивность, симметричность, линейность и транзитивность.
Проекции нечетких отношений
Важную роль в теории нечетких множеств играет понятие проекции нечеткого отношения. Дадим определение проекции бинарного нечеткого отношения.
Пусть 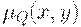 — функция принадлежности нечеткого отношения в
— функция принадлежности нечеткого отношения в 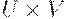 . Проекции
. Проекции 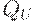 и
и 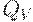 отношения
отношения 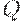 на
на 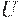 и
и 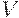 — есть множества в
— есть множества в 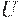 и
и 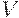 с функцией принадлежности вида
с функцией принадлежности вида
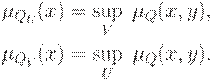
Условной проекцией нечеткого отношения 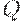 на
на 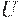 , при произвольном фиксированном
, при произвольном фиксированном  , называется множество
, называется множество 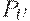 с функцией принадлежности вида
с функцией принадлежности вида  .
.
Аналогично определяется условная проекция на 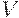 при заданном
при заданном 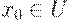 :
:

Из данного определения видно, что проекции 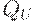 и
и 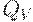 не влияют на условные проекции
не влияют на условные проекции 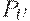 и
и 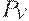 , соответственно. Дадим далее определение, которое учитывает их взаимосвязь.
, соответственно. Дадим далее определение, которое учитывает их взаимосвязь.
Условные проекции второго типа определяются следующим образом:
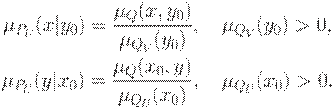
Если 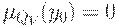 или
или 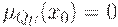 , то полагаем, соответственно, что
, то полагаем, соответственно, что 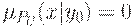 или
или 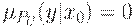 .
.
Заметим, что условные проекции первого типа содержатся в соответствующих проекциях второго типа.
Пусть 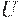 и
и 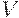 — базовые множества,
— базовые множества, 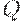 — нечеткое отношение в
— нечеткое отношение в 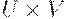 и
и 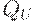 и
и 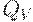 — его проекции на
— его проекции на 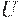 и
и 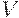 , соответственно.
, соответственно.
Нечеткие множества 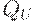 и
и 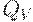 называются независимыми, если
называются независимыми, если
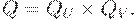
Следовательно, они независимы по первому типу, если
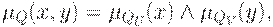
и независимы по второму типу, если
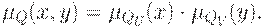
В противном случае проекции 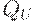 и
и 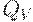 являются зависимыми (соответствующего типа).
являются зависимыми (соответствующего типа).
Независимость второго типа можно интерпретировать следующим образом. Данные соотношения с учетом произвольности 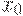 и
и 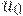 перепишем в виде
перепишем в виде
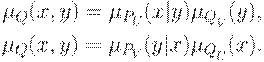
Классы нечетких отношений
Аннотация: В лекции приводится классификация нечетких отношений, рассматриваются классы нечетких отношений сходства и различия, а также класс нечетких порядков. В качестве примеров применения теории нечетких отношений рассматриваются задачи нечеткой классификации и нечеткого упорядочения.
Все типы нечетких отношений в зависимости от свойств, которыми они обладают, могут быть разделены на три больших класса.
В первый класс входят симметричные отношения, которые обычно характеризуют сходство или различие между объектами множества  .
.
Второй класс образуют антисимметричные отношения; они задают на множестве  отношения упорядоченности, доминирования, подчиненности и т.п.
отношения упорядоченности, доминирования, подчиненности и т.п.
Третий класс состоит из всех остальных отношений.
Отношения каждого класса, в свою очередь, могут быть разделены на подклассы в зависимости от выполнения условий рефлексивности и антирефлексивности.
Рефлексивные и симметричные отношения обычно называют отношениями сходства, толерантности, безразличия или неразличимости. В дальнейшем эти отношения будем называть отношениями сходства и обозначать буквой 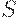 .
.
Антирефлексивные и симметричные отношения называютсяотношениями различияи обозначаются буквой 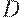 .
.
Отношения сходства и отношения различиядвойственны друг другу.
Антисимметричные отношения, называемые предпорядками и обозначаемые буквой 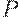 , в зависимости от выполнения условия рефлексивности или антирефлексивности делятся на нестрогие и строгие порядки.
, в зависимости от выполнения условия рефлексивности или антирефлексивности делятся на нестрогие и строгие порядки.
Из отношений третьего класса, обозначаемых буквой 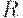 , обычно выделяют лишь рефлексивные отношения, которые будут называться слабыми порядками.
, обычно выделяют лишь рефлексивные отношения, которые будут называться слабыми порядками.
На следующем уровне классификации из каждого класса отношений могут быть выделены отношения специального вида. Определяющим условием для них является условие транзитивности. Оно устанавливает связь между силой отношения для различных пар объектов из  .
.
Эта связь может быть очень слабой, а может накладывать достаточно сильные ограничения на возможные значения силы отношения между объектами из  . Число отличающихся друг от друга условий транзитивности зависит от типа отношения, для которого они формулируются.
. Число отличающихся друг от друга условий транзитивности зависит от типа отношения, для которого они формулируются.
Условия транзитивности зависят от вида операций, с помощью которых они определяются. Наиболее общими условиями транзитивности являются условия, определяемые с помощью решеточных операций 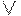 и
и 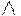 в
в  . Более частыми являются условия, определяемые с помощью дополнительных операций в
. Более частыми являются условия, определяемые с помощью дополнительных операций в  и зависящих от конкретного вида
и зависящих от конкретного вида  . В этих случаях указывается вид соответствующего множества
. В этих случаях указывается вид соответствующего множества  . Далее мы будем рассматривать нечеткие отношения, определенные на множестве
. Далее мы будем рассматривать нечеткие отношения, определенные на множестве 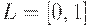 .
.
