О методах построения функций принадлежности нечетких множеств

В приведенных выше примерах использованы прямые методы, когда эксперт либо просто задает для каждого х ϵ Езначение μ_А(х),либо определяет функцию совместимости. Как правило, прямые методы задания функции принадлежности ис­пользуются для измеримых понятий, таких как скорость, время, расстояние, давление, температура и т.д., или когда выделяются полярные значения.

Во многих задачах при характеристике объекта можно выде­лить набор признаков и для каждого из них определить полярные значения, соответствующие значениям функции принадлежности, 0 или 1.

Например, в задаче распознавания лиц можно выделить шкалы, приведенные в табл. 1.1.

Таблица 1.1. Шкалы в задаче распознавания лиц

x1	высота лба	низкий	высокий
x2	профиль носа	курносый	горбатый
x3	длина носа	короткий	длинный
x4	разрез глаз	узкие	широкие
x5	цвет глаз	светлые	темные
x6	форма подбородка	остроконечный	квадратный
x7	толщина губ	тонкие	толстые
x8	цвет лица	темный	светлый
x9	очертание лица	овальное	квадратное

Для конкретного лица А эксперт, исходя из приведенной шкалы, задает μA(х) ϵ [0, 1], формируя векторную функцию принад­лежности { μA(х1), μA(х2),…, μA(х9) }.

При прямых методах используются также групповые прямые методы, когда, например, группе экспертов предъявляют конкрет­ное лицо и каждый должен дать один из двух ответов: «этот че­ловек лысый» или «этот человек не лысый», тогда количество утвердительных ответов, деленное на общее число экспертов, дает значение μлысый (данного лица). (В этом примере можно действо­вать через функцию совместимости, но тогда придется считать число волосинок на голове у каждого из предъявленных эксперту лиц.)

Косвенные методы определения значений функции принадлежности используются в случаях, когда нет элементарных из­меримых свойств, через которые определяется интересующее нас нечеткое множество. Как правило, это методы попарных сравне­ний. Если бы значения функций принадлежности были нам из­вестны, например, μA(х­i) = ωi, i= 1, 2, ..., n,то попарные срав­нения можно представить матрицей отношений А = { aij}, где aij= ωi/ωj (операция деления).

На практике эксперт сам формирует матрицу А, при этом пред­полагается, что диагональные элементы равны 1, а для элемен­тов симметричных относительно диагонали aij= 1/aij, т.е. если один элемент оценивается в α раз сильнее, чем другой, то этот по­следний должен быть в 1/α раз сильнее, чем первый. В общем случае задача сводится к поиску вектора ω, удовлетворяющего уравнению вида Aw= λmaxw, где λmax— наибольшее собствен­ное значение матрицы А. Поскольку матрица А положительна по построению, решение данной задачи существует и является поло­жительным.

Можно отметить еще два подхода:

· использование типовых форм кривых для задания функций принадлежности (в форме (L-R)-Типа – см. ниже) с уточнением их параметров в соответствии с данными эксперимента;

· использование относительных частот по данным эксперимента в качестве значений принадлежности.

Операции над нечеткими множествами

Логические операции

Включение.Пусть А и В — нечеткие множества на универсальном множестве Е. Говорят, что А содержится в В, если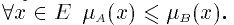

Обозначение: А⊂ В.

Иногда используют термин доминирование, т.е. в случае, ко­гда А⊂ В,говорят, что В доминирует А.

Равенство.А и В равны, если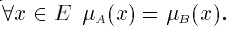

Обозначение: А = В.

Дополнение.Пусть М = [0, 1], А и В – нечеткие множества, заданные на Е. А и В дополняют друг друга, если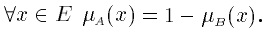

Обозначение: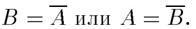

Очевидно, что 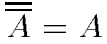(дополнение определено для М = [0, 1], но очевидно, что его можно определить для любого упорядоченногоМ).

Пересечение. А ⋂ В— наибольшее нечеткое подмножество, содержащееся одновременно в Аи В:

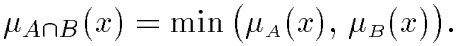
Объединение.A∪В — наименьшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности:

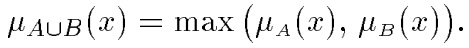
Разность. 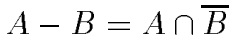с функцией принадлежности:

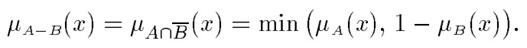
Дизъюнктивная сумма

А⊕ В = (A - B) ∪ (B - A) = (A ⋂ ̅B) ∪ ( ̅A ⋂ B)

с функцией принадлежности:

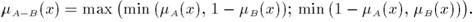
Примеры.Пусть

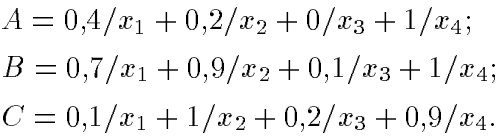
Здесь:

1) А ⊂ В, т. е. А содержится в B или Bдоминирует А С несравнимони с A, ни с В, т.е. пары {А, С} и {А, С} — пары недоминируемых нечетких множеств.

2) A≠ B ≠ C

3) ̅A = 0,6/x₁ + 0,8/x₂ + 1/x₃ + 0/x₄; ̅B = 0,3/x₁ + 0,1/x₂ + 0,9/x₃ +0/x₄.

4) А ⋂ В = 0,4/x₁+ 0,2/x₂+ 0/x₃+ 1/х₄.

5) A ∪ В = 0,7/x₁+ 0,9/x₂+ 0,1/x₃+ 1/x₄.

6) А - В = А⋂ ̅В =0,3/x₁+ 0,l/x₂+ 0/x₃+ 0/x₄;

В- А= ̅А⋂ В=0,6/x₁+ 0,8/x₂+ 0,l/x₃+ 0/x₄.

7) А ⊕ В = 0,6/x₁+ 0,8/x₂+ 0,1/x₃+ 0/x₄.

Наглядное представление логических операций над нечеткими множествами. Для нечетких множеств можно строить визуальное представление. Рассмотрим прямоуголь­ную систему координат, на оси ординат которой откладываются значения μ_А(х), на оси абсцисс в произвольном порядке распо­ложены элементы Е (мы уже использовали такое представление в примерах нечетких множеств). Если Е по своей природе упо­рядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс. Такое представление делает нагляд­ными простые логические операции над нечеткими множествами (см. рис. 1.3).

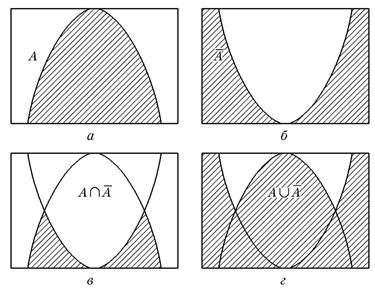
Рис. 1.3. Графическая интерпретация логических операций:
α— нечеткое множество А; б — нечеткое множество̅А, в — А⋂ ̅А; г—A ∪ ̅А

На рис. 1.3α заштрихованная часть соответствует нечеткому множеству А и, если говорить точно, изображает область значений А и всех нечетких множеств, содержащихся в А. На рис. 1.3б, в, гданы ̅А, А ⋂ ̅A,A U ̅А.

Свойства операций∪ и⋂

Пусть А, В, С — нечеткие множества, тогда выполняются сле­дующие свойства:

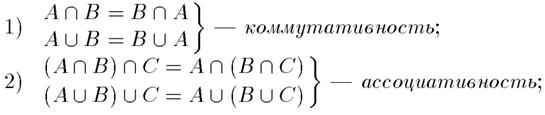
В отличие от четких множеств, для нечетких множеств в общем

случае:

A⋂̅A ≠∅, A ∪ ̅A ≠ E

(что, в частности, проиллюстрировано выше в примере наглядного представления нечетких множеств).

Замечание. Введенные выше операции над нечеткими мно­жествами основаны на использовании операций maxи min. В те­ории нечетких множеств разрабатываются вопросы построения обобщенных, параметризованных операторов пересечения, объеди­нения и дополнения, позволяющих учесть разнообразные смысло­вые оттенки соответствующих им связок «и», «или», «не».

Треугольные нормы и конормы

Один из подходов к операторам пересечения и объединения за­ключается в их определении в классе треугольных норм и конорм.

Треугольной нормой(t-нормой) называется бинарная операция (двуместная действительная функция)

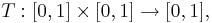
удовлетворяющая следующим условиям:

1. Ограниченность: .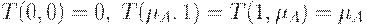

2. Монотонность: .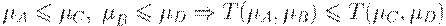

3. Коммутативность: .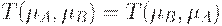

4. Ассоциативность: .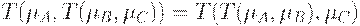

Примеры треугольных норм

min(μ_A,μ_B)

произведение μ_A·μ_B

max(0, μ_A+μ_B - 1).

Треугольной конормой (сокращенно 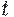-конормой) называется двухместная действительная функция

,

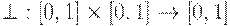удовлетворяющая следующим условиям:

1. Ограниченность: .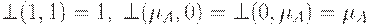

2. Монотонность: .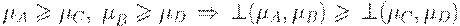

3. Коммутативность: .

4. Ассоциативность: .

Треугольная конорма 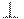является архимедовой, если она непрерывна
и для любого нечеткого множества 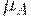выполнено неравенство .

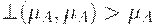Она называется строгой, если функция 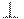строго убывает по обоим аргументам.

Примеры t-конорм

max(μ_A,μ_B)

μ_A+μ_B-μ_A·μ_B

min(1, μ_A+μ_B).

Примерами треугольных конорм являются следующие операторы:

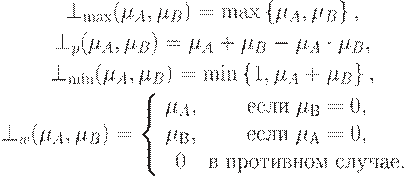
Треугольная норма T и треугольная конорма S называются дополнительными бинарными операциями, если

T(a,b) + S(1 − a,1 − b) = 1

для .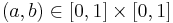

Наибольшей популярностью в теории Заде пользуются три пары дополнительных треугольных норм и конорм.

1) Пересечение и объединение по Заде:

T_Z(a,b) = min{a,b}, S_Z(a,b) = max{a,b}.

2) Пересечение и объединение по Лукасевичу:

.

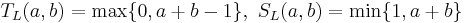3) Вероятностное пересечение и объединение:

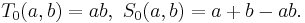
Операторы дополнения

В теории нечетких множеств оператор дополнения не является единственным.

Помимо общеизвестного

,

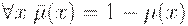существует целый набор операторов дополнения нечеткого множества.

Пусть задано некоторое отображение

.

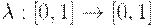Это отображение будет называться оператором отрицания в теории нечетких множеств, если выполняются следующие условия:

(1)

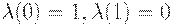
(2)

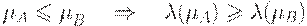
Если кроме этого выполняются условия:

(3) 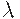— строго убывающая функция

(4) — непрерывная функция

то она называется строгим отрицанием.

Функция 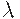называется сильным отрицанием или инволюцией, если наряду с условиями (1) и (2) для нее справедливо:

(5) .

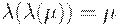Приведем примеры функции отрицания:

Классическое отрицание: .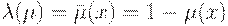

Квадратичное отрицание: .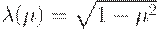

Отрицание Сугено: .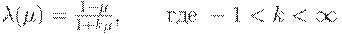

Дополнение порогового типа: .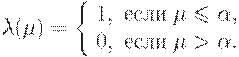

Будем называть любое значение 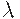, для которого 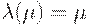, равновесной точкой. Для любого непрерывного отрицания существует единственная равновесная точка.