Нахождение производных функций

Таблица производных:
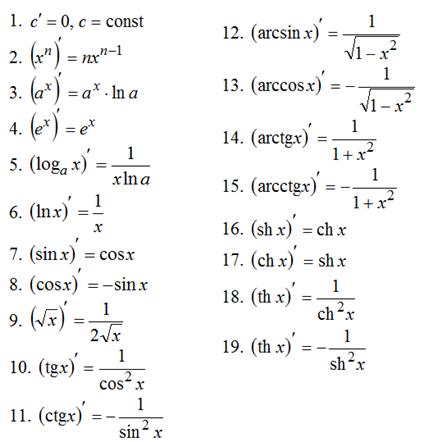
Таблица производных сложных функций
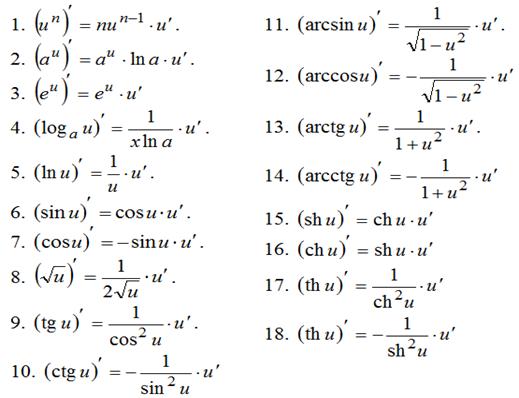
| Задание 1. | Найти производную функции 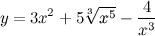 |
| Решение. | Для нахождения производной данной функции используем правила дифференцирования и таблицу производных. Так как производная суммы/разности равна сумме/разности производных, то 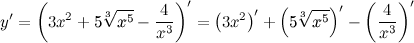 постоянный множитель можно вынести за знак производной постоянный множитель можно вынести за знак производной 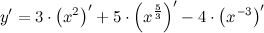 Воспользуемся формулой для производной степенной функции: Воспользуемся формулой для производной степенной функции: 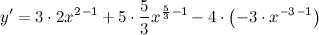 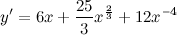 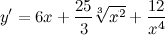 |
| Ответ. | 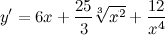 |
| Задание 2. | Найти производную функции 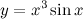 |
| Решение. | По правилу дифференцирования произведения получаем: 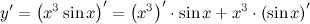 теперь воспользуемся формулами для производных степенной и тригонометрической функций: теперь воспользуемся формулами для производных степенной и тригонометрической функций: 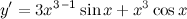 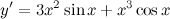 |
| Ответ. | 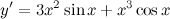 |
| Задание 3. | Найти производную функции 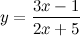 |
| Решение. | Воспользуемся правилом дифференцирования частного: 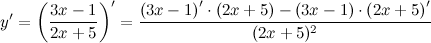 Производная суммы/разности равна сумме/разности производных и константу можно выносить за знак производной, поэтому имеем: Производная суммы/разности равна сумме/разности производных и константу можно выносить за знак производной, поэтому имеем: 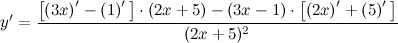 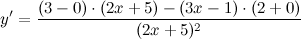 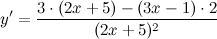 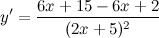 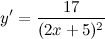 |
| Ответ. | 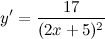 |
| Задание 4. | Найти производную функции 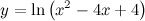 |
| Решение. | По свойству дифференцирования сложной функции вначале находим производную натурального логарифма и домножаем на производную подлогарифмической функции: 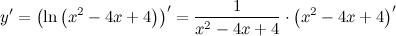 Производная суммы равна сумме производных и константу можно выносить за знак производной, поэтому имеем: Производная суммы равна сумме производных и константу можно выносить за знак производной, поэтому имеем: 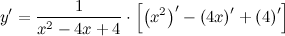 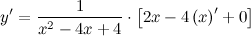 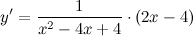 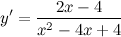 Знаменатель дроби можно свернуть по формуле квадрат разности, а в числителе двойку вынесем как общий множитель за скобки: Знаменатель дроби можно свернуть по формуле квадрат разности, а в числителе двойку вынесем как общий множитель за скобки: 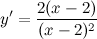 сокращаем: сокращаем: 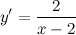 |
| Ответ. | 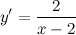 |
| Задание 5. | Найти производную функции 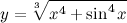 |
| Решение. | По свойству дифференцирования сложной функции и используя формулы вычисления производной показательной и тригонометрических функций, получим: 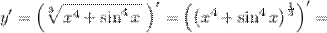 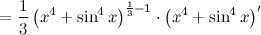 Производная суммы равна сумме производных: Производная суммы равна сумме производных: 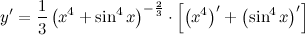 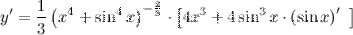 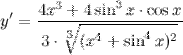 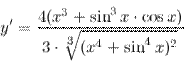 Для вычисления данной производной использовались правила дифференцирования и таблица производных сложных функций. Для вычисления данной производной использовались правила дифференцирования и таблица производных сложных функций. |
| Ответ. | 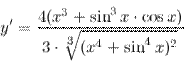 |
| Задание 6. | Найти производную функции 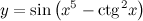 |
| Решение. | По правилу дифференцирования сложной функции: 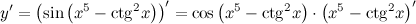 По правилу дифференцирования разности: По правилу дифференцирования разности: 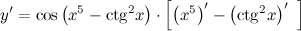 Производная Производная 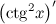 берется по правилу дифференцирования сложной функции: берется по правилу дифференцирования сложной функции: 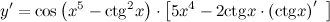 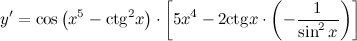 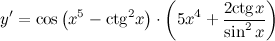 Для решения данной производной мы воспользовались правилами дифференцирования и таблицей производных сложных функций. Для решения данной производной мы воспользовались правилами дифференцирования и таблицей производных сложных функций. |
| Ответ. | 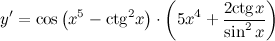 |
| Задание 7. | Найти производную функции 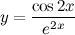 |
| Решение. | Сначала воспользуемся правилом дифференцирования частного: 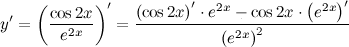 Затем каждую производную вычислим по правилу дифференцирования сложной функции: Затем каждую производную вычислим по правилу дифференцирования сложной функции: 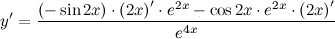 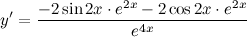 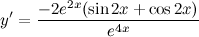 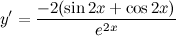 Таблица производных сложных функций - ссылка. Таблица производных сложных функций - ссылка. |
| Ответ. | 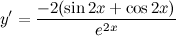 |
| Задание 8. | Найти производную функции 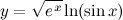 |
| Решение. | Перепишем исходную функцию в виде 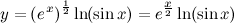 По правилу дифференцирования произведения имеем: По правилу дифференцирования произведения имеем: 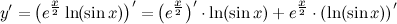 Затем находим производную по правилу дифференцирования сложной функции имеем: Затем находим производную по правилу дифференцирования сложной функции имеем: 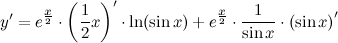 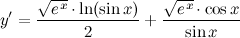 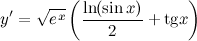 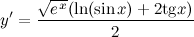 |
| Ответ. | 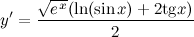 |
Интегрирование
Неопределённый интеграл и непосредственное интегрирование
Непосредственное интегрирование – это нахождение неопределенных интегралов с использованием таблицы интегралов и свойств неопределенного интеграла:
1. 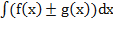 =
= 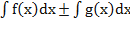
2. 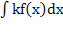 =k
=k 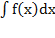 , где k=const
, где k=const
Таблица интегралов
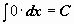 | 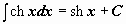 | ||
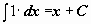 | 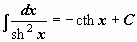 | ||
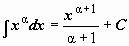 ( ( 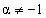 ) ) | 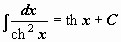 . . | ||
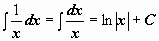 | 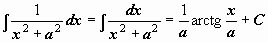 | ||
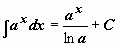 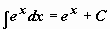 | 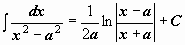 | ||
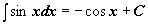 | 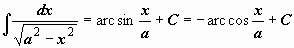 | ||
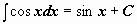 | 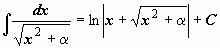 | ||
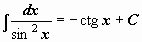 | 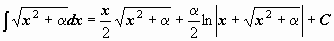 | ||
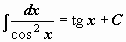 | 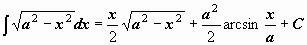 | ||
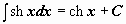 | 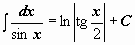 | ||
 |
