Уравнение Бернулли и закон сохранения импульса

Уравнение, полученное Даниилом Бернулли в 1738 году и носящее его имя, проще всего вывести из уравнения Эйлера, датированного 1757 годом. Для этого запишем уравнение (1.1) в форме Громэко - Лэмба:

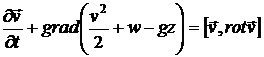, (3.1)

где 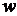- функция энтальпии, а направление оси 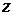совпадает с направлением вектора 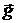. Рассмотрим частные случаи.

· Если движение стационарное 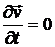и безвихревое (потенциальное) 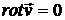, то

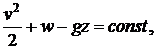(3.2)

причем постоянная сохраняется во всем потоке. Если при этом жидкость однородна и несжимаема, то получаем классическое уравнение, предложенное Д. Бернулли для описания стационарного потенциального движения однородной несжимаемой жидкости:

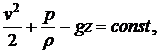(3.3)

· Если движение жидкости стационарное и вихревое 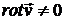, то

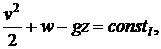(3.4)

при этом постоянная различна для разных линий тока. Напомним, что линией тока называют линию, касательная к которой в каждой точке совпадает по направлению с вектором скорости 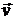в этой точке.

· Если движение нестационарное 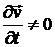и безвихревое 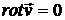, то

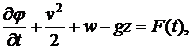(3.5)

где 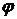- потенциал скорости 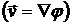, 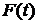- произвольная функция времени.

Для вывода закона сохранения импульса, рассмотрим импульс единицы объема 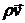и найдем производную по времени от его i-ой компоненты:

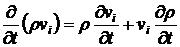. (3.6)

Из уравнения Эйлера (1.1) следует, что первое слагаемое уравнения (3.6) равно 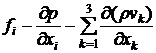, где - внешняя сила, действующая на единицу объема. Второе слагаемое в (3.6) несложно получить из уравнения неразрывности (1.2): 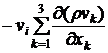. Вводя тензор плотности потока импульса 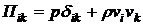, где 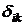- символ Кронекера, выражение (3.6) можно записать в следующем виде:

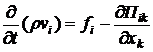, (3.7)

здесь по дважды встречающемуся индексу подразумевается суммирование. Теперь проинтегрируем равенство (3.7) по произвольному фиксированному объему V, ограниченному поверхностью S с внешней нормалью 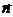, используя теорему Гаусса-Остроградского:

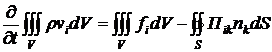. (3.8)

Таким образом, изменение импульса в объеме V связано с действием внешних объемных сил и потоком импульса через граничную поверхность S. В векторном виде выражение (3.8) можно представить следующим образом:

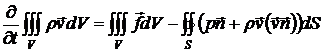. (3.9)

Если движение жидкости стационарно и отсутствуют массовые силы, то поток тензора плотности импульса через любую взятую в жидкости замкнутую поверхность равен нулю:

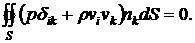(3.10)

Примеры решения задач

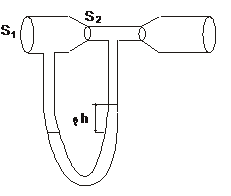1. Несжимаемая однородная жидкость плотности 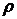движется по трубке переменного сечения (площади поперечных сечени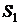й и 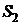известны). С трубкой соединен манометр U-образной формы, содержащий ртуть плотности 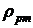(трубка Вентурра). Разность уровней ртути в манометре 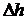. Определить скорость течения жидкости по трубе.

Решение: Обозначим 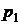, 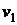соответственно давление и скорость жидкости в трубе с поперечным сечением 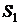, а в сечени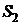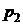и - и 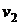(см. рисунок). Выберем линию тока из сечения 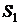в сечение 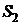, вдоль нее будет справедливо уравнение Бернулли:

.

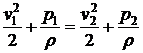Из закона сохранения массы жидкости, протекающей через поперечное сечение трубы в единицу времени следует, что

.

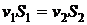Решая эти два уравнения относительно 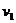, получаем:

.

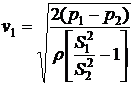Поскольку разность уровней ртути в манометре измеряет разность давлений 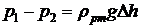, окончательно имеем:

.

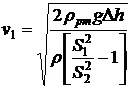2. Найти скорость 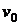истечения тяжелой несжимаемой жидкости из малого отверстия в стенке широкого сосуда. Считать, что давление на свободной поверхности и в струе жидкости на выходе из сосуда равно атмосферному - 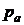, а площадь свободной поверхности 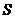много больше площади отверстия 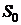. Уровень жидкости в сосуде относительно дна - , расстояние от отверстия до дна - (см. рисунок).

Решение: Выбираем линию тока, идущую от поверхности к отверстию. На поверхности и в струе непосредственно за отверстием давление одинаково - 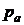, а скорость снижения уровня жидкости в сосуде пренебрежимо мала ( 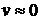), поскольку 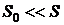. Направим ось 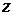вертикально вверх, т.е. против направления вектора ускорения свободного падения 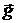. При таких условиях уравнение Бернулли принимает вид:

,

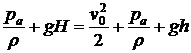откуда следует известная формула Торричелли

.

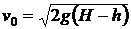Задачи для самостоятельного решения

3.1. Для стационарного течения жидкости показать, что уравнение Бернулли является следствием законов сохранения энергии и массы жидкости, протекающей по трубке тока.

3.2. Показать, что для равновесных обратимых изэнтропических процессов справедливо следующее соотношение: .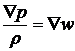

3.3. Чему равна скорость вытекающей из сосуда жидкости (см. условие предыдущей задачи), если учесть скорость снижения уровня воды в сосуде? Определить расстояние 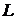, на котором вытекающая жидкость достигнет плоскости основания сосуда. При каком 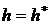это расстояние будет максимальным?

Ответ: ;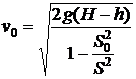

;

.

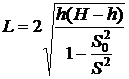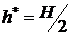3.4. Почему струя воды из крана сужается книзу?

3.5. Струя воды из крана сужается книзу. Выведите формулу для диаметра струи в зависимости от расстояния от крана. Начальная скорость вытекающей воды - 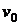, диаметр отверстия крана - .

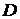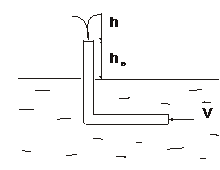
3.6. Изогнутую трубку опустили в поток воды как показано на рисунке. Скорость потока 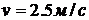. Закрытый верхний конец имеет небольшое отверстие и находится на высоте 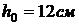. На какую высоту поднимется струя воды, вытекающая из отверстия?

Ответ: .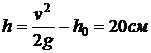

3.7. Чему равна подъемная сила крыла, обусловленная эффектом Бернулли, если площадь крыла равна 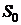, а скорости потока над крылом и под ним равны соответственно 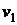и ?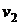

3.8. Чему рана скорость истечения газов из сопла ракеты? Плотность газа - 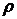, давление газа внутри ракеты - 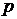, атмосферное давление - 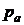. Площадь сопла 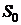много меньше площади поперечного сечения 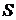камеры сгорания. Чему равна тяга двигателя, создаваемая выходящими из ракеты газами?

Ответ: ,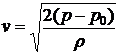

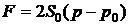
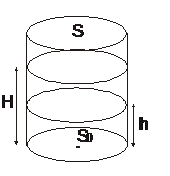3.9. В вертикально стоящий цилиндрический сосуд налита идеальная жидкость до уровня относительно дна сосуда. Площадь дна сосуда равна 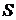. Определить время 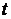, за которое уровень жидкости в сосуде опустится до высоты относительно дна сосуда, если в дне сосуда сделано малое отверстие площадью 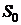. Определить также время 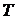, за которое из сосуда выльется вся жидкость.

Ответ: ;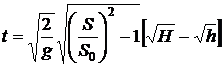

.

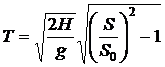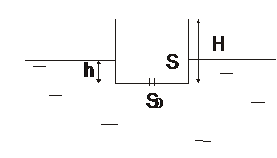3.10. Прямоугольная коробка плавает на поверхности воды, погружаясь под действием собственного веса на глубину . Площадь дна коробки равна 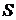, высота - . Через какое время коробка утонет, если в центре ее дна проделать малое отверстие площадью 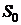и с помощью боковых направляющих сохранять неизменной ориентацию коробки?

Ответ: .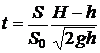

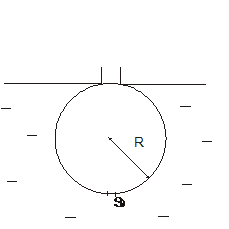
3.11. Через какое время наполнится водой шаровая колба радиусом 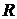, если в центре ее нижнего основания сделано малое отверстие площадью 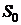? Колба погружена в воду до нижнего основания ее горлышка и жестко закреплена.

Ответ: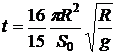

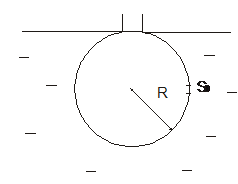
3.12. Через какое время наполнится водой шаровая колба радиусом 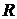, если в центре ее боковой поверхности сделано малое отверстие площадью 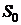? Колба погружена в воду до нижнего основания ее горлышка и жестко закреплена. Интересно сравнить результат с ответом предыдущей задачи.

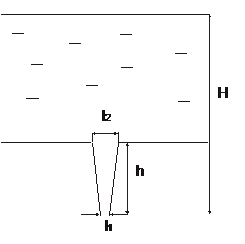3.13. В широкий сосуд с плоским дном налита идеальная жидкость. В дне сосуда сделана узкая и длинная щель, в которую вставлена насадка, образованная двумя плоскостями, наклоненными друг к другу под малым углом. Расстояние между ними в нижней части насадки равно 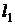, а в верхней - 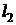. Определить распределение давления жидкости в насадке, если атмосферное давление равно 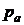, длина насадки - , расстояние между нижним концом насадки и уровнем жидкости - .

Ответ: .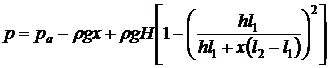

3.14. Вода вытекает из широкого резервуара через вертикальную коническую трубу, вставленную в его дно. Длина трубы 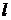, диаметр ее верхнего основания 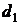, нижнего - 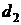, 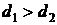. При каком уровне воды в резервуаре давление в верхнем сечении трубы будет равно 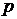, если атмосферное давление равно .

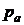Ответ: .

3.15. Определить 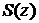- зависимость площади сечения сосуда от вертикальной координаты при условии, что скорость изменения уровня жидкости в сосуде 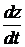при ее истечении через отверстие является постоянной. Коэффициент истечения жидкости через отверстие считать постоянным и равным 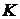. Площадь отверстия 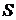. Высота отверстия над нулевым уровнем .

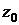Ответ: .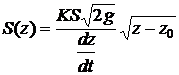

3.16. Определить форму сосуда, употребляемого для водяных часов (клепсидры). Скорость опускания уровня считать постоянной и равной 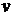. Площадь отверстия .

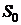Ответ: .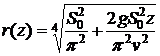

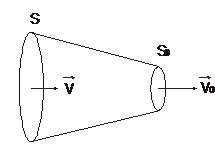3.17. При установившемся истечении газа из тонкой конической трубки траектории частиц представляют собой прямые, сходящиеся в вершине конуса. Предполагая, что движение совершается изотермически ( 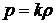), найти соотношение между скоростям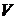и и 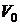в сечениях, площади которых 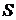и .

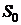Ответ: .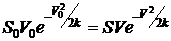

3.18. Показать, что при установившемся течении идеальной жидкости (газа) в тонкой трубке тока величина 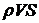во всех сечениях одинакова. Здесь 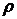- плотность, 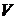- скорость, 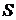- площадь поперечного сечения.

3.19. Газ (идеальная жидкость) плотности 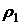, находящийся в сосуде под давлением 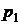, адиабатически вытекает через малое отверстие в стенке сосуда. Определить скорость истечения газа, если давление в окружающей среде равно 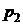, плотность - .

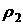Ответ: ,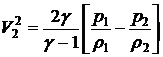

где 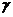- показатель адиабаты.

3.20. Выразить скорость истечения газа в предыдущей задаче через скорость звука в газе.

Ответ: .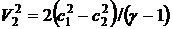

3.21. Найти массу газа, вытекающего в единицу времени 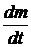через отверстие площадью 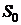в условиях задачи 3.21. Коэффициент истечения газа равен единице.

Ответ: .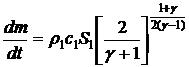

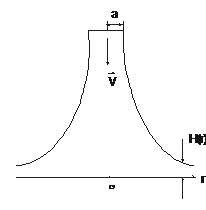3.22. На горизонтальную поверхность вертикально падает круглая струя радиуса 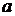со скоростью 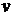. После падения струя растекается по горизонтальной плоскости. Пренебрегая влиянием силы тяжести, определить скорость растекания струи, толщину струи в зависимости от 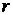и силу избыточного давления струи на стенку .

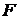Ответ: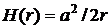

.

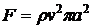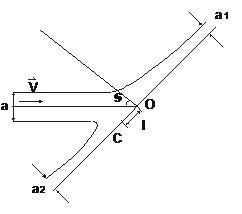3.23. Плоская струя воды ширины 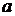, текущая со скоростью 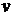, одинаковой для всех точек поперечного сечения, встречается под углом 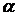с плоской бесконечной пластиной и разветвляется на две струи, линии тока которых по мере удаления от места разветвления асимптотически становятся параллельными пластине. Определить ширину этих стру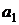й и 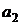на бесконечности, полную силу избыточного давления струи на стенку 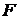и расстояние 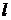от точки О пересечения пластинки с осью неразветвленной струи до центра давления С.

Ответ: , ,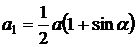

,

.

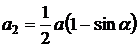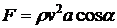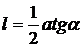3.24. Газ, находящийся в сосуде под давлением 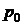, адиабатически вытекает через малое отверстие радиуса 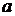в стенке сосуда. Давление в окружающей среде 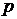, перемешивания с воздухом не происходит. Далее струя газа ударяется о плоскую стенку, расположенную перпендикулярно к струе, и растекается по ней. Найти силу избыточного давления струи на стенку.

Указание: воспользоваться решениями задач 3.21 и 3.24.

3.25. Идеальная однородная несжимаемая жидкость плотности 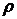вытекает из широкого резервуара через плоскую насадку. Ширина насадки 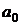, расположена она под углом 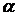к горизонту на высоте относительно земли. Уровень жидкости в резервуаре относительно земли. После удара о землю струя жидкости разветвляется на две струи, линии тока которых по мере удаления от места разветвления становятся горизонтальными. 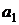Определить ширину струй и .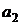

Указание: для нахождения скорости движения жидкости на разной высоте использовать уравнение Бернулли.

Контрольные вопросы

1. Закон сохранения импульса.

2. Тензор плотонсти потока импульса и его представление в декартовой системе координат.

3. Уравнение Бернулли для стационарного случая.

4. Уравнение Бернулли для нестационарного случая.