Точен ли первый закон кеплера?

Ответ на этот вопрос отрицательный. Как мы знаем, многие результаты, полученные в классической физике, после открытия теории относительности были скорректированы. Вблизи от Солнца пространство и время очень искривлены. В релятивистской интерпретации планеты следуют по прямолинейным траекториям в искривленном пространственно-временном континууме, и эта характеристика усиливается рядом с Солнцем. Именно из-за этого Меркурий стал планетой, данные о которой подверглись наибольшим уточнениям. Долгота его перигелия значительно увеличена по сравнению с классическим эллипсом.

Результатом всех уточнений стала открытая траектория – эллипс, не имеющий четкого перигелия. О смещении перигелия Меркурия, которое составляет 43” за 100 лет, было известно еще до Эйнштейна. Урбен Леверье, глава Парижской обсерватории, предсказавший существование Нептуна по возмущениям на орбите Урана, объяснял смещение перигелия Меркурия влиянием планеты, которая время от времени появляется на его орбите. Авторитет Леверье был высок, и довольно долго считалось, что такая планета, названная Вулканом, действительно существует. Ее открытие в течение нескольких десятилетий приписывалось астроному-любителю Эдмону Лескарбо (1814-1894).

Однако данные Лескарбо и других наблюдателей не согласовывались ни друг с другом, ни с расчетами Леверье, и существование планеты так и не удалось подтвердить. Лишь в начале XX века поведение Меркурия было объяснено с помощью общей теории относительности Эйнштейна без введения дополнительных небесных тел.

ЧЕРНАЯ ДЫРА В ЦЕНТРЕ МЛЕЧНОГО ПУТИ

Квазары – это далекие и мощные ядра галактик, в центре которых, как полагают, находится гигантская черная дыра массой порядка 1010 массы Солнца. Однако этот признак присущ не только квазарам. Считается, что в центре обычной галактики также есть черная дыра, хотя и не столь впечатляющего размера. Такая галактика, как Млечный Путь, может иметь черную дыру массой 106 массы Солнца.

МАССА ЧЕРНОЙ ДЫРЫ

Двадцать лет назад появились подробные изображения звезд, движущихся вокруг звезды Стрелец А*, компактного радиоисточника, находящегося в центре нашей галактики. Объектом изучения группы исследователей из Института внеземной физики Общества Макса Планка стала звезда S2. Первые результаты, опубликованные в 2003 году (группа Райнера Шёделя), подтвердили наличие у нее эллиптической орбиты. К такому же выводу пришла научная группа из Университета Лос- Анджелеса. Последние данные ученых из двух исследовательских центров (Стефан Гиллисен из Института внеземной физики, 2009 год, и Андреа Гез из Университета Лос-Анджелеса, 2008 год) позволили построить орбиту согласно первому закону Кеплера. Примерная масса черной дыры составила 4 300 000 масс Солнца.

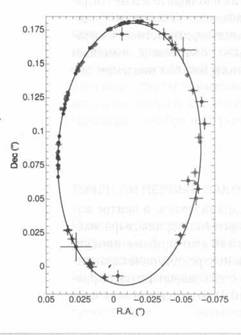
Орбита звезды S2 (в немецкой планетной номенклатуре), или S02 (в американской), пролегает в центре Млечного Пути вокруг черной дыры, равной 4,3-10 6 массы Солнца. Это изображение было опубликовано в The Astrophysical Journal. Особая благодарность Стефану Гиллисену из Американского физического общества.

Орбита звезды имеет очень высокий эксцентриситет, равный 0,87. Ее галактический перицентр составляет 17 световых лет, что в 3 раза превышает расстояние от Солнца до Плутона, а апоцентр – 10 световых лет. Максимальная скорость вращения равна 5000 км/сек, что в 200 раз превышает скорость вращения Земли вокруг Солнца.

Радиус Шварцшильда (гравитационный радиус) подобной черной дыры может составлять около 1010 м, в то время как радиус Солнца составляет порядка 7 108 м, то есть в черную дыру могут целиком уместиться некоторые звезды.

АККРЕЦИОННЫЙ ДИСК

Имеются все основания полагать, что черная дыра находится не только в центре Млечного Пути, но и в центре других галактик. Материя не поглощается ею сразу, а из-за эффекта сохранения кинетического момента скорость вращения по мере приближения к черной дыре растет – подобно тому, как вода все быстрее движется вокруг отверстия сливной трубы. Материя до поглощения черной дырой вращается вокруг нее, образуя аккреционный диск, который, предположительно, существует вокруг всех галактических черных дыр.

В аккреционном диске газ вращается вокруг черной дыры, расположенной в центре, однако, согласно третьему закону Кеплера, не все участки диска вращаются с одинаковой скоростью. Давайте мысленно разделим диск на тончайшие кольца. По третьему закону Кеплера, квадрат периода обращения этих колец пропорционален кубу расстояния до черной дыры, или же квадрат их угловой скорости w обратно пропорционален кубу расстояния r:

w²r³ = константа.

Угловая скорость колец неодинакова, слои, расположенные ближе к черной дыре, будут иметь большие скорости. Это обуславливает наличие внутреннего трения и нагревания, которые наиболее высоки по мере приближения к центру и ослабевают на внешних краях диска. Внутренние слои передают часть своего момента импульса наружу, при этом они приближаются к массивному центру и, в конце концов, падают на него. Фактически траектории отдельных частиц газа имеют вид спиралей, которые медленно закручиваются. Нагревание вследствие трения приводит к выбросу излучения, что и позволяет нам наблюдать черную дыру, вернее материю, которая вращается вокруг нее.

ЗВЕЗДНАЯ МАССА

Массу Солнца можно вычислить, наблюдая за любой планетой Солнечной системы и зная расстояние от нее до Солнца и период обращения планеты. Так же мы можем рассчитать массу Земли, зная расстояние от Земли до Луны и период обращения нашего спутника, – для этого необходимо всего лишь применить закон Кеплера в интерпретации Ньютона. При помощи этого же принципа и уже указанного закона Кеплера можно рассчитать звездную массу двойных звезд, и это вычисление является практически единственным непосредственным методом вычисления звездной массы. К счастью, частью двойной системы являются многие звезды, так что к настоящему времени наработана обширная статистическая база звездных масс. Масса звезды тесно связана с ее светимостью, или световым потоком, излучаемым в секунду времени. Соотношение массы и светимости имеет следующий вид:

L аМх ,

где L – светимость, М – масса, х – показатель степени, равный примерно 3 или чуть больше для звезд с очень большой массой.

Подобное соотношение справедливо не только для звезд, относящихся к звездам главной последовательности, которые состоят из идеального газа, 4Н -› Не.

Двойные звезды могут быть визуальными, спектральными и фотометрическими. В случае визуально-двойных звезд при длительном изучении, например в течение нескольких лет, можно наблюдать, как обе звезды вращаются вокруг общего центра масс, двигаясь при этом по эллиптической орбите. Спектрально-двойные и фотометрические двойные звезды обычно расположены настолько близко, что расчеты крайне затруднительны, так как мы можем наблюдать лишь одну звезду, хотя мы и знаем, что на самом деле их две. В этом случае периоды обращения, как правило, гораздо меньше, и их определение не требует много времени.

Спектрально-двойные звезды можно обнаружить с помощью спектральных наблюдений в течение нескольких ночей. Излучение одного компонента такой звездной системы с определенной периодичностью смещается то в красную, то в синюю часть спектра в зависимости от того, удаляется или приближается звезда. Если спектр второго компонента демонстрирует аналогичные смещения, но в противофазе, то можно утверждать, что перед нами двойная система. Подобное поведение вызвано эффектом Доплера и движением звезды по орбите и позволяет довольно точно определить период ее обращения.

В случае фотометрических двойных звезд мы наблюдаем изменение кривой силы света, то есть отношения светового потока ко времени, из-за того, что звезды затмевают друг друга. Для наблюдения этого явления необходимо, чтобы плоскость орбиты находилась на линии видимости.

Информация, получаемая в ходе наблюдений за двойными системами, меняется в зависимости от типа наблюдения. Расчеты могут быть более или менее сложными, однако принцип остается неизменным. Не будем вдаваться в подробности формул определения массы и обратимся непосредственно к результатам. В случае визуально-двойных звезд мы наблюдаем эллипс обеих и можем рассчитать их массу:

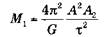
где А1 – большая полуось звезды 1, А2 – большая полуось звезды 2, М1 и М2 – их массы, А = А1 + А2 – расстояние между звездами, τ – период обращения. Эти уравнения выводятся непосредственно из закона Кеплера. Таким образом:

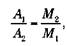
так как центр тяготения должен находиться ближе к более массивной звезде. Если 2 является планетой, М2 << M1 таким образом, число А1 ничтожно мало. Это означает, что А приблизительно равно A2 , и мы получаем закон Кеплера:

Это крайне важно для ситуаций, когда мы не видим звезды с большей массой, например в случае с черной дырой. Именно с помощью этого метода была вычислена масса черной дыры, находящейся в центре Млечного Пути.

В случае спектрально-двойных звезд можно рассчитать только массы, помноженные на наклон орбиты i, или угол между плоскостью орбиты и лучом зрения.

Если двойные звезды одновременно и спектральны, и фотометричны, могут быть получены особенно обширные данные. Возможно вычислить наклон орбиты, обе массы, а также расстояние между звездами и их радиусы.

Центр Солнца движется относительно центра тяжести Солнечной системы – барицентра. Это движение определяется двумя наиболее массивными планетами – Юпитером и Сатурном – и имеет вид почти круговых движений, согласованных с периодами обращения этих планет (около 12 и 29,5 года). Солнце удаляется от центра масс Солнечной системы на величину, приблизительно равную диаметру Солнца, и вращение происходит вокруг оси, которая, как кажется, расположена на поверхности планеты. Наблюдая за этим движением, можно сделать вывод о существовании Юпитера, хоть он и невидим.

Этот факт очень полезен при обнаружении планет, не относящихся к Солнечной системе. Боковое смещение не несет особой информационной нагрузки, так как его непросто оценить, а вот движение по эллипсу может быть прослежено с помощью эффекта Доплера. Благодаря этим методам исследования были обнаружены многочисленные планетные системы, находящиеся за пределами Солнечной.

ТЕМНАЯ МАТЕРИЯ ВСЕЛЕННОЙ

Хорошо известные нам протоны и нейтроны принадлежат к семейству частиц, называемых барионами. На современном этапе развития науки ученые полагают, что во Вселенной существуют и другие, более экзотичные компоненты, например небарионная темная материя и темная энергия. На долю барионной материи приходится всего 4 % Вселенной, на темную материю – 21 %, а темная энергия составляет – 75 %. Таким образом, материя, которую мы видим невооруженным глазом или с помощью телескопов, – малая часть того, что на самом деле наполняет Вселенную. Именно на такую мысль наводит серия наблюдений, например анизотропии космического микроволнового фона, ускорения Вселенной, кривой вращения спиральных галактик и др.

Как это связано с законами Кеплера? Темная материя изначально была обнаружена среди галактик, но одно из признанных доказательств ее существования – это вращение спиральных галактик, которое происходит слишком быстро. Если бы их тяготение было создано звездной массой и газом, оно не могло бы удерживать материю, которая движется с такой скоростью, на периферии, то есть большая центробежная сила не может быть уравновешена гравитацией, которую создает видимая материя.

Предположим, что автогравитация компенсируется центробежной силой:

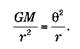
Эта формула подводит нас к третьему закону Кеплера. Мы не можем применить ее сейчас, потому что используем выражение силы тяготения, действующее для точечной центральной массы, например для Солнца, которое представляет собой практически точку в сравнении с размерами Солнечной системы. В пределах галактики материя распределена более равномерно.

Однако, анализируя ее периферию, можно считать, что вся масса сосредоточена в центральной точке. То есть предыдущая формула действительна на периферии и только на ней. Согласно ей:

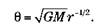
Описываемая этой формулой кривая вращения называется кривой вращения Кеплера.

Однако мы наблюдаем простое вращение, то есть на периферии скорость вращения не зависит от расстояния (см. рисунок на следующей странице). Но это означает, что галактики не повинуются третьему закону Кеплера. Вопрос о том, как это возможно, является одним из самых больших вопросов современной космологии. Если бы движение на периферии спиральных галактик подчинялось предыдущей формуле, согласно которой:

мы легко могли бы рассчитать массу галактики. Но поскольку формула не работает, узнать массу нельзя. Более того, если в первой формуле θ будет постоянной, равенство невозможно: первый член уравнения зависит от r-2 , в то время как второй – от r-1 .

Как можно разрешить этот парадокс, следующий из третьего закона Кеплера? Наиболее распространено следующее объяснение: в галактиках есть большое количество темной материи, которую нельзя увидеть, но которая создает гравитацию. Эта темная материя должна была бы находиться в гало (светящемся кольце) со сферическим распределением, гораздо более расширенным по сравнению с видимой материей диска спиральной галактики. При такой протяженности гало мы уже не могли бы сказать, что наблюдаем за периферией, и это означает, что кеплеровское падение происходит на гораздо больших расстояниях, где уже невозможны наблюдения (см. рисунок).

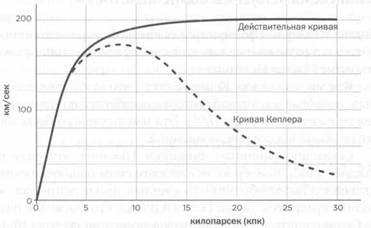
Кривая вращения типичной спиральной галактики. Для маленьких радиусов эта кривая не соответствует кеплеровскому вращению, потому что гравитация не создается точечным центральным телом. Для больших радиусов кривая должна соответствовать кеплеровскому падению, однако она не убывает, а остается постоянной. Скорее всего, это связано с существованием массивного и протяженного гало темной материи.

Масса галактики неизвестна, потому что мы не знаем, какое количество темной материи в ней содержится. Материя темного галактического гало может быть в десять раз больше видимой материи и в десять раз протяженнее.

Существуют и другие теории для объяснения кривой вращения спиральной галактики. Согласно одной из них, неверна либо формула гравитации Ньютона, либо знаменитая формула второго закона Ньютона, F = ma. В обоих случаях третий закон Кеплера не выполнялся бы, поскольку он работает в границах Солнечной системы, но несправедлив для огромных размеров и ускорений, наблюдаемых на периферии галактики. Эта теория называется MOND (Modified Newtonian Dynamics), или модифицированная ньютоновская динамика. Другие теории предполагают, что на движение галактики воздействуют и иные силы, помимо гравитационной, например магнитная.