Пассивные элементы электрической цепи

Пассивный линейный элемент – резистор, имеющий электрическое сопро-

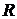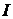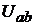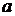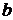тивление (рис. 2.1). Ток и напряжение между точками и (на вы-

водах электрического сопротивления) связаны законом Ома [4]:

(2.1)

Рис. 2.1

Величина, обратная сопротивлению, есть электрическая проводимость

(2.2)

Следующие пассивные элементы – конденсатор и катушка индуктивности − применяются в цепях переменного тока.

Конденсатор обозначают буквой его ёмкость измеряется в фарадах (Ф).

Значение линейной, не зависящей от времени ёмкости, входит в линейное урав-

нение:

(2.3)

Участок цепи с конденсатором представлен на рис. 2.2, а и плоский конденсатор − на рис. 2.2, б.

а б

Рис. 2.2

Ток, текущий через конденсатор, согласно формуле (1.1) равен

(2.4)

Подставляя выражение (2.3) в (2.4) и учитывая, что получим

(2.5)

а обратная зависимость имеет вид

(2.6)

где константа интегрирования, численно равная начальному напряжению

на конденсаторе.

Мгновенная мощность, поступающая в ёмкость, равна

Она связана с накоплением или убыванием электрического заряда в ёмкости.

В конденсаторе ёмкостью , между электродами которого напряжение ,

запасена электрическая энергия

Катушка индуктивности обозначается буквой (рис. 2.3), а её индукив-

ность измеряется в генри (Гн). Линейная, не зависящая от тока, индуктивность входит в линейное уравнение

(2.7)

где магнитный поток через виток катушки (Вб); потокосцепление ка-

тушки в веберах (Вб); количество витков катушки.

Рис. 2.3

Если к катушке с индуктивностью приложить синусоидальное напряже-

ние, то по ней потечёт ток который наведёт в ней ЭДС самоиндукции:

Мгновенное напряжение на индуктивности определяется из выражения

(2.8)

Подставляя уравнение (2.7) в (2.8), получим, учитывая, что

(2.9)

а обратная зависимость имеет вид:

(2.10)

где константа интегрирования, численно равная начальному току, проте-

кающему через катушку индуктивности.

Мгновенная мощность, поступающая в индуктивность, равна

Она связана с процессом изменения энергии магнитного поля.

В магнитном поле уединённой катушки с индуктивностью L, по которой те-

чёт ток , запасается магнитная энергия

При расчёте цепей в режиме постоянного тока, когда напряже

ние на зажимах любой катушки индуктивности, согласно выражению (2.9), рав-

но нулю:

(2.11)

Поскольку напряжение в режиме постоянного тока на конденсаторе неиз-

менно то ток через конденсатор согласно выражению (2.5), бу-

дет равен

(2.12)

Таким образом, при расчёте цепей в режиме постоянного тока индуктивнос-

ти заменяются короткозамкнутыми отрезками, а ёмкости – разомкнутыми. При этом получается так называемая схема замещения цепи для режима постоян-

ного тока.

Схема из элементов представлена на рис. 2.4, а,схема её замещения

показана на рис. 2.4, б.

а б

Рис. 2.4

Схемы, содержащие элементы, часто используются в конструкциях

электрических фильтров − устройств, при помощи которых гармонические сос-

тавляющие токов и напряжений определённой частоты или в пределах опреде-

лённой полосы частот значительно уменьшаются.