Методы расчёта электрических цепей

В.И. КУРИР

МЕТОДЫ РАСЧЁТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

ПОСТОЯННОГО ТОКА

Учебное пособие

Рекомендовано к изданию Учебно-методическим управлением

КНИТУ -КАИ

Казань 2016

УДК621.3 (075.8)

ББК 32я7

К88

Рецензенты:

доктор технических наук, профессор В.Г. Макаров (Казанский национальный

исследовательский технологический университет),

кандидат технических наук, доцент А.Р. Сафин (Казанский государственный энергетический университет)

КУРИР В.И.

К88 Методы расчёта электрических цепей постоянного тока: учебное посо-

бие / В.И. Курир. – Казань: Изд-во КНИТУ-КАИ, 2016. – 112 С.

ISBN

Подготовлено с привлечением ряда учебно-методических пособий по реше-

нию задач электротехники, разработанных крупными отечественными учёны-

ми.

Содержатся основы теории и расчёта линейных электрических цепей посто-

янного тока, приведены решения многих задач.

Предназначено для студентов, изучающих дисциплины электротехнического профиля, в том числе с дистанционной и заочной формами обучения.

Табд. 1 Ил. 77 Библиогр.: 20 назв.

УДК621.3 (075.8)

ББК 32я7

ISBN © В.И. Курир, 2016

© Изд-во НИТУ−КАИ,

ВВЕДЕНИЕ

Представленное учебное пособие предполагалось автором как методичес-

кое пособие по решению задач раздела электротехники «Линейные электричес-

кие цепи постоянного тока». Автор рассматривает представленное учебное по-

собие как необходимое дополнение к лекционным занятиям и в качестве прак-

тикума при решении задач электротехники для студентов элетротехнических факультетов.

Раздел «Линейные электрические цепи постоянного тока» относится к пер-

вой стадии знакомства студентов с теоретическими основами электротехники. Несмотря на преобладание в промышленности электрических машин, аппара-

тов и линий электропередач переменного тока, устройств, работающих на пос-

тоянном токе, немало. На постоянном токе пока работает троллейбус, трамвай, электропоезд, электролизные печи, литейные производства, многочисленный

массив электротехнических измерительных приборов.

В начале приведена теоретическая часть, необходимая для решения задач. Далее следуют задачи с решениями по данной тематике. Основные методы решения задач – классические: метод контурных токов, метод узловых потен-

циалов, метод эквивалентного источника.

Следует отметить, что при решении задач линейных цепей постоянного и переменного токов базисными законами являются одни и те же законы Ома и Кирхгофа. Поэтому раздел «Линейные электрические цепи постоянного тока» является базисным для соответствующего раздела «Линейные электрические цепи переменного тока».

В качестве отправного материала автором использованы известные методи-

ческие разработки советских и российских учёных − электромехаников: А.А.

Бессонова, М.Р. Шебеса, Г.Г. Рекуса и др. Задачи с решениями классифициро-

ваны по разделам, что максимально облегчает студенту ознакомление с метода-

ми решения задач.

Автор нацелен на подготовку аналогичных учебных пособий по другим разделам электротехники и электроники.

Автор считает, что решение задач электротехники на программных комплек-

cах должно войти в обязательную систему обучения студентов электротехни-

ческих специальностей. Образовательная цепочка должна строиться по прин-

ципу: лекция практические занятия (решение задач) решение задач электротехники на ЭВМ лабораторные занятия на учебных стендах.

Автор выражает искреннюю признательность доктору технических наук, профессору А.Ю. Афанасьеву за целый ряд полезных замечаний и внимательность к работе.

БАЗИСНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ

ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Электрическая цепь постоянного тока содержит источники электрической энергии, приёмники электрической энергии, измерительные приборы, коммута-

ционную аппаратуру, соединительные линии и провода [3].

В источниках электрической энергии химическая, тепловая, механическая и другие виды энергии преобразуются в электрическую энергию.

В приёмниках электрической энергии электрическая энергия преобразуется в механическую энергию (двигатели постоянного тока), тепловую (электричес-

кие печи), и химическую (электролизные ванны).

Графическое изображение электрической цепи с помощью условно приня-

тых обозначений, позволяющих приближённо рассчитать процессы в цепи,на-

зывается электрической схемой.

Конфигурация электрической схемы цепи определяется следующими гео-

метрическими понятиями: ветвь, узел, контур. Ветвь схемы состоит из одно-

го или нескольких последовательно соединённых элементов, каждый из кото-

рых имеет два вывода (начало и конец), причём к концу каждого предыдущего элемента присоединяется начало следующего. В узле схемы соединяются три и более число ветвей. Контур − замкнутый участок электрической цепи.

Электрическим током проводимости называется всякое упорядоченное дви-

жение электрических зарядов в проводниках.

Ток численно равен отношению количества электричества 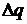, переносимо-

го заряженными частицами через поперечное сечение проводника , к некото-

рому промежутку времени , стремящемуся к нулю:

(1.1)

где ток, измеренный в амперах (А); 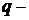заряд в кулонах (Кл); 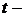время в се-

кундах (с).

За положительное направление электрического тока принимается направле-

ние движения положительных зарядов. В действительности в металлических проводниках электрический ток создаётся движением электронов в направле-

нии, обратном току.

Помимо токов проводимости существуют токи смещения (в диэлектриках) и токи переноса (в электронных лампах). Токи смещения возникают при перио-

дическом изменении напряжённости электрического поля (например, в конден-

саторе).

Постоянным током называют ток, неизменный во времени. Постоянный ток принято обозначать буквой 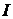,ЭДС источника , сопротивление 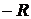, прово-

димость 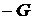. В международной системе единиц (СИ) единица тока − ампер (А), единица ЭДС − вольт (В), единица сопротивления − ом (Ом), единица про-

водимости − сименс (См).

Электрическое поле, созданное электрическими зарядами, оказывает сило-

вое воздействие на соседние электрические заряды. В теории элетростатическо-

го и стационарного электрического поля введена силовая характеристика поля

− напряжённость электрического поля − (В/м). В электростатическом и ста-

ционарном электрическом полях на заряд действует сила Отсюда

следует, что определяется как силовая характеристика поля Ес-

ли заряд под действием сил поля переместится из точки 1в точку 2, то силы поля совершат работу , где − направленный отрезок, элемент пути из 1 в 2.

Потенциалом 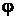некоторой точки электрической цепи называют величину, равную отношению потенциальной энергии 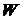, которой обладает заряд на-

ходящийся в данной точке, к этому заряду 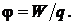Потенциальная энергия 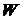равна энергии, расходуемой зарядом при его перемещении из данной точки

электрической цепи в точку, имеющую нулевой потенциал. В электрической

цепи за точку с нулевым потенциалом обычно принимают заземлённую точку,

обозначаемую на схемах знаком заземления. На интегральных микросхемах такая точка обозначается буквами или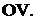

Под разностью потенциалов 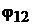между точками 1 и 2 понимают работу, совершаемую силами поля при переносе заряда q = 1 Кл из точки 1 в точку 2,

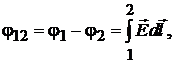(1.2)

где 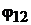не зависит от того, по какому пути происходило перемещение из точ-

ки 1 в точку 2. Выражению (1.2) соответствует дифференциальное соотноше-

ние

(1.3)

Электрическое поле называют потенциальным, безвихревым, если для него

(1.4)

После проведения подстановки уравнения (1.3) в (1.4) получим: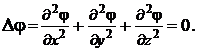

Электрическое поле постоянного тока − безвихревое, потенциальное, как и электростатическое.

Электрическим напряжением называется разность потенциалов между дву-

мя точками электрической цепи:

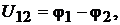(1.5)

где потенциалы точек1 и 2 в вольтах (В). В электротехнике разность потенциалов на участке цепи называют либо напряжением на данном участке, либо падением напряжения.

Мгновенными электрическими величинами называются величины, зависящие

от времени. Мгновенные величины принято обозначать малыми (строчными)

буквами. Например:

− мгновенное значение заряда;

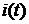− мгновенное значение тока;

− мгновенное значение напряжения;

мгновенное значение мощности.

В ряде случаев буква « t » может быть опущена.

Если в электрических цепях течёт постоянный ток, не меняющийся во вре-

мени, то такие цепи называют цепями постоянного тока. Если в электрической цепи течёт переменный ток, т.е. изменяющийся во времени, то такие цепи на-

зывают цепями переменного тока.

МЕТОД ЭКВИВАЛЕНТНОГО ПРЕОБРАЗОВАНИЯ СХЕМ

В ряде случаев расчёт сложной электрической цепи упрощается, если в её схеме замещения заменить группу резистивных элементов другой эквивалент-

ной группой. Взаимная эквивалентность заключается в том, что после замены режим работы остальной части цепи не изменится.

МЕТОД КОНТУРНЫХ ТОКОВ

Метод контурных токов позволяет уменьшить число совместно решаемых

уравнений до 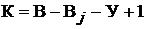. Основан на применении второго закона Кирх-

гофа [1, 3, 6, 7, 9, 11, 12, 14].

Рассмотрим сущность метода сначала для расчёта схемы без источников то-

ка, т. е. при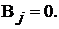

1) выбираем 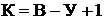независимых контуров и положительных направ-

лений так называемых контурных токов, каждый из которых протекает по всем

элементам соответствующего контура. Достаточным условием выделения 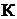независимых контуров является наличие в каждом из них хотя бы одной вет-

ви, принадлежащей только этому контуру;

2) для 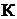независимых контуров составляем уравнения по второму закону

Кирхгофа, совместное решение которых определяет все контурные токи.

3) ток каждой ветви определяем по первому закону Кирхгофа как алгебраи-

ческую сумму контурных токов в соответствующей ветви.

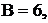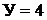В качестве примера рассмотрим расчёт цепи на рис. 9.1, а с числом ветвей узлов , независимых контуров 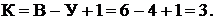Выбира-

ем независимые контуры 1–3 и положительные направления контурных

токов в них (рис.9.1, б). В отличие от токов ветвей каждый контур-

ный ток обозначим двойным индексом номера контура.

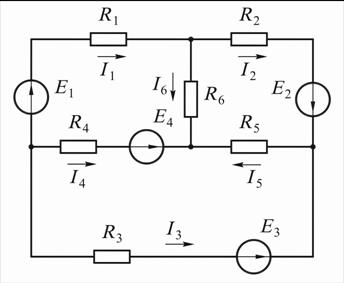
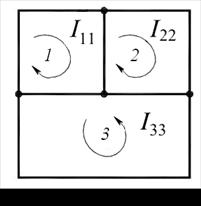
а б

Рис. 9

Уравнения по второму закону Кирхгофа.

Контур 1: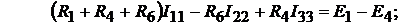

контур 2: 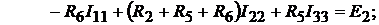(9.1)

контур 3: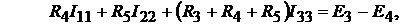

или в матричной форме

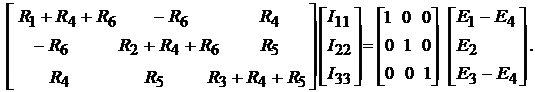(9.2)

Перепишем эти уравнения следующим образом:

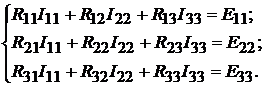(9.3)

Здесь 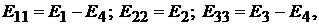где 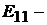контурная ЭДС пер-

вого контура, равная алгебраической сумме ЭДС этого контура; 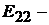контур-

ная ЭДС второго контура; 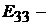контурная ЭДС третьего контура.

Решение системы уравнений (9.1) методом подстановок или (9.2) численны-

ми методами на ЭВМ определяет контурные токи 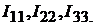Токи ветвей (см. рис. 9.1) находим по первому закону Кирхгофа:

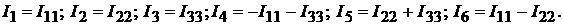
Из выражений (9.1) и (9.2) очевиден принцип составления уравнений по ме-

тоду контурных токов. В левой части уравнений коэффициент при контурном токе рассматриваемого контура положителен и равен сумме сопротивлений его ветвей. Коэффициенты при контурных токах в контурах, имеющих общие вет-

ви с рассматриваемым контуром, равны сумме сопротивлений общих ветвей со знаком плюс (минус), если направления контурных токов в общих ветвях совпадают (противоположны). Правая часть уравнений содержит алгебраичес-

кую сумму ЭДС ветвей рассматриваемого контура, причём слагаемое записыва-

ется со знаком плюс (минус), если направления ЭДС и положительное направ-

ление контурного тока совпадают (противоположны).

Общее решение системы n уравнений относительно тока 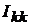может быть

также записано в виде:

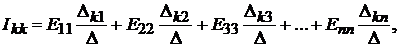(9.4)

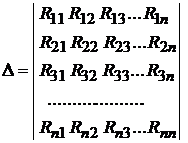где (9.5)

есть определитель системы.

Алгебраическое дополнение 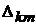получено из определителя 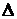путём вычёр-

кивания k-го столбца и m-й строки и умножения полученного определителя

на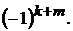

При расчёте схемы замещения с источниками тока возможны упрощения. Контурный ток, выбранный так, что других контурных токов в ветви с источ-

ником тока нет, известен. Поэтому в схеме с 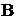ветвями, 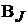из которых содер-

жат источники тока, число независимых контуров без источников тока и соот-

ветствующих им неизвестных контурных токов равно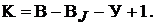

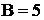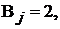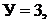Например, в цепи на схеме рис. 9.2 число ветвей с источниками тока узлов независимых контуров без источников тока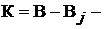 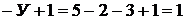(контур 3).

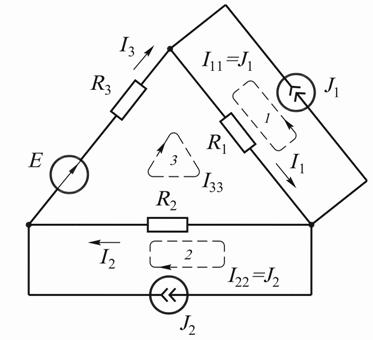
Рис. 9.2

Уравнение по второму закону Кирхгофа для контура 3 при выбранных поло-

жительных направлениях контурных токов:

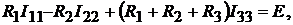
т.е.

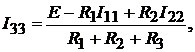
где 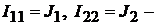известные токи контуров 1 и 2. Токи ветвей:

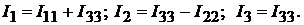
Пример 15.В схеме, изображённой на рис. 9.3, определить токи 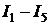в ветвях, напряжения 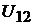и 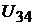между точками 1 – 2 и 3 – 4 цепи. Соста-

вить уравнение баланса мощностей. ЭДС источника питания 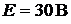(внут-

ренним сопротивлением источника пренебречь), ток источника тока 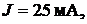сопротивления резисторов: .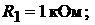

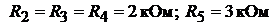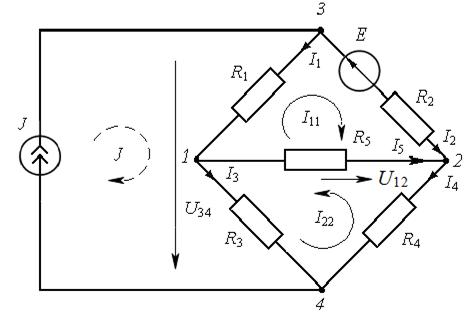
Рис. 9.3

Решение. Условные положительные направления контурных токов в данной электрической цепи принимаем соответствующими рис. 9.3 (показаны сплош-

ными и пунктирными линиями).

По второму закону Кирхгофа составляем уравнение для правого верхнего контура электрической цепи (обход контура по ходу часовой стрелки):

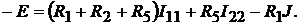
То же для правого нижнего контура:

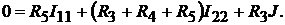
После подстановки значений параметров (ЭДС источника питания, сопро-

тивлений, тока источника тока) получим:

Ток 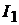совпадает с направлением большего тока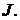

Ток в ветви резистора 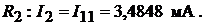Ток в ветви резистора

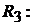
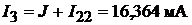. Ток в ветви резистора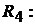 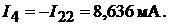Ток в ветви резистора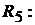 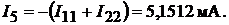Напряжение между узлами 3 и 4 цепи находим из уравнения, составленного в соответствии со вторым законом Кирхгофа для контура 2342: 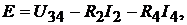откуда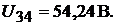

Напряжение между узлами 1 и 2 цепи: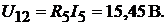

Уравнение баланса мощностей:

,

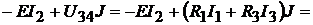
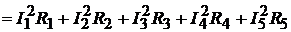откуда после подстановки числовых данных получим тождество:

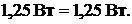
Пример 16.По трёхпроводной линии длиной 500 м. (см. рис. 9.4) от двух генераторов 1 и 2 питаются две группы ламп по 50 Вт, 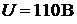. В первой группе 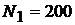ламп, во второй 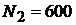ламп. Сечение крайних проводов 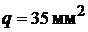, а сечение среднего (нулевого) провода 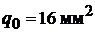. Каждый генератор имеет внутреннее сопротивление 0,01 Ом и развивает ЭДС 120 В. Определить токи во всех проводах линии и напряжение на зажимах каждой группы ламп, сопротивления которых считать постоянными. Материал провода − медь.

Решение. Определим проводимость одной лампы:

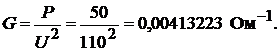
Тогда проводимость 200 ламп равна:

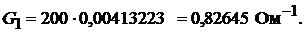
Проводимость 600 ламп равна:

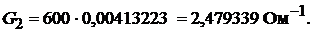
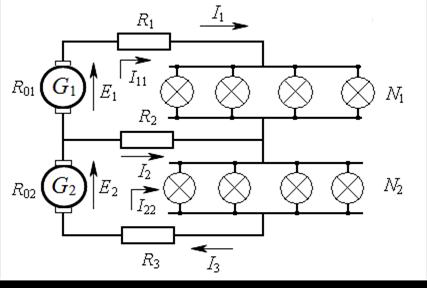
Рис. 9.4

Соответственно сопротивление участка, содержащего 200 ламп, равно:

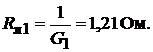
Сопротивление участка, содержащего 600 ламп, равно:

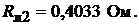
Сопротивления крайних участков линии:

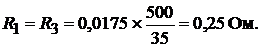
Сопротивление средней (нулевой) линии равно:

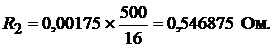
Для определения токов в линиях применим метод контурных токов. Тогда

для верхнего и нижнего контуров получим:

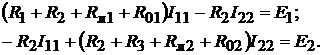
После подстановки численных значений сопротивлений будем иметь:

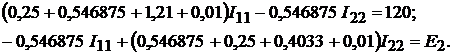
Тогда

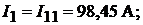
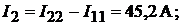
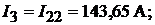
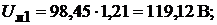
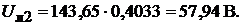
Пример 17. В схеме рис. 9.5 определить все токи методом контурных токов. Дано: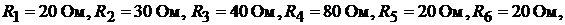

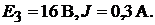
Рис. 9.5

Решение. Выберем контуры для получения независимых уравнений таким образом, чтобы в каждом была по крайней мере одна новая ветвь (показаны на

рис. 9.5 пунктирной линией). Контурными токами будут и .

Запишем уравнения для выбранных токов: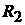

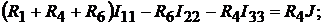
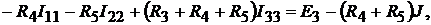
откуда при заданных параметрах находим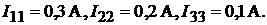

Токи в ветвях: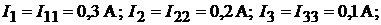

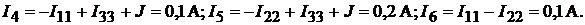
Пример 18.Найти токи в ветвях цепи, изображённой на рис. 9.6, где

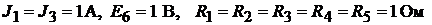
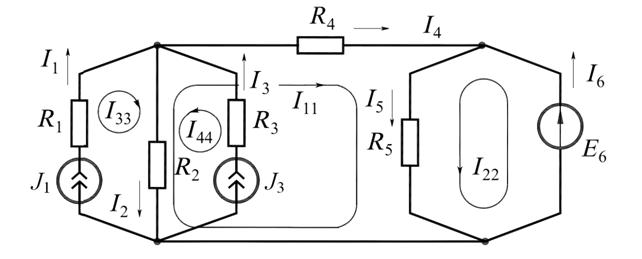
Рис. 9.6

Решение. В цепи четыре независимых контура. В двух ветвях имеются ис-

точники тока с известными токами. Если через каждую из этих ветвей замк-

нуть по одному контурному току, то эти контурные токи автоматически станут известными:

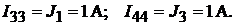
Для определения двух других независимых контурных токов составляем два уравнения:

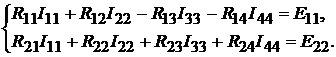
Определяем коэффициенты:

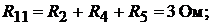
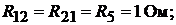
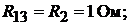
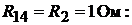
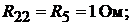
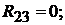
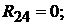
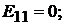
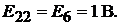
Подставим коэффициенты в левую и правую части вышеуказанного уравне-

ния, получим:

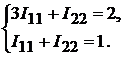
Решив данное уравнение, найдём контурные токи :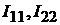

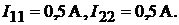
Определяем истинные токи в ветвях:

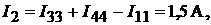
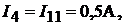
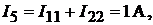
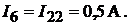
Пример 19.Рассчитаем параметры электрической цепи, схема которой при-

ведена на рис. 9.7, а. Параметры схемы:

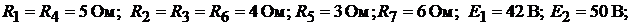
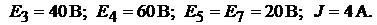
Решение. В схеме четыре узла 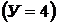и шесть ветвей, не содержащих ис-

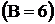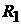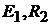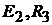
точников тока . Это ветви, состоящие из элементов и 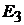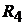и

и 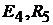, и и 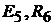. В ветви с элементам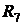и и 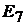тока нет, так как она замыкается на ветвь с вольтметром, сопротивление которого считается беско-

нечно большим. Необходимо определить значения силы тока .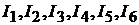

Нумерация узлов, произвольно выбранные положительные направления токов и обходов контуров показаны на рис. 9.7, б.

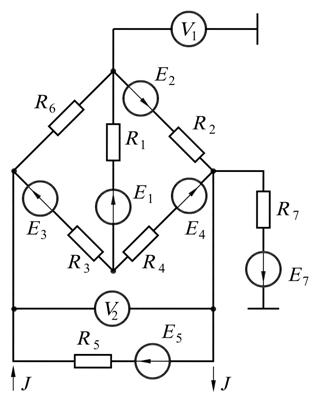
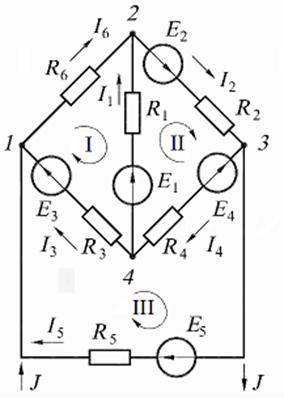
а б

Рис. 9.7

1.По первому закону Кирхгофа составляем 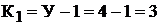независмые узловые уравнения для узлов 1, 2 и 3:

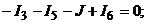
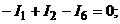
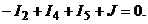
По второму закону Кирхгофа составляем 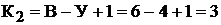кон-

турные уравнения. Для контуров (см. рис. 9.7, б) уравнения имеют вид:

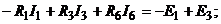
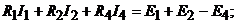
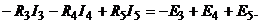
2. Контуры и направления контурных токов в них показаны на рис. 9.8. Кон-

тур с известным контурным током 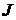проведём по ветви с элементами .

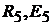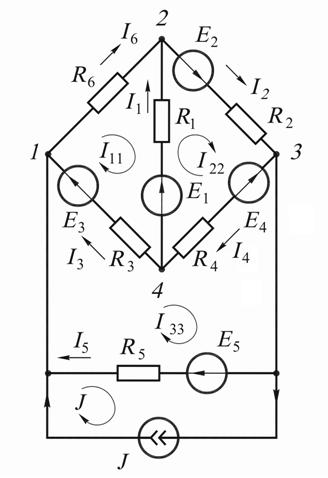
Рис. 9.8

Система уравнений для контурных токов 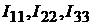имеет вид:

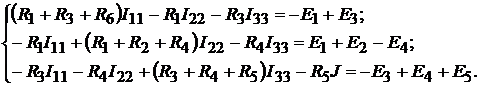
Подставив известные числовые значения, получим:

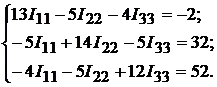
Отсюда получим значения контурных токов: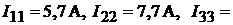

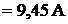. Далее определим силу тока в ветвях:

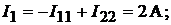
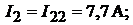
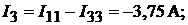
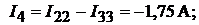
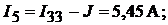
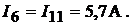
Поскольку значения токов рассчитаны методом контурных токов, то первый закон Кирхгофа выполняется автоматически. Чтобы убедиться в правильности решения проверим тождественность уравнений, составленных по второму зако-

ну Кирхгофа для контуров 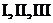, (см. рис. 9.7, б) подставляя в них числовые значения:

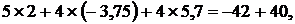или

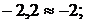
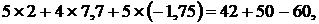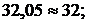
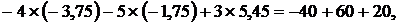или

или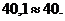

3. Уравнение баланса мощностей для схемы на рис. 9.8 имеет вид

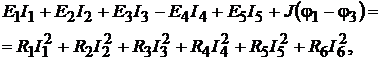
где 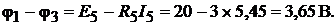Левая часть уравнения учитыва-

ет мощность источников, правая − мощность, потребляемую сопротивления-

ми. Подставив численные значения, получим для левой части:

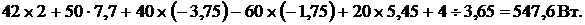
для правой:

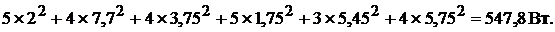
Сравним полученные значения: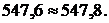

4.Напряжение, измеряемое вольтметром 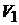, включённым в соответствии с рис. 9.7, а, составляет

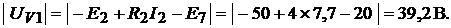
Для вольтметра :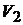

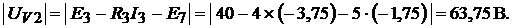
Пример 20.Для обобщённой цепи, приведённой на рис. 9.9, требуется вы-

полнить расчёт цепи с использованием одного из способов расчёта цепи, рас-

считать напряжение между точками A и B схемы, а также составить баланс мощностей для исходной схемы.

Дано: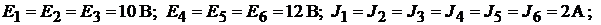

Решение. Проводим расчет схемы с использованием метода контурных то-

ков. Условные направления принятых контурных токов приведены на рис. 9.9.

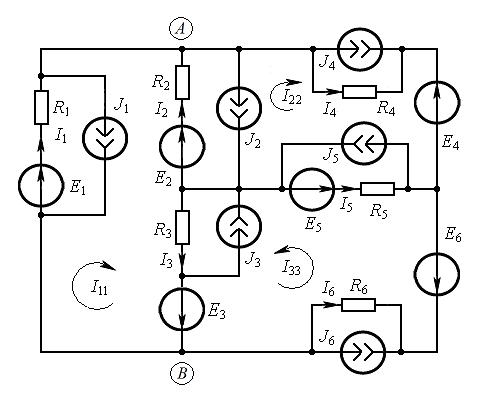
Рис. 9.9

Cистема уравнений, позволяющая определить контурные токи 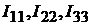, примет вид:

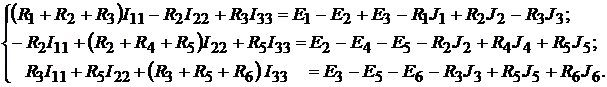
После подстановки численных величин, получим:

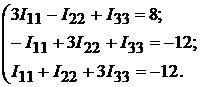
Данные контурные токи равны: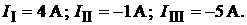

Тогда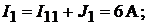

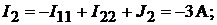
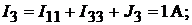
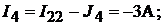
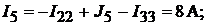
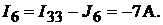
Напряжение между точками A и B схемы:

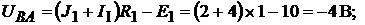
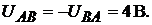
Составим баланс мощностей для исходной схемы.

Мощность, отдаваемая в цепь источниками ЭДС:

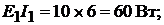
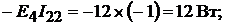
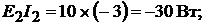
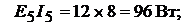
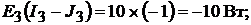
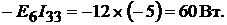
Всего: 188 ВТ.

Мощность, отдаваемая в цепь источниками тока:

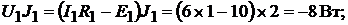
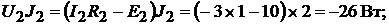
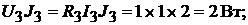
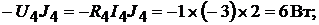
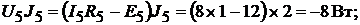
Всего: −20Вт.

Мощность приёмников энергии:

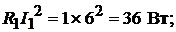
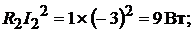
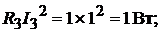
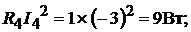
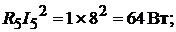
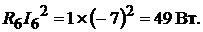
Всего: 168 Вт.

Баланс энергии: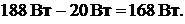

ТЕОРЕМА ВЗАИМНОСТИ

Теорема взаимности формулируется следующим образом [1]: для любой ли -

нейнойцепи ток в k-ветви, вызванный источником ЭДС 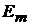, находящимся в

m-ветви, 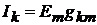равен току 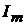в m-ветви, вызванному источником ЭДС 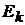(численно равной ЭДС 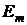), находящимся в k-ветви,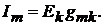

Для доказательства теоремы взаимности обратимся к рис. 11.1, а. Как и при выводах в главее 11, выделим две ветви схемы: ветвь k и ветвь m. Включим в

ветвь m источник ЭДС 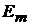, в ветвь 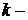амперметр A для измерения тока .

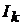Допустим, что каждая из ветвей k и m входит соответственно только в k- и m-

контуры, поэтому по методу контурных токов 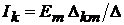. Поменяем мес-

тами источник ЭДС и амперметр, т.е. источник ЭДС переместим из ветви m в ветвь 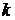и назовём теперь 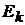, а амперметр – из ветви k в ветвь m. В этом случае ток .

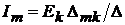Так как 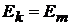, а 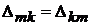в силу симметрии определителя системы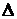

относительно главной диагонали (см. главу 9), то ток 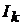в схеме на рис. 11.1, б равняется току 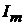в схеме на рис. 11.1, в.

При практическом использовании теоремы взаимности важно иметь в виду взаимное соответствие направлений токов и ЭДС в схемах на рис. 11.1, б, в.

Так, если ЭДС 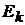источника ЭДС, находящегося в k-ветви схемы рис. 11.1, в,

направлена согласно с контурным током 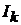в схеме рис. 11.1, б, то положи-

тельное направление отсчёта для тока 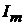в схеме рис. 11.1, в будет совпадать с положительным направлением контурного по ветви тока m (ЭДС 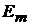в схеме

на рис. 11.1, б направлена по ).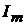

Пример 23.В схеме на рис. 12.1переключател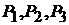и и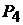могутнахо-

диться в первом или втором положении. Если они находятся в положении 1, то включен только один источник ЭДС 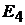.Под действием ЭДС 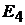протекают токи 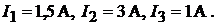Найти ток 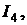если все переключатели нахо-

дятся в положении 2, полагая, что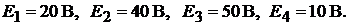

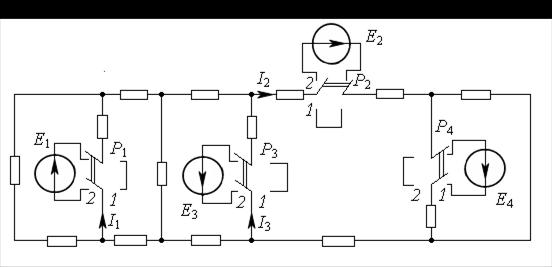
Рис. 12.1

Решение. Для определения тока 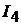воспользуемся принципами наложения и взаимности. Пусть в схеме был включен один источник ЭДС 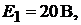а остальные 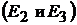отсутствовали, то в ветви 4 (номер ветви соответствует индексу ЭДС) по принципу взаимности протекал бы сверху вниз ток в 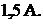Аналогичным образом найдем токи в ветви 4 при включении источников ЭДС 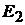и 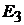и произведём алгебраическое сложение частичных токов (с учётом их направления):

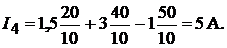
Все искомые величины найдены.

ТЕОРЕМА КОМПЕНСАЦИИ