Терминология, применяемая в теории надежности

ВВЕДЕНИЕ

Обоснование необходимого уровня надежности систем электроснабжения имеет большое народнохозяйственное значение, поскольку перерывы в подаче электроэнергии могут привести к значительному материальному ущербу потребителей и другим негативным явлениям.

В настоящее время при проектировании и эксплуатации систем электроснабжения промышленных и сельскохозяйственных потребителей методы оценки показателей надежности не нашли должного распространения, что приводит в ряде случаев к принятию неоптимальных решений.

Проблема надежности технических систем была сформулирована в начале 1950-х годов применительно к радиоэлектронным устройствам и системам автоматики. Однако системы электроснабжения имеют специфические особенности построенияифункционирования.

Работу системы электроснабжения можно представить как непрерывный обмен энергией межу системой и потребителями при невозможности ее складирования и непреднамеренных мешающих воздействиях на систему, приводящих к отказу элементов, а в некоторых случаях и системы в целом.

Взаимодействия между системой электроснабжения и внешнейсредой носят стохастический характер, и говорить о бесперебойной подаче электроэнергии можно только с некоторой вероятностью достижения поставленной цели.

В данном учебном пособии с единых методических позиций излагаются основы теории надежности применительно к системам электроснабжения промышленных и сельскохозяйственных потребителей, влияние внешних факторов на работу электроустановок, методические рекомендации по оценке ущерба от перерывов электроснабжения, а также возможные пути повышения надежности при проектировании и эксплуатации.

Цель учебного пособия — помочь студентам в изучении накопленного опыта использования современных методов для оценки надежности.

1. ОБЩИЕ СВЕДЕНИЯ О ТЕОРИИ НАДЕЖНОСТИ
СИСТЕМ ЭЛЕКТРОСНАБЖЕНИЯ

Вопросы для самопроверки

1. Надежность электроснабжения и ее составляющие.

2. Состояние объекта с позиции теории надежности.

3. Отказ. Классификация отказов.

4. Восстанавливаемые и невосстанавливаемые объекты.

5. Способы повышения надежности систем электроснабжения.

6. Категории надежности электроснабжения потребителей.

7. Особенности формировании схем электрических сетей с учетом категории надежности электроснабжения потребителей.

ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Основные понятия

Событие. Вероятность события

Под событием в теории вероятностей понимается всякийфакт, который в результате опыта можетпроизойти или не произойти.Каждое из событий обладает степенью возможности: одни – большей, другие – меньшей. Чтобы количественно сравнивать междусобой события по степени ихвозможности, нужно с каждымсобытием связать определенное число, которое тем больше, чем болеевозможно событие. Такое число назовем вероятностью события. Такимобразом, вероятность события есть численная мера степени объективнойвозможности этого события. Понятие вероятности события всамой своей основе связано с опытным, практическим понятием частотысобытия.

Сравнивая между собой различные события по степени их возможности,необходимо установить какую-то единицу измерения. В качестветакой единицы измерения естественно принять вероятностьдостоверного события, т.е. такого события, которое в результате опытанепременно должно произойти.

Если приписать достоверному событию вероятность, равную единице,то все другие события – возможные, но не достоверные – будутхарактеризоваться вероятностями, меньшими единицы, составляющимидолю единицы.

Противоположностью по отношению к достоверному событиюявляется невозможное событие, т.е. такое событие, которое в данномопыте не может произойти.

Вспомогательные понятия

1. Полная группа событий – несколько событий в данном опыте образуют полную группу событий,если в результате опыта непременно должно появиться хотя быодно из них.

2. Несовместные события – несколько событий называются несовместнымив данном опыте,если никакие два из них не могут появиться вместе.

3. Равновозможные события – несколько событий в данном опыте называются равновозможными,если по условиям симметрии есть основания считать, что ни одно из этих событий не является объективно более возможным, чем другие.

Случайная величина

Одним из важнейших основных понятий теории вероятностей являетсяпонятие о случайной величине.

Случайной величинойназывается величина, которая в результатеопыта может принять то или иное значение, причем неизвестно заранее,какое именно.

Случайные величины, принимающие только отделенные друг отдруга значения, которые можно заранее перечислить, называются дискретнымислучайными величинами.

Случайные величины, возможные значения которых непрерывнозаполняют некоторый промежуток, называются непрерывными случайнымивеличинами.

Если классическая теория вероятностей оперировала по преимуществус событиями, то современная теория вероятностей предпочитаетоперировать со случайными величинами.Случайная величина в отличие от случайного события несет более полную информацию о явлении.

2.1.5. Практически невозможные
и практически достоверныесобытия

На практике обычно приходится иметь дело не с невозможными идостоверными событиями, а с так называемыми практически невозможнымии практическими достоверными событиями.

Практически невозможным событиемназывается событие, вероятностькоторого не в точности равна нулю, но весьма близка к нулю.

Практически достоверным событиемназывается событие, вероятностькоторого не в точности равна единице, но весьма близка кединице.

Вопрос о том, насколько мала должна быть вероятность события,чтобы его можно было считать практически невозможным, выходит зарамки математической теории и в каждом определенном случае решаетсяиз практических соображений в соответствии с той важностью, которуюимеет для нас желаемый результат опыта.

Основные теоремы

Назначение основных теорем

На практике обычно требуется определять вероятности событий,непосредственное экспериментальное воспроизведение которых затруднено.Такая оценка производится для того, чтобы выявить наиболее рациональныеконструктивные параметры элементов проектируемой, перспективнойтехники.

Поэтому, как правило, для определения вероятностей событийприменяются не непосредственные прямые методы, а косвенные, позволяющиепо известным вероятностям одних событий определять вероятностидругих событий, связанных с ними. Теория вероятностей, в основном,и представляет собой систему таких косвенных методов, пользованиекоторыми позволяет свести необходимый эксперимент к минимуму.

Применяя эти косвенные методы, мы всегда в той или иной формепользуемся основными теоремамитеории вероятностей. Этих теоремдве: теорема сложения вероятностей и теорема умножения вероятностей.

Перед тем как формулировать основные теоремы, введем вспомогательныепонятия о сумме событий и произведении событий.

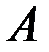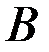Суммой двух событий и называется событие 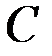, состоящее ввыполнении события 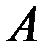или события 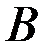, или обоих вместе.

Если события 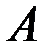и 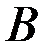несовместны, то появление обоих этих событийвместе отпадает, и сумма событи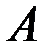й и 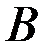сводится к появлению илисобытия 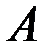, или события .

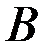Другими словами, суммой двух событи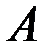й и 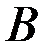называется событие 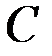, состоящее в появлении хотя бы одного из событи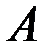й и .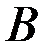

Суммой нескольких событий называется событие, состоящее впоявлении хотя бы одного из этих событий.

Произведением двух событи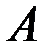й и 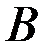называется событие 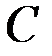, состоящеев совместном выполнении события 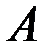и события .

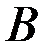Произведением нескольких событий называется событие, состоящеев совместном появлении всех этих событий.

При пользовании понятиями суммы и произведения событий частооказывается полезной наглядная геометрическая интерпретация этихпонятий, которая приведена на рис. 2.1.

Рисунок 2.1 –Сумма двух событий (а); произведение двух событий (б)

Формула полной вероятности

Формула полной вероятности является следствием обеих основныхтеорем – теоремы сложения вероятностей и теоремы умножения вероятностей.

Пусть требуется определить вероятность некоторого события 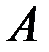, которое может произойти вместе с одним из событий:

,

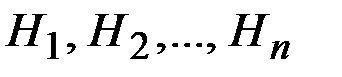образующих полную группу несовместных событий. Будем эти событияназывать гипотезами.

Так как гипотезы 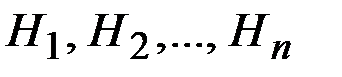образуют полную группу, то событие 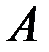может появиться только в комбинации с какой-либо из этих гипотез:

.

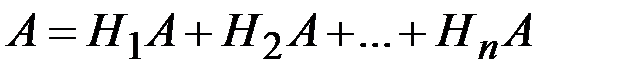Так как гипотезы 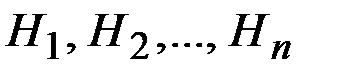несовместны, то и комбинации 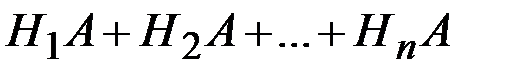также несовместны. Применяя к ним теоремусложения вероятностей, получаем:

.

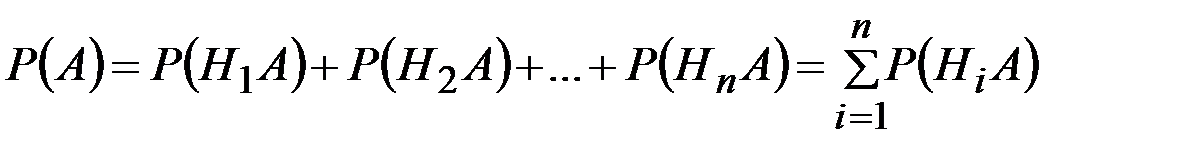Применяя к событию 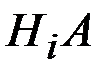теорему умножения, получим:

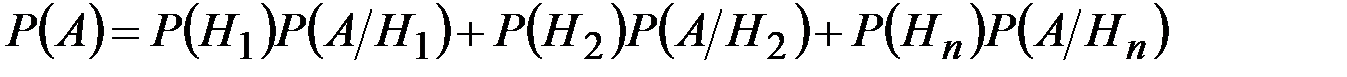
или

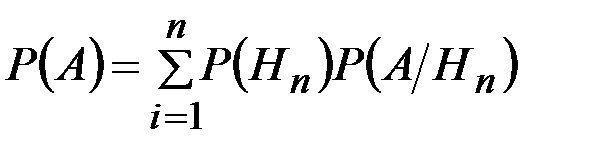. (2.14)

Полученная формула (2.14) и есть формула полной вероятности.

2.2.5. Теорема гипотез (формула Бейеса)

Следствием теоремы умножения и формулы полной вероятностиявляется так называемая теорема гипотез или формула Бейеса.

Поставим задачу.

Имеется полная группа несовместных гипотез 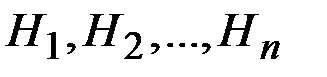. Вероятностиэтих гипотез до опыта известны и равны, соответственно, 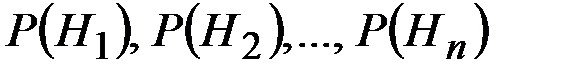. Произведен опыт, в результате которого имеломесто событие 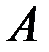. Спрашивается, как следует изменить вероятности гипотезв связи с появлением этого события?

Речь идет о том, чтобы найти условную вероятность 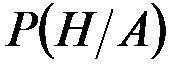длякаждой гипотезы.

Из теоремы умножения имеем:

,

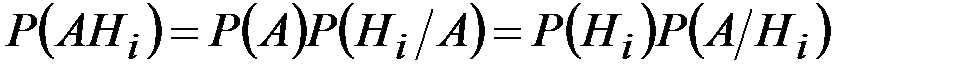где 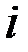=1, 2,…, .

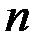Из последнего уравнения, отбрасывая левую часть, находим:

.

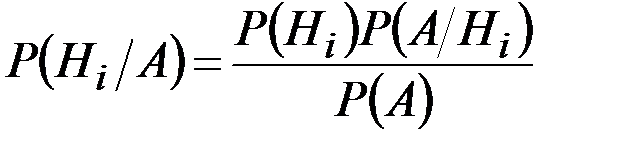Выражая 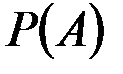с помощью формулы полной вероятности (2.14),имеем:

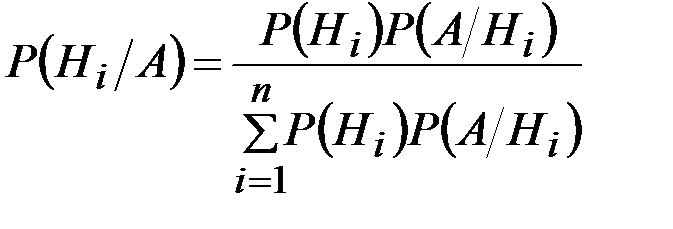. (2.15)

Формула (2.15) и носит название формулы Бейеса или теоремы гипотез.

Функция распределения

Для непрерывной случайной величины не существует ряда распределенияв том смысле, в каком он существует для дискретной величины.Однако различные области возможных значений случайной величины всеже не являются одинаково вероятными, и для непрерывной величины существуетраспределение вероятностей, хотя и не в таком смысле, какдля дискретной.

Для количественной характеристики этого распределения вероятностейудобно пользоваться не вероятностью события 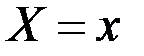, а вероятностьюсобытия 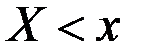, где 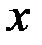–некоторая текущая переменная. Вероятностьэтого события, очевидно, зависит от 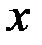, есть некоторая функция от 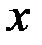.Эта функция называется функцией распределения случайной величины 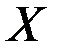и обозначается :

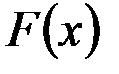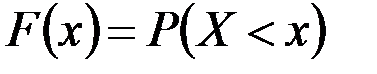. (2.17)

Функцию распределения 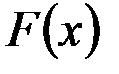иногда называют также интегральнойфункцией распределения или интегральным законом распределения.

Функция распределения – самая универсальная характеристикаслучайной величины. Она существует как для дискретных случайныхвеличин, так и для непрерывных. Функция распределения полностьюхарактеризует случайную величину с вероятностной точки зрения, т.е.является одной из форм закона распределения.

Свойства функции распределения:

1. Функция распределения 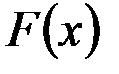есть неубывающая функция своегоаргумента, т.е. при , .

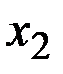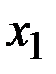
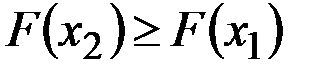2. На минус бесконечности функция распределения равна нулю,т.е. .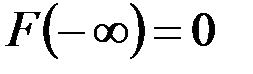

3. На плюс бесконечности функция распределения равна единице,т.е. .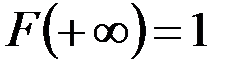

График функции распределения 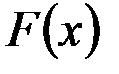в общем случае представляетсобой график неубывающей функции, значения которой начинаются от 0 и доходят до 1, причем в отдельных точках функция может иметьскачки.

Зная ряд распределения дискретной случайной величины, легкопостроить ее функцию распределения. Действительно,

,

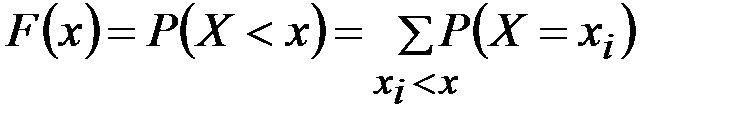где неравенство 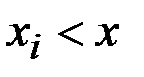под знаком суммы, указывает, что суммированиераспространяется на все те значения 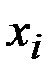, которые меньше .

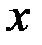Функция распределения любой дискретной случайной величинывсегда есть разрывная ступенчатая функция, скачки которой происходятв точках, соответствующих возможным значениям случайной величины,и равны вероятностям этих значений (рис. 2.5 а). Сумма всех скачков функции 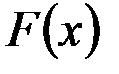равна единице.

По мере увеличения числа возможных значений случайной величиныи уменьшения интервалов между ними число скачков становитсябольше, а сами скачки – меньше; ступенчатая кривая становится болееплавной (рис. 2.5 б). Случайная величина постепенно приближается кнепрерывной, а ее функция распределения – к непрерывной функции(рис. 2.5 в).

Рисунок 2.5 – Функции распределения случайных величин

2.3.3. Вероятность попадания случайной величины
на заданный участок

На практике часто оказывается необходимым вычислять вероятностьтого, что случайная величина примет значение, заключенное в некоторыхпределах, например от 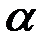до 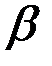. Это событие будем называть попаданием случайной величины 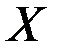на участок от 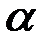до .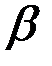

Условимся для определенности левый конец 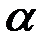включать в участок 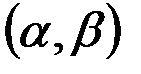, а правый - не включать. Тогда попадание случайной величины 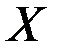на участок 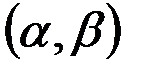равносильно выполнению неравенства:

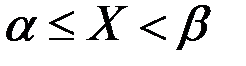
Выразим вероятность этого события через функцию распределениявеличины 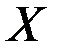. Для этого рассмотрим три события:

событие 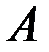, состоящее в том, что ;

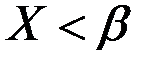событие 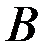, состоящее в том, что ;

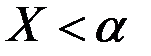событие 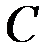, состоящее в том, что .

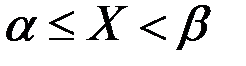Учитывая, что 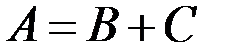, по теореме сложения вероятностей имеем:

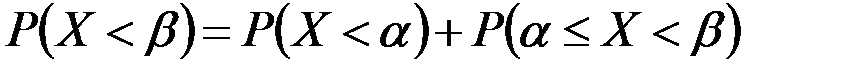
или

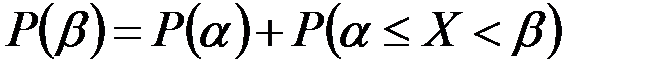
откуда

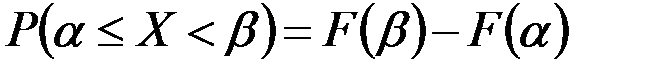, (2.18)

т.е. вероятность попадания случайной величины на заданный участокравна приращению функции распределения на этом участке.

Будем неограниченно уменьшать участок 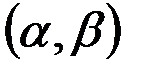, полагая, что 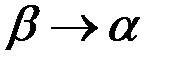. В пределе вместо вероятности попадания на участок получимвероятность того, что величина примет отдельно взятое значение :

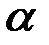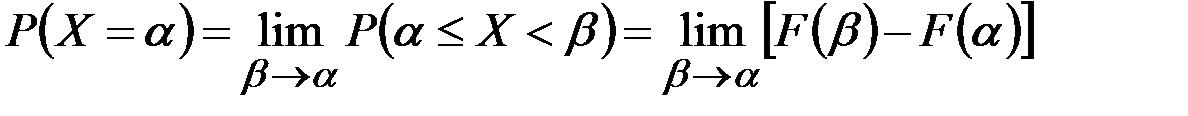. (2.19)

Значение этого предела зависит от того, непрерывна ли функция 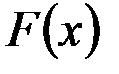в точке 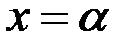или же терпит разрыв. Если в точке 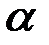функция 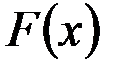имеет разрыв, то предел (2.18) равен значению скачка функции 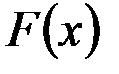в точке 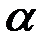. Если же функция 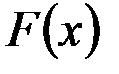в точке 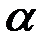непрерывна, то этот пределравен нулю. Отсюда можно сформулировать следующее положение:

Вероятность любого отдельного значения непрерывной случайнойвеличины равна нулю. Другими словами, при непрерывномраспределении вероятностей вероятность попадания на сколь угодномалый участок может быть отлична от нуля, тогда как вероятность попаданияв строго определенную точку в точности равна нулю.

Из того, что событие 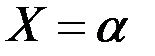имеет вероятность, равную нулю, вовсене следует, что это событие не будет появляться, т.е. что частотаэтого события равна нулю. Известно, что частота события при большомчисле опытов не равна, а только приближается к вероятности. Из того,что вероятность события 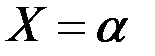равна нулю, следует только, что при неограниченномповторении опыта это событие будет появляться скольугодно редко.

Плотность распределения

Пусть имеется непрерывная случайная величина 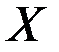с функциейраспределения 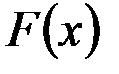(рис. 2.6), которую предположим непрерывной идифференцируемой.

Рисунок 2.6 – Функция распределения

Вычислим вероятность попадания этой случайной величины научасток от 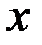до :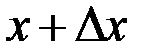

.

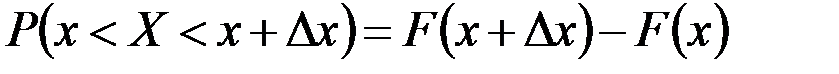т.е. приращение функции распределения на этом участке.

Рассмотрим отношение этой вероятности к длине участка, т.е.среднюю вероятность, приходящуюся на единицу длины на этом участке,и будем приближать 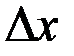к нулю. В пределе получим производнуюот функции распределения:

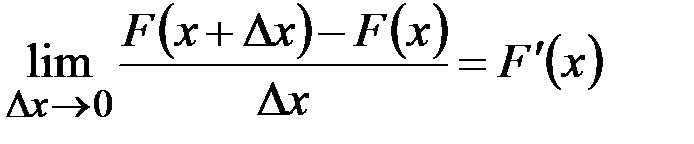. (2.20)

Обозначим

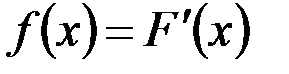. (2.21)

Функция 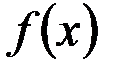– производная функции распределения F\x) по своемусмыслу характеризует как бы плотность, с которой распределяютсязначения случайной величины в данной точке. Эта функция называетсяплотностью распределения или по другому – плотностью вероятности непрерывной случайной величины 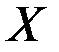. Иногда функцию 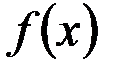называют также дифференциальной функцией распределения илидифференциальным законом распределения величины .

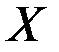Кривая, изображающая плотность распределения случайной величины,называется кривой распределения (рис. 2.7).

Рисунок 2.7 – Кривая распределения

Плотность распределения, так же как и функция распределения,есть одна из форм закона распределения. Но в отличие от функции распределения эта форма не является универсальной: она существует толькодля непрерывных случайных величин.

Рассмотрим непрерывную случайную величину 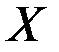с плотностьюраспределения 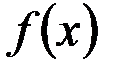и элементарный участок 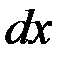, примыкающий к точке 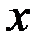(рис. 2.8).

Рисунок 2.8 – Непрерывная случайнаявеличина с плотностьюраспределения 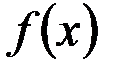на участке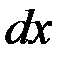

Вероятность попадания случайной величины 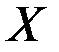на этот элементарныйучасток (с точностью до бесконечно малых высшего порядка)равна 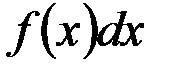. Величина 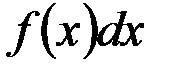называется элементом вероятности.Геометрически это есть площадь элементарного прямоугольника, опирающегосяна отрезок 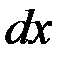(рис. 2.8).

Выразим вероятность попадания величины 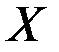на отрезок от 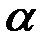до 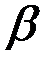(рис. 2.9) через плотность распределения. Очевидно, она равна суммеэлементов вероятности на всем этом участке, т.е. интегралу:

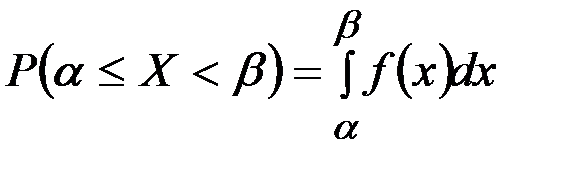. (2.22)

Рисунок 2.9 – Вероятность попадания случайной величины на отрезок от 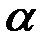до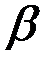

Так как вероятность любого отдельного значения непрерывной случайнойвеличины равна нулю, то в формуле (2.22) можно рассматриватьотрезок 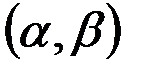, не включая в него левый конец, т.е. отбрасывая знак равенства в .

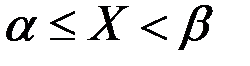Геометрически вероятность попадания величины 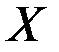на участок 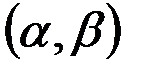равна площади, ограниченной кривой распределения, опирающейсяна этот участок (рис. 2.9).

Выразим функцию распределения через плотность. По определению 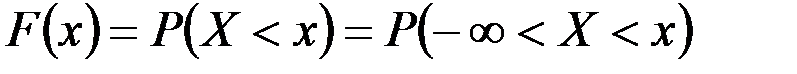откуда по формуле (2.22) имеем:

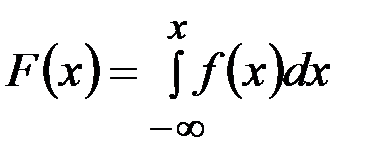. (2.23)

Геометрически 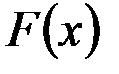есть не что иное, как площадь, образованнаякривой распределения и осью 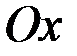, лежащая левее точки 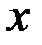. Площадь жевсей фигуры равна 1. Поэтому, если функция 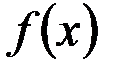сложная и интегралвзять трудно, то для практических целей площадь, или что то же самое,вероятность попадания случайной величины на какой-либо участокможно определить графически.

Формулы (2.21) и (2.23) устанавливают связь между дифференциальнойи интегральной функциями распределения.

Уточним размерности основных характеристик случайной величины – функции распределения и плотности распределения. Функция распределения 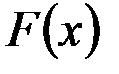, как всякая вероятность, есть величина безразмерная. Размерностьплотности распределения 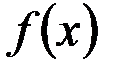,как видно из формулы (2.20), обратна размерности случайной величины.

Таким образом, законами распределения полностью, исчерпывающимобразом описывающих случайную величину с вероятностнойточки зрения, являются:

для дискретной случайной величины:

- функция распределения;

- ряд распределения;

- многоугольник распределения;

для непрерывной величины:

- функция распределения;

- плотность распределения;

- кривая распределения.

Характеристики положения

Прежде всего отметим те характеристики, которые характеризуютположение случайной величины на числовой оси, т.е. указывают некотороесреднее, ориентировочное значение, около которого группируютсявсевозможные значения случайной величины.

Среднее значение случайной величины есть некоторое число, являющеесякак бы ее представителем и заменяющее ее при ориентировочныхрасчетах. Когда мы говорим: средняя нагрузка шинопроводаравна 200 А, то этим указываем определенную числовую характеристикуслучайной величины, описывающую ее местоположение на числовойоси, т.е. характеристику положения.

Из характеристик положения важнейшую роль играет математическоеожидание случайной величины, которое часто называютпросто средним значением случайной величины.

Рассмотрим дискретную случайную величину 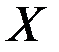, имеющую возможныезначения 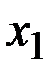, , 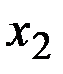,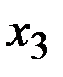…, , 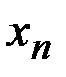с вероятностями 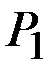, , 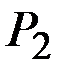,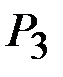…, 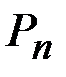. Требуетсяохарактеризовать, каким-то числом положение значений случайнойвеличины на оси абсцисс с учетом того, что эти значения имеютразличные вероятности. Для этой цели воспользуемся так называемымсредним взвешенным из значений 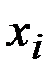причем каждое значение 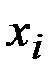приосреднении должно учитываться с весом, пропорциональным вероятностиэтого значения. Таким образом, мы вычислим среднее значениеслучайной величины 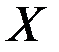, которое обозначим :

,

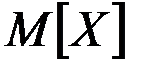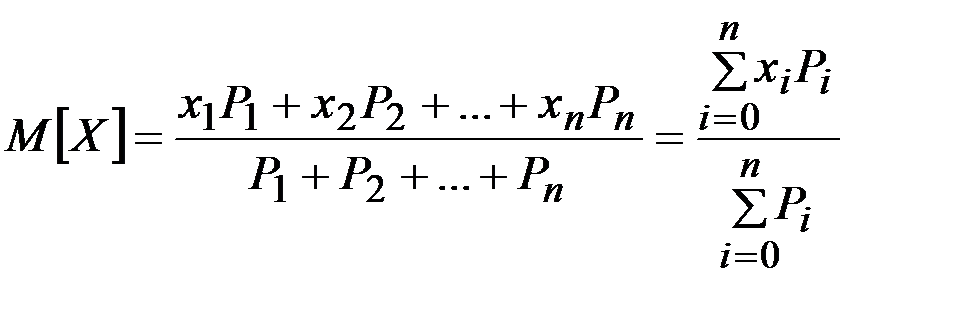или, учитывая, что ,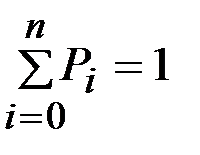

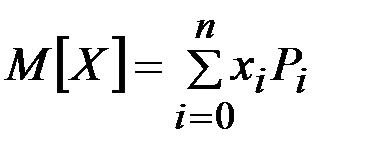. (2.24)

Эго среднее взвешенное значение и называется математическим ожиданиемслучайной величины. Другими словами, математическим ожиданиемдискретной случайной величины называется сумма произведшийвсех возможных значений случайной величины на вероятности этих значений.

Математическое ожидание случайной величины 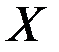связано своеобразнойзависимостью со средним арифметическим статистическихзначений случайной величины при большом числе опытов. Эта зависимостьтакого же типа, как зависимость между частотой и вероятностью,а именно: при большом числе опытов среднее арифметическое статистическихзначений случайной величины приближается (сходится повероятности) к ее математическому ожиданию.

Формула (2.24) для математического ожидания соответствуетслучаю дискретной случайной величины. Для непрерывной величины 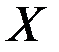математическое ожидание, естественно, выражается уже не суммой, аинтегралом:

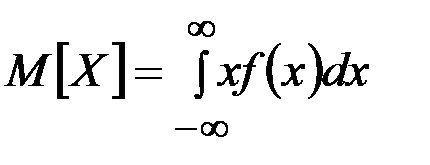, (2.25)

где 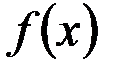– плотность распределения величины .

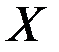Формула (2.25) получается из формулы (2.24), если в ней заменитьотдельные значения 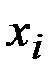непрерывно изменяющимся параметром 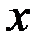,соответствующие вероятности 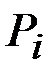, – элементом вероятности 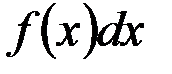, конечнуюсумму – интегралом.

Часто величина 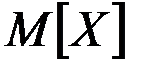входит в формулы как определенное числои ее удобнее обозначать одной буквой. В этих случаях будем обозначатьматематическое ожидание величины 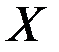через :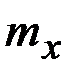

.

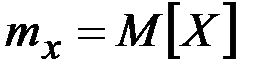Эти обозначения для математического ожидания будут применяться параллельнов зависимости от удобства написания формул.

Отметим ряд теорем о математическом ожидании функций, представляющихпрактические формулы вычисления этой характеристики.

Математическое ожидание неслучайной величины

Если 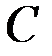– неслучайная величина, то:

.

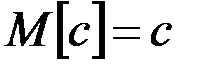Вынесение неслучайной величины за знак математическогоожидания

Если 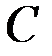– неслучайная величина, а 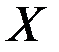– случайная, то

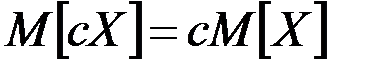
т.е. неслучайную величину можно выносить за знак математическогоожидания.

Математическое ожидание суммы случайных величин:

.

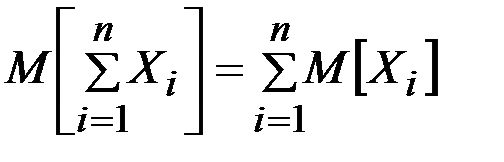т.е. математическое ожидание суммы нескольких случайных величинравно сумме их математических ожиданий.

Математическое ожидание произведения случайных величин:

.

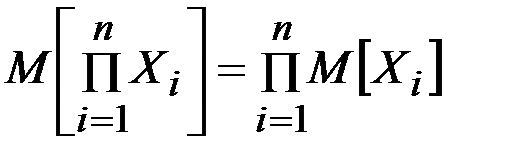т.е. математическое ожидание произведения независимых случайныхвеличин равно произведению их математических ожиданий.

Математическое ожидание функции случайной величины:

;

,

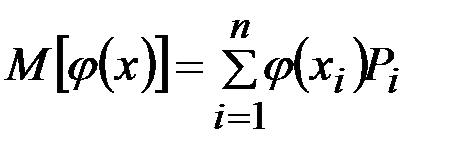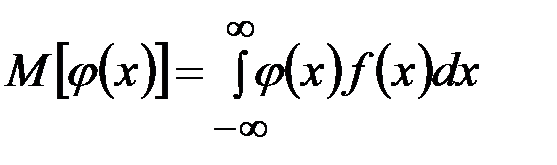соответственно для дискретной и непрерывной величин.

Кроме важнейшей из характеристик положения – математическогоожидания, – иногда применяются и другие характеристики положения,в частности мода и медиана случайной величины.

Модой дискретной случайной величины называется ее наиболеевероятное значение, а для непрерывной величины модой является тозначение, в котором плотность вероятности максимальна (рис. 1.10).Моду принято обозначать буквой .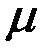

Рисунок 2.10 – Мода дискретной (кривая 1)и мода непрерывной (кривая 2) случайных величин

Если многоугольник распределения или кривая распределенияимеет более одного максимума, то распределение называется полимодальным (рис. 2.11).

Рисунок 2.11 – Полимодальные распределения

Встречаются распределения, обладающие посередине не максимумом,а минимумом (рис. 2.12). Такие распределения называются ангимодальными.

Рисунок 2.12 – Антимодальные распределения

Медианой случайной величины 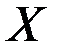называется такое ее значение 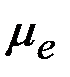, для которого 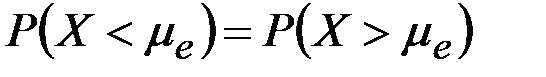, т.е. одинаково вероятно, окажетсяли случайная величина меньше или больше 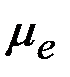Геометрическимедиана – это точка абсциссы, в которой площадь, ограниченная кривойраспределения, делится пополам (рис. 2.13).

Рисунок 2.13 – Медиана случайной величины

2.3.7. Моменты. Дисперсия.
Среднее квадратическое отклонение

Кроме характеристик положения случайной величины употребляетсяеще ряд характеристик. В качестве таких характеристик чаще всегоприменяются так называемые моменты. Наибольшее распространениена практике получили моменты двух видов: начальные и центральные.

Начальным моментом 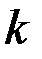-го порядка дискретной случайной величины 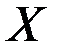называется сумма вида:

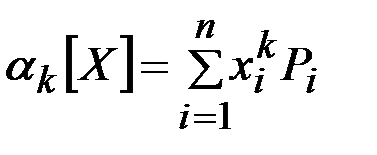. (2.26)

Для непрерывной случайной величины 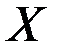начальным моментом 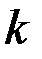-го порядка называется интеграл:

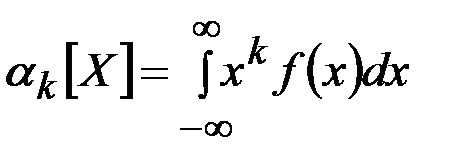. (2.27)

Из формул (2.26) и (2.27) нетрудно убедиться, что введенная ранееосновная характеристика положения – математическое ожидание – представляет собой не что иное, как первый начальный момент случайной величины .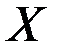

Пользуясь знаком математического ожидания, можно объединитьдве последние формулы и написать общее определение начального момента 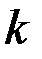-го порядка, справедливое как для дискретных, так и для непрерывныхвеличин:

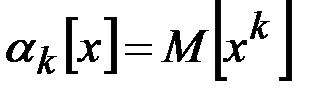, (2.28)

т.е. начальным моментам 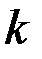-го порядка случайной величины 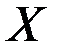называетсяматематическое ожидание 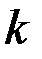-й степени этой случайнойвеличины.

Перед тем как дать определение центрального момента, введемновое понятие центрированной случайной величины.

Пусть имеется случайная величина 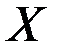с математическим ожиданием 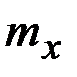. Центрированной случайной величиной, соответствующей величине 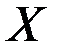, называется отклонение случайной величины 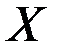от ее математическогоожидания:

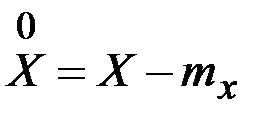. (2.29)

Принято обозначать центрированную случайную величину, соответствующуюданной случайной величине, той же буквой, но со значком «0» наверху.

Легко убедиться, что математическое ожидание центрированнойслучайной величины равно нулю. Действительно, для дискретной величины:

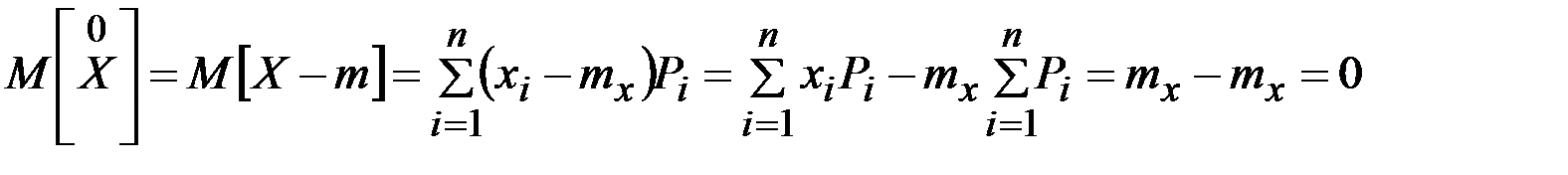
аналогично можно написать и для непрерывной величины.

Центрирование случайной величины, очевидно, равносильно переносуначала координат в среднюю центральную точку абсциссы,которая равна математическому ожиданию.

Моменты центрированной случайной величины носят названиецентральных моментов. Они аналогичны моментам относительноцентра тяжести в механике.

Таким образом, <