Распределение Пирсона (или “хи”-квадрат распределение)
Число: 2085
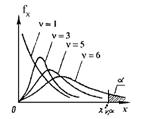 | Пусть СВ 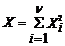 , где Xi ~ N(0, 1) - независимые нормированные нормально распределенные СВ. Тогда X подчиняется распределению “хи”-квадрат с n степенями свободы: X ~ cn2. С ростом n “хи”-квадрат распределение приближается к нормальному с параметрами mX = n и sX = , где Xi ~ N(0, 1) - независимые нормированные нормально распределенные СВ. Тогда X подчиняется распределению “хи”-квадрат с n степенями свободы: X ~ cn2. С ростом n “хи”-квадрат распределение приближается к нормальному с параметрами mX = n и sX = 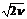 . . |
Таблица 2.
Значения c2n,a в зависимости от числа степеней свободы n и вероятности a:
P{ X > c2n, a } = a.
| число степеней свободы | Вероятность a: | |||||||
| n | 0,99 | 0,975 | 0,95 | 0.90 | 0,10 | 0,05 | 0,025 | 0,01 |
| 0,00016 | 0,00098 | 0,0039 | 0,016 | 2,7 | 3,8 | 5,0 | 6,6 | |
| 0,020 | 0,051 | 0,103 | 0,211 | 4,6 | 6,0 | 7,4 | 9,2 | |
| 0,115 | 0,216 | 0,352 | 0,584 | 6,3 | 7,8 | 9,3 | 11,3 | |
| 0,30 | 0,48 | 0,71 | 1,06 | 7,8 | 9,5 | 11,1 | 13,3 | |
| 0,55 | 0,83 | 1,14 | 1,61 | 9,2 | 11,1 | 12,8 | 15,1 | |
| 0,87 | 1,24 | 1,63 | 2,20 | 10,6 | 12,6 | 14,4 | 16,8 | |
| 1,24 | 1,69 | 2,17 | 2,83 | 12,0 | 14,1 | 16,0 | 18,5 | |
| 1,65 | 2,18 | 2,73 | 3,49 | 13,4 | 15,5 | 17,5 | 20,1 | |
| 2,09 | 2,70 | 3,32 | 4,17 | 14,7 | 16,9 | 19,0 | 21,7 | |
| 2,56 | 3,25 | 3,94 | 4,86 | 16,0 | 18,3 | 20,5 | 23,2 | |
| 3,1 | 3,8 | 4,6 | 5,6 | 17,3 | 19,7 | 21,9 | 24,7 | |
| 3,6 | 4,4 | 5,2 | 6,3 | 18,5 | 21,0 | 23,3 | 26,2 | |
| 4,1 | 5,0 | 5,9 | 7,0 | 19,8 | 22,4 | 24,7 | 27,7 | |
| 4,7 | 5,6 | 6,6 | 7,8 | 21,1 | 23,7 | 26,1 | 29,1 | |
| 5,2 | 6,3 | 7,3 | 8,5 | 22,3 | 25,0 | 27,5 | 30,6 | |
| 5,8 | 6,9 | 8,0 | 9,3 | 23,5 | 26,3 | 28,8 | 32,0 | |
| 6,4 | 7,6 | 8,7 | 10,1 | 24,8 | 27,6 | 30,2 | 33,4 | |
| 7,0 | 8,2 | 9,4 | 10,9 | 26,0 | 28,9 | 31,5 | 34,8 | |
| 7,6 | 8,9 | 10,1 | 11,7 | 27,2 | 30,1 | 32,9 | 36,2 | |
| 8,3 | 9,6 | 10,9 | 12,4 | 28,4 | 31,4 | 34,2 | 37,6 | |
| 8,9 | 10,3 | 11,6 | 13,2 | 29,6 | 32,7 | 35,5 | 38,9 | |
| 9,5 | 11,0 | 12,3 | 14,0 | 30,8 | 33,9 | 36,8 | 40,3 | |
| 10,2 | 11,7 | 13,1 | 14,8 | 32,0 | 35,2 | 38,1 | 41,6 | |
| 10,9 | 12,4 | 13,8 | 15,7 | 33,2 | 36,4 | 39,4 | 43,0 | |
| 11,5 | 13,1 | 14,6 | 16,5 | 34,4 | 37,7 | 40,6 | 44,3 | |
| 12,2 | 13,8 | 15,4 | 17,3 | 35,6 | 38,9 | 41,9 | 45,6 | |
| 12,9 | 14,6 | 16,2 | 18,1 | 36,7 | 40,1 | 43,2 | 47,0 | |
| 13,6 | 15,3 | 16,9 | 18,9 | 37,9 | 41,3 | 44,5 | 48,3 | |
| 14,3 | 16,0 | 17,7 | 19,8 | 39,1 | 42,6 | 45,7 | 49,6 | |
| 15,0 | 16,8 | 18,5 | 20,6 | 40,3 | 43,8 | 47,0 | 50,9 |
T - распределение Стьюдента
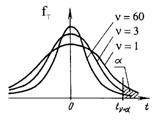 Свойство симметрии: -tn, 1-a= tn, a. Свойство симметрии: -tn, 1-a= tn, a. | Пусть СВ V ~ N(0, 1), а независимая от нее СВ X ~ cn2, тогда СВ 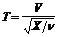 подчиняется t - распределению Стьюдента с n степенями свободы, т.е.: T ~ tn. С ростом n распределение Стьюдента приближается к нормированному нормальному распределению N(0, 1). Уже для n ³ 60 распределение Стьюдента с высокой степенью точности аппроксимируется нормированным нормальным распределением. подчиняется t - распределению Стьюдента с n степенями свободы, т.е.: T ~ tn. С ростом n распределение Стьюдента приближается к нормированному нормальному распределению N(0, 1). Уже для n ³ 60 распределение Стьюдента с высокой степенью точности аппроксимируется нормированным нормальным распределением. |
Таблица 3.
Значения tn, a в зависимости от числа степеней свободы n и вероятности a:
P{ T > tn,a } = a.
| число степеней свободы | Вероятность a: | |||||||
| n | 0,20 | 0,10 | 0,05 | 0,025 | 0,01 | 0,005 | 0,001 | 0,0005 |
| 1,38 | 3,08 | 6,31 | 12,71 | 31,82 | 63,66 | 318,31 | 636,62 | |
| 1,06 | 1,89 | 2,92 | 4,30 | 6,97 | 9,93 | 22,33 | 31,60 | |
| 0,98 | 1,64 | 2,35 | 3,18 | 4,54 | 5,84 | 10,21 | 12,94 | |
| 0,94 | 1,53 | 2,13 | 2,78 | 3,75 | 4,60 | 7,17 | 8,61 | |
| 0,92 | 1,48 | 2,02 | 2,57 | 3,37 | 4,03 | 5,89 | 6,86 | |
| 0,91 | 1,44 | 1,94 | 2,45 | 3,14 | 3,71 | 5,21 | 5,96 | |
| 0,90 | 1,42 | 1,90 | 2,37 | 3,00 | 3,50 | 4,78 | 5,41 | |
| 0,89 | 1,40 | 1,86 | 2,31 | 2,90 | 3,36 | 4,50 | 5,04 | |
| 0,88 | 1,38 | 1,83 | 2,26 | 2,82 | 3,25 | 4,30 | 4,78 | |
| 0,88 | 1,37 | 1,81 | 2,23 | 2,76 | 3,17 | 4,14 | 4,59 | |
| 0,88 | 1,36 | 1,80 | 2,20 | 2,72 | 3,11 | 4,02 | 4,44 | |
| 0,87 | 1,36 | 1,78 | 2,18 | 2,68 | 3,06 | 3,93 | 4,32 | |
| 0,87 | 1,35 | 1,77 | 2,16 | 2,65 | 3,01 | 3,85 | 4,22 | |
| 0,87 | 1,34 | 1,76 | 2,15 | 2,62 | 2,98 | 3,79 | 4,14 | |
| 0,87 | 1,34 | 1,75 | 2,13 | 2,60 | 2,95 | 3,73 | 4,07 | |
| 0,86 | 1,34 | 1,75 | 2,12 | 2,58 | 2,92 | 3,69 | 4,02 | |
| 0,86 | 1,33 | 1,74 | 2,11 | 2,57 | 2,90 | 3,65 | 3,97 | |
| 0,86 | 1,33 | 1,73 | 2,10 | 2,55 | 2,88 | 3,61 | 3,92 | |
| 0,86 | 1,33 | 1,73 | 2,09 | 2,54 | 2,86 | 3,58 | 3,88 | |
| 0,86 | 1,33 | 1,73 | 2,09 | 2,53 | 2,85 | 3,55 | 3,85 | |
| 0,86 | 1 ,32 | 1,72 | 2,08 | 2,52 | 2,83 | 3,53 | 3,82 | |
| 0,86 | 1,32 | 1,72 | 2,07 | 2,51 | 2,82 | 3,50 | 3.79 | |
| 0,86 | 1,32 | 1,71 | 2,07 | 2,50 | 2,81 | 3,48 | 3,77 | |
| 0,86 | 1,32 | 1,71 | 2,06 | 2,49 | 2,80 | 3,47 | 3,75 | |
| 0,86 | 1,32 | 1,71 | 2,06 | 2,48 | 2,79 | 3,45 | 3,73 | |
| 0,85 | 1,31 | 1,70 | 2,04 | 2,46 | 2,75 | 3,39 | 3,65 | |
| 0,85 | 1,30 | 1,68 | 2,02 | 2,42 | 2,70 | 3,31 | 3,55 | |
| 0,85 | 1,30 | 1,67 | 2,00 | 2,39 | 2,66 | 3,23 | 3,46 | |
| 0,84 | 1,29 | 1,66 | 1,98 | 2,36 | 2,62 | 3,16 | 3,37 | |
| ¥ | 0,84 | 1,28 | 1,64 | 1,96 | 2,33 | 2,58 | 3,09 | 3,29 |
F - распределение Фишера
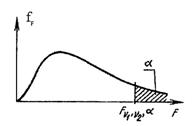 | Пусть СВ X1 ~ cn12, а независимая от нее СВ X2 ~ cn22, тогда СВ 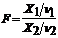 подчиняется F - распределению Фишера с n1 и n2 степенями свободы, т.е.: F ~ Fn1,n2. В таблице 4 приведены значения лишь для a = 0,05, однако, ее можно использовать и при a = 0,95, поскольку Fn1,n2, 1-a = 1/Fn2,n1, a. подчиняется F - распределению Фишера с n1 и n2 степенями свободы, т.е.: F ~ Fn1,n2. В таблице 4 приведены значения лишь для a = 0,05, однако, ее можно использовать и при a = 0,95, поскольку Fn1,n2, 1-a = 1/Fn2,n1, a. |
Таблица 4.
Значения Fn1,n2, a в зависимости от
числа степеней свободы n1, n2 и вероятности a = 0,05: P{ F > Fn1,n2, a } = a.
 n1 n2 n1 n2 | |||||||||
| 18,5 | 19,0 | 19,2 | 19,2 | 19,3 | 19,3 | 19,4 | 19,4 | 19,4 | |
| 10,1 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,89 | 8,85 | 8,81 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,09 | 6,04 | 6,00 | |
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,88 | 4,82 | 4,77 | |
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,21 | 4,15 | 4,10 | |
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,79 | 3,73 | 3,68 | |
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,50 | 3,44 | 3,39 | |
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,29 | 3,23 | 3,18 | |
| 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,14 | 3,07 | 3,02 | |
| 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 3,01 | 2,95 | 2,90 | |
| 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | 2,91 | 2,85 | 2,80 | |
| 4,67 | 3,80 | 3,41 | 3,18 | 3,03 | 2,92 | 2,83 | 2,77 | 2,71 | |
| 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,76 | 2,70 | 2,65 | |
| 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,71 | 2,64 | 2,59 | |
| 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,66 | 2,59 | 2,54 | |
| 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,61 | 2,55 | 2,49 | |
| 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,58 | 2,51 | 2,46 | |
| 4,38 | 3,52 | 3,13 | 2,90 | 2,74 | 2,63 | 2,54 | 2,48 | 2,42 | |
| 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,51 | 2,45 | 2,39 | |
| 4,32 | 3,47 | 3,07 | 2,84 | 2,68 | 2,57 | 2,49 | 2,42 | 2,37 | |
| 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,46 | 2,40 | 2,34 | |
| 4,28 | 3,42 | 3,03 | 2,80 | 2,64 | 2,53 | 2,44 | 2,37 | 2,32 | |
| 4,26 | 3,40 | 3,01 | 2,78 | 2,62 | 2,51 | 2,42 | 2,36 | 2,30 | |
| 4,24 | 3,38 | 2,99 | 2,76 | 2,60 | 2,49 | 2,40 | 2,34 | 2,28 | |
| 4,23 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,39 | 2,32 | 2,27 | |
| 4,21 | 3,35 | 2,96 | 2,73 | 2,57 | 2,46 | 2,37 | 2,31 | 2,25 | |
| 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,45 | 2,36 | 2,29 | 2,24 | |
| 4,18 | 3,33 | 2,93 | 2,70 | 2,55 | 2,43 | 2,35 | 2,28 | 2,22 | |
| 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,33 | 2,27 | 2,21 | |
| 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,25 | 2,18 | 2,12 | |
| 4,00 | 3,15 | 2,76 | 2,53 | 2,37 | 2,25 | 2,17 | 2,10 | 2,04 | |
| 3,92 | 3,07 | 2,68 | 2,45 | 2,29 | 2,17 | 2,09 | 2,02 | 1,96 | |
| ¥ | 3,84 | 3,00 | 2,60 | 2,37 | 2,21 | 2,10 | 2,01 | 1,94 | 1,88 |
 n1 n2 n1 n2 | ¥ | |||||||||
| 19,4 | 19,4 | 19,4 | 19,4 | 19,5 | 19,5 | 19,5 | 19,5 | 19,5 | 19,5 | |
| 8,79 | 8,74 | 8,70 | 8,66 | 8,64 | 8,62 | 8,59 | 8,57 | 8,55 | 8,53 | |
| 5,96 | 5,91 | 5,86 | 5,80 | 5,77 | 5,75 | 5,72 | 5,69 | 5,66 | 5,63 | |
| 4,74 | 4,68 | 4,62 | 4,56 | 4,53 | 4,50 | 4,46 | 4,43 | 4,40 | 4,36 | |
| 4,06 | 4,00 | 3,94 | 3,87 | 3,84 | 3,81 | 3,77 | 3,74 | 3,70 | 3,67 | |
| 3,64 | 3,57 | 3,51 | 3,44 | 3,41 | 3,38 | 3,34 | 3,30 | 3,27 | 3,23 | |
| 3,35 | 3,28 | 3,22 | 3,15 | 3,12 | 3,08 | 3,04 | 3,01 | 2,97 | 2,93 | |
| 3,14 | 3,07 | 3,01 | 2,94 | 2,90 | 2,86 | 2,83 | 2,79 | 2,75 | 2,71 | |
| 2,98 | 2,91 | 2,85 | 2,77 | 2,74 | 2,70 | 2,66 | 2,62 | 2,58 | 2,54 | |
| 2,85 | 2,79 | 2,72 | 2,65 | 2,61 | 2,57 | 2,53 | 2,49 | 2,45 | 2,40 | |
| 2,75 | 2,69 | 2,62 | 2,54 | 2,51 | 2,47 | 2,43 | 2,38 | 2,34 | 2,30 | |
| 2,67 | 2,60 | 2,53 | 2,46 | 2,42 | 2,38 | 2,34 | 2,30 | 2,25 | 2,21 | |
| 2,60 | 2,53 | 2,46 | 2,39 | 2,35 | 2,31 | 2,27 | 2,22 | 2,18 | 2,13 | |
| 2,54 | 2,48 | 2,40 | 2,33 | 2,29 | 2,25 | 2,20 | 2,16 | 2,11 | 2,07 | |
| 2,49 | 2,42 | 2,35 | 2,28 | 2,24 | 2,19 | 2,15 | 2,11 | 2,06 | 2,01 | |
| 2,45 | 2,38 | 2,31 | 2,23 | 2,19 | 2,15 | 2,10 | 2,06 | 2,01 | 1,96 | |
| 2,41 | 2,34 | 2,27 | 2,19 | 2,15 | 2,11 | 2,06 | 2,02 | 1,97 | 1,92 | |
| 2,38 | 2,31 | 2,23 | 2,16 | 2,11 | 2,07 | 2,03 | 1,98 | 1,93 | 1,88 | |
| 2,35 | 2,28 | 2,20 | 2,12 | 2,08 | 2,04 | 1,99 | 1,95 | 1,90 | 1,84 | |
| 2,32 | 2,25 | 2,18 | 2,10 | 2,05 | 2,01 | 1,96 | 1,92 | 1,87 | 1,81 | |
| 2,30 | 2,23 | 2,15 | 2,07 | 2,03 | 1,98 | 1,94 | 1,89 | 1,84 | 1,78 | |
| 2,27 | 2,20 | 2,13 | 2,05 | 2,01 | 1,96 | 1,91 | 1,86 | 1,81 | 1,76 | |
| 2,25 | 2,18 | 2,11 | 2,03 | 1,98 | 1,94 | 1,89 | 1,84 | 1,79 | 1,73 | |
| 2,24 | 2,16 | 2,09 | 2,01 | 1,96 | 1,92 | 1,87 | 1,82 | 1,77 | 1,71 | |
| 2,22 | 2,15 | 2,07 | 1,99 | 1,95 | 1,90 | 1,85 | 1,80 | 1,75 | 1,69 | |
| 2,20 | 2,13 | 2,06 | 1,97 | 1,93 | 1,88 | 1,84 | 1,79 | 1,73 | 1,67 | |
| 2,19 | 2,12 | 2,04 | 1,96 | 1,91 | 1,87 | 1,82 | 1,77 | 1,71 | 1,65 | |
| 2,18 | 2,10 | 2,03 | 1,94 | 1,90 | 1,85 | 1,81 | 1,75 | 1,70 | 1,64 | |
| 2,16 | 2,09 | 2,01 | 1,93 | 1,89 | 1,84 | 1,79 | 1,74 | 1,68 | 1,62 | |
| 2,08 | 2,00 | 1,92 | 1,84 | 1,79 | 1,74 | 1,69 | 1,64 | 1,58 | 1,51 | |
| 1,99 | 1,92 | 1,84 | 1,75 | 1,70 | 1,65 | 1,59 | 1,53 | 1,47 | 1,39 | |
| 1,91 | 1,83 | 1,75 | 1,66 | 1,61 | 1,55 | 1,50 | 1,43 | 1,35 | 1,25 | |
| ¥ | 1,83 | 1,75 | 1,67 | 1,57 | 1,52 | 1,46 | 1,39 | 1,32 | 1,22 | 1,00 |
Таблица 5.
Доверительные интервалы для неизвестных параметров
Нормальных распределений
| № п/п | Параметр | Информация о других параметрах распределения | Доверительный интервал параметра с доверительной вероятностью g |
| 1. | mX | sX известно | 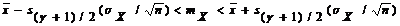 |
| 2. | mX | sX неизвестно | 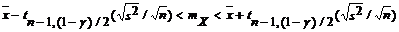 |
| 3. | s2X | mX известно | 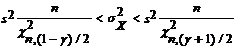 |
| 4. | s2X | mX неизвестно | 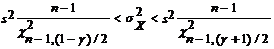 |
| 5. | sX | mX неизвестно | 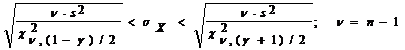 |
| 6. | 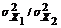 | 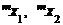 неизвестны неизвестны | 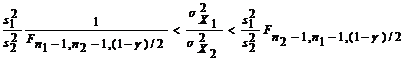 |
| 7. | r | 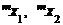 и и 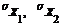 неизвестны неизвестны | 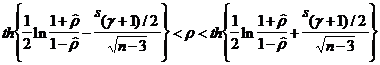 это справедливо для достаточно больших n (n > 10) это справедливо для достаточно больших n (n > 10) |
____________
Примечание:
| n - | объем выборки x1, x2, ... xn; | |
| sp - | квантиль уровня p нормированного нормального распределения; | (см. таблицу 1) |
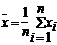 - - | выборочное среднее; | |
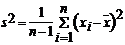 - - | выборочное значение дисперсии СВ X; | |
| r - | коэффициент корреляции СВ X1 и X2; | |
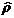 - - | выборочный коэффициент корреляции СВ X1 и X2; | |
| c2n, a - | значение распределения Пирсона; | (см. таблицу 2) |
| tn, a - | значение t - распределения Стьюдента; | (см. таблицу 3) |
| Fn1,n2, a - | значение F - распределения Фишера. | (см. таблицу 4) |
