Обучающиеся и игровые системы.

Обучающиеся системы

Обучающиеся системы (ОС) являются одним из самых сложных и пока малоизученных классов адаптивных систем. Их сложность следует хотя бы из того, что они должны имитировать деятельность живого организма, причем высшую деятельность. Не стоит, может быть, говорить об имитации сознательной, разумной деятельности, хотя, во-первых, в обучении человека и животного много общего, во-вторых, современные обучающиеся системы, например шахматные компьютеры, вернее их программы, пытаются моделировать именно сознательную деятельность.

ОС создаются на основе принципа обучения, заключающемся в последовательном накапливании опыта формирования поведения системы при высокой степени неопределенности ее исходных состояний, по результатам которого происходит улучшение функционирования системы. Характер накопления опыта при обучении весьма многообразен, например, опыт может быть положительным и отрицательным, систематизированным и случайным, собственным или привнесенным извне, искусственным или естественным и т.д. Однако у всех способов накопления опыта есть общая черта – постепенное выделение «области знаний» из всей совокупности «незнания». Поэтому в теории обучающихся систем эта особенность нашла отражение в достаточно быстро развивающемся направлении, связанном с созданием автоматических систем классификации и распознавания образов. Под распознаванием здесь понимается установление по результатам накопленного опыта границ между определенными классами сложных ситуаций. Задачи распознавания и классификации встречаются часто не только в технических приложениях, но и в таких областях как медицинская диагностика, геологическая разведка месторождений, прогнозирование погоды и т.д.

Задача автоматического обучения распознаванию образов формулируется следующим образом: каждой возможной ситуации из множества рассматриваемых ставится в соответствие точка некоторого пространства 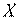информационных признаков. Заранее известно, что в пространстве 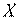необходимо выделить две или большее число областей или классов ситуаций. Расположение границ между областями неизвестно и нет определенных правил, по которым можно определить принадлежность той или иной точки заданных областей. Цель обучения заключается в построении поверхности, разделяющей предъявляемые точки из указанного множества на заданное число классов. Существуют два подхода к обучению

Обучение с поощрением.Классифицирующему автомату предъявляется ряд точек из множества в пространстве 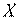и сообщается информация о принадлежности этих точек определенным классам. После определенного цикла обучения на таких примерах автомат строит разделяющую поверхность и может в дальнейшем отличать принадлежность разным классам не только точек-примеров, но и любых других точек в пространстве .

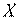Обучение без поощоения.В случае информации о принадлежности точек разделяемым классам отсутствует. Автомат по наблюдению предъявляемых точек определяет факт компактного расположения некоторых из них и затем строит разделяющие поверхности на основе выбранной меры близости компактных групп точек к разделяющей поверхности.

Объективная сложность обучения как с поощрением так и без заключается в том, что не всегда классы из близко расположенных друг к другу точек строго отделены, т.е. возможны пересечения классов, когда одни и те же точки принадлежат разным классам. Часто сами классы сформулированы нечетко и и даже человек иногда затрудняется при классификации, не то что машина.

Для хорошо разделимых классов используют достаточно простые алгоритмы автоматической классификации, основанные на аппроксимации разделяющих поверхностей отдельными участками гиперплоскостей. Для менее разделимых классов приходится использовать вероятностные методы характеристик принадлежности точек пересекающимся классам.

Одним из таких методов является метод секущих плоскостей. Пусть требуется разделить три фигуры, состоящие из набора точек. Точки появляются по порядку. Линия 1 разделяет точки 1 и 2, принадлежащие разным фигурам. Линия 2 устраняет противоречие, связанное с появление точки 3. Появление точек 4,5 не вносит противоречий, но с появлением точки 6 ее нужно отделить от 4,5, что делается линией 3. Линия 4 отделяет точку 6 от новой точки 7. Окончательно гиперплоскость формируется отрезками гиперплоскостей.

Игровые системы

Игровые системы (ИС) используются для управления различного рода операциями, представляющими в своей основе игру против организованного противника (военные операции, игры) или сил природы (случайного процесса).

Структурная схема игровой системы приведена на рис. 5.1. В системе всегда рассматривается действие двух сторон. Игровой алгоритм заключается в сравнении возможных в данной обстановке решений и выборе из большого их числа оптимального.

Сравнение вариантов делается управляющей машиной на основе заложенных в нее критериев. Эти критерии выражаются в виде функции выгоды. Установление рациональной функции выгоды представляет основную проблему при построении игровых систем. Этими проблемами занимается математическая дисциплина – теория игр. Главным ее содержанием является обоснование так называемых оптимальных стратегий игры. Наиболее полно теория игр разработана для конечных игр, для которых характерно конечное число ходов (вариантов) и, следовательно, конечное число возможных стратегий.

В настоящее время используются игровые алгоритмы двух видов.

● С набором шаблонных решений. Все решения заранее исследуются и нумеруются. Задачей является выбор решения, которое дает максимум функции выгоды. Недостаток подхода – малая гибкость и приспособляемость ИС.

● С использованием принципа динамического программирования. Задача решается по отдельным этапам. Результат выполнения команд управления на предыдущем шаге является исходным для формирования команд управления на следующем шаге.

Типовыми задачами, решаемыми ИС, являются:

● Задача преследования одного управляемого объекта другим,

● Задача приведения управляемого объекта в некоторое заданное состояние при действии неизвестных возмущений.

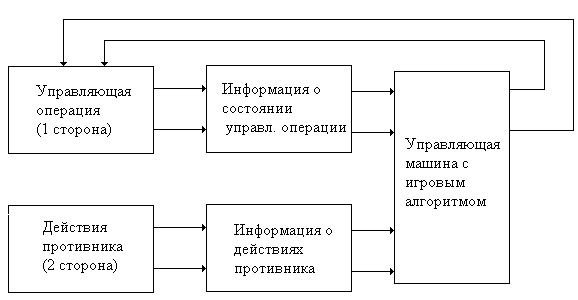
Рис.5.1. Структура игровой системы

Сутью игровой задачи является конфликтная ситуация. Пусть два партнера могут управлять процессами в некоторой динамической системе, описываемой дифференциальными уравнениями

,

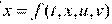где 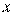- полный вектор состояния,

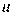- управление 1-го игрока,

- управление 2-го игрока.

Игра начинается в момент 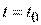и считается законченной при 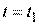, когда 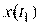попадает в заданную область. Задача первого игрока – закончить игру с минимальным значением показателя качества (плата за игру)

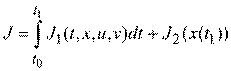
где 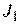и 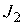- известные функции.

Задача второго игрока – помешать приведению точки в заданную область или, по крайней мере, увеличить 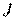. Обычно задача решается в условиях ограничений на уровни управляющих воздействий .

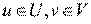Пусть 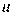и - допустимые стратегии, которые могут выбирать игроки. Если первый игрок выбрал стратегию 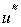, то наихудший результат для него будет при выборе вторым игроком стратегии 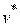, максимизирующей плату за игру

.

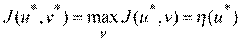Естественно, что первый игрок будет искать такую стратегию 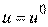при которой 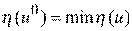для всех допустимых стратегий. Условие выбора можно записать

.

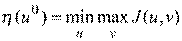Для второго игрока найти оптимальную максиминную стратегию 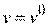из условия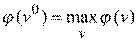

В этом случае второй игрок обеспечит себе выигрыш не менее

.

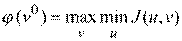Первый игрок не может иметь гарантии, что его проигрыш будет меньше, чем минимальный выигрыш 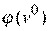, который гарантируется второму игроку. Поэтому .

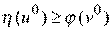В случае равенства 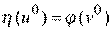возникает седловая точка игры, при которой

,

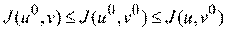а также

.

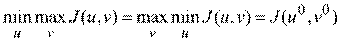Оптимальные стратегии 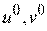соответствующие седловой точке игры, определяют для каждого игрока наилучший способ действий. Отклонение от оптимальной стратегии любого из игроков (если другой придерживается своей оптимальной стратегии) может только ухудшить результат.

СПИСОК ЛИТЕРАТУРЫ

1. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. – М.: Наука, 1986.

2. Куропаткин П.В.. Оптимальные и адаптивные системы : учебное пособие / П. В. Куропаткин. — М. : Высшая школа, 1980. — 287 с.

3. Александров А.Г.. Оптимальные и адаптивные системы : учебное пособие / А. Г. Александров. — М. : Высшая школа, 1989. — 262 с.

4. Чураков Е.П.. Оптимальные и адаптивные системы : учебное пособие / Е. П. Чураков. — М. : Энергоатомиздат, 1987. — 254 с.

5. Вадутов О.С.. Адаптивные системы автоматического управления : учебное пособие / О. С. Вадутов ; Томский политехнический институт. — Томск : Изд-во ТПИ, 1991. — 95 с.

6. Красовский А.А. справочник по ТАУ

Учебное издание

ВОРОНИН Александр Васильевич