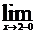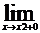Непрерывность функции в точке. Точки разрыва
Функция f(x) называется непрерывной в точке х0, если при х → х0 предел функции существует и равен ее частному значению в этой точке, т.е.
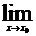 f(x) = f(x0).
f(x) = f(x0).
Для непрерывности функции f(x) в точке х0 необходимо и достаточно выполнение следующих условий:
1) функция должна быть определена точке х0 и в некоторой окрестности, содержащей эту точку;
2) функция должна иметь равные односторонние пределы
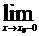 f(x) =
f(x) = 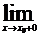 f(x);
f(x);
3) односторонние пределы функции при х → х0 равны значению функции в этой точке 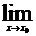 f(x) = f(x0).
f(x) = f(x0).
Функция f(x) называется разрывной в точке х0, если она определена в сколь угодно близких точках, но в самой точке х0 не удовлетворяет хотя бы одному из условий непрерывности.
Разрыв функции f(x) в точке х0, называется конечным, или 1-го рода, если существуют конечные односторонние пределы 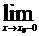 f(x) и
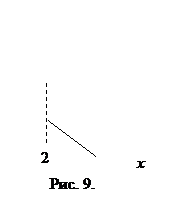
f(x) и 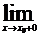 f(x). Функция f(x), график которой приведен на рисунке 9, имеет в точке х = 2 разрыв первого рода, так как для нее существуют пределы при х → 2 справа и слева.
f(x). Функция f(x), график которой приведен на рисунке 9, имеет в точке х = 2 разрыв первого рода, так как для нее существуют пределы при х → 2 справа и слева.

Точка разрыва, не являющаяся точкой разрыва первого рода, называется точкой разрыва второго рода. Функция у = 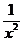 , график которой приведен на рисунке 10, имеет в точке х = 0 разрыв второго рода, так как при х → 0 для нее не существует предела ни слева, ни справа.
, график которой приведен на рисунке 10, имеет в точке х = 0 разрыв второго рода, так как при х → 0 для нее не существует предела ни слева, ни справа.
Скачком функции f(x) в точке разрыва х0, называется разность ее односторонних пределов 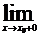 f(x) –
f(x) – 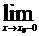 f(x) если они различны.
f(x) если они различны.
Пример. Дана функция у =  . Найти ее точки разрыва, если они существуют и скачок функции в каждой точке разрыва.
. Найти ее точки разрыва, если они существуют и скачок функции в каждой точке разрыва.
Решение.
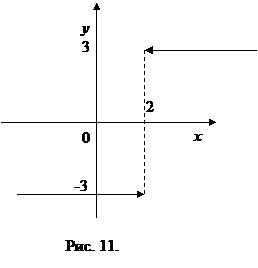
Функция у =  определена и непрерывна на всей числовой прямой, кроме точки х = 2. Из этого следует что в точке х = 2 функция имеет разрыв (рис. 11.).
определена и непрерывна на всей числовой прямой, кроме точки х = 2. Из этого следует что в точке х = 2 функция имеет разрыв (рис. 11.).
| |||
 | |||
٭ ٭
٭
٭ ٭
٭
150. Исходя из определения, доказать непрерывность функций:
а) у = х2 + х – 2 для всех х 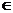 (- ∞; + ∞);
(- ∞; + ∞);
b) у = х3 – 2х +4 для всех х 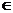 (- ∞; + ∞).
(- ∞; + ∞).
151. Исходя из определения, доказать непрерывность функций:
а) у = sin (3x + 2) для всех х 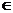 (- ∞; + ∞);
(- ∞; + ∞);
b) у = cos (5x – 1) для всех х 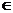 (- ∞; + ∞).
(- ∞; + ∞).
152. Исследовать функции на непрерывность, установить род точек разрыва:
а) у = х +  ; ; | d) у =  ; ; |
b) у = 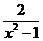 ; ; | е) у =  ; ; |
с) у = е  ; ; | f) у = tg 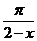 . . |
153. Исследовать функции на непрерывность, установить род точек разрыва:
 х2 при - ∞ < х < 1, 2х- 1 при 1≤ х < ∞; х2 при - ∞ < х < 1, 2х- 1 при 1≤ х < ∞; |  cos cos  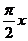 при - ∞ < х < 1, х – 1 при 1≤ х < ∞; при - ∞ < х < 1, х – 1 при 1≤ х < ∞; | ||
| а) у = | с) у = | ||
 | -  при х < 0, 1 при 0 ≤ х < 1, х при 1 ≤ х ≤ 2 ; при х < 0, 1 при 0 ≤ х < 1, х при 1 ≤ х ≤ 2 ; | 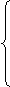 . . |  при х < 0, при х < 0, |
| b) у = | d) у = | х при 1 ≤ х < 2, | |
| 3 при 2 ≤ х ≤ 3. |
154. Найти точки разрыва функции, если они существуют, и скачок функции в каждой точке разрыва:
а) у = х +  ; ; | с) у =  ; ; |
b) у = 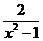 ; ; | d) у =  . . |
155. Найти точки разрыва функции, если они существуют, и скачок функции в каждой точке разрыва:
а) у = 4х –  ; ; | с) у = 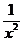 ; ; |
b) у = 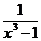 ; ; | d) у = 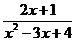 . . |
156. Найти точки разрыва функции, если они существуют, скачок функции в каждой точке разрыва и построить график:
а) у = 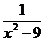 ; ; | с) у = 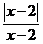 ; ; |
b) у = 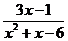 ; ; | d) у = arcctg  . . |
157. Найти точки разрыва функции, если они существуют, скачок функции в каждой точке разрыва и построить график:
| а) у = | 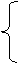 - - 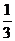 х2 при х ≤ 3, х2 при х ≤ 3, |
| х при х > 3; | |
| b) у = | 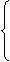 3 3 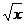 при 0 ≤ х ≤ 1, при 0 ≤ х ≤ 1, |
| 7 - 3х при 1< х < 4, | |
2х +1 при 4 ≤ х < + ∞;  | |
| с) у = | 3х -1 при - ∞ < х < - 1, |
 при - 1≤ х < ∞. при - 1≤ х < ∞. |
Глава 4. Дифференциальное исчисление функций одной переменной
§1.Производная функции