Урновая схема: выбор без возвращения, с учетом порядка
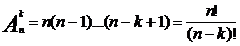 |
Общее количество выборок в схеме выбора k элементов из n без возвращения и с учетом порядка определяется числом размещений из n элементов по k элементов.
Урновая схема: выбор без возвращения и без учета порядка
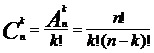 |
Общее количество выборок в схеме выбора k элементов из n без возвращения и без учета порядка определяется числом сочетаний из n элементов по k элементов:
Урновая схема: выбор с возвращением и с учетом порядка
Общее количество выборок в схеме выбора k элементов из n с возвращением и с учетом порядка определяется числом перестановок из  элементов:
элементов:
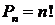
Урновая схема: выбор с возвращением и без учета порядка
Рассмотрим урну с двумя шариками и перечислим результаты выбора двух шариков из этой урны при выборе с возвращением:
| С учетом порядка | Без учета порядка |
| (1, 1) (2, 2) (1, 2) (2, 1) | (1, 1) (2, 2) (1, 2) |
В схеме «без учета порядка» получилось 3 различных результата в отличие от четырех в схеме «с учетом порядка». Тогда общее количество выборок в схеме выбора k элементов из n с возвращением и без учета порядка определяется числом сочетаний с повторениями
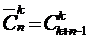 .
.
Заметим, что число выборок, различающихся еще и порядком, в k! раз больше, чем число выборок, различающихся только составом.
Пример. Рассмотрим выбор двух шариков из двух или, что то же самое, дважды подбросим монету. Если учитывать порядок, то исходов получится 4, и все они равновозможны, то есть имеют вероятность по 1/4:
(герб, герб), (решка, решка), (решка, герб), (герб, решка).
Если порядок не учитывать, то два последних исхода будут с одним и тем же результатом эксперимента, и получим три исхода вместо четырех: выпало два герба, либо две решки, либо один герб и одна решка.
При этом первые два исхода имеют вероятность 1/4, а последний — вероятность 1/4+1/4=1/2.
Геометрическая вероятность
Рассмотрим какую-нибудь область 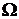 на прямой, на плоскости, в пространстве. Предположим, что «мера»
на прямой, на плоскости, в пространстве. Предположим, что «мера» 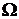 (длина, площадь, объем, соответственно) конечна. Пусть случайный эксперимент состоит в том, что мы наудачу бросаем в эту область точку а. Термин «наудачу» здесь означает, что вероятность попадания точки в любую часть
(длина, площадь, объем, соответственно) конечна. Пусть случайный эксперимент состоит в том, что мы наудачу бросаем в эту область точку а. Термин «наудачу» здесь означает, что вероятность попадания точки в любую часть 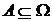 не зависит от формы или расположения области
не зависит от формы или расположения области 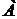 внутри области
внутри области 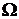 , а зависит лишь от «меры» области.
, а зависит лишь от «меры» области.
Эксперимент удовлетворяет условиям «геометрического определения вероятности», если его исходы можно изобразить точками некоторой области 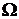 так, что вероятность попадания точки в любую
так, что вероятность попадания точки в любую 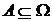 не зависит от формы или расположения
не зависит от формы или расположения 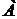 внутри
внутри 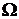 , а зависит лишь от меры
, а зависит лишь от меры 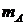 области
области 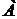 (и, следовательно, пропорциональна этой мере).
(и, следовательно, пропорциональна этой мере).
«Мерой» 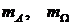 будем называть длину, площадь, объем и т.д. Тогда вероятность будет равна:
будем называть длину, площадь, объем и т.д. Тогда вероятность будет равна:
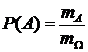 .
.
Частные случаи геометрической вероятности.
1. Пусть 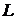 – длина отрезка, содержащего в себе все элементарные исходы,
– длина отрезка, содержащего в себе все элементарные исходы, 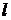 – длина части отрезка. Пусть на отрезок наудачу поставлена точка, и верны следующие предположения:
– длина части отрезка. Пусть на отрезок наудачу поставлена точка, и верны следующие предположения:
а) поставленная точка может оказаться в любой точке отрезка 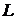 (все исходы равновозможны);
(все исходы равновозможны);
б) вероятность попадания точки на отрезок 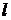 пропорциональна длине этого отрезка и не зависит от его расположения относительно
пропорциональна длине этого отрезка и не зависит от его расположения относительно 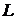 .
.
Тогда вероятность попадания точки на отрезок 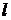 будет равна отношению длин отрезков:
будет равна отношению длин отрезков:
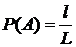 .
.
2. Пусть 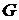 – плоская фигура, включающая в себя все элементарные исходы,
– плоская фигура, включающая в себя все элементарные исходы, 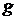 – часть фигуры
– часть фигуры 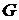 . На фигуру
. На фигуру 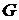 брошена точка и верны следующие предположения:
брошена точка и верны следующие предположения:
а) поставленная точка может оказаться в любой точке фигуры 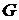 (все исходы равновозможны);
(все исходы равновозможны);
б) вероятность попадания точки на фигуру 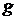 пропорциональна площади этой фигуры и не зависит от ее расположения относительно
пропорциональна площади этой фигуры и не зависит от ее расположения относительно 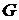 .
.
Тогда вероятность попадания точки в область 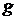 будет равна отношению площадей фигур:
будет равна отношению площадей фигур:
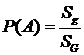 .
.
3. Аналогично вводиться вероятность, если 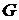 - пространственная фигура, тогда вероятность попадания точки на фигуру
- пространственная фигура, тогда вероятность попадания точки на фигуру 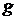 будет равна отношению объемов фигур:
будет равна отношению объемов фигур:
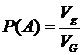 .
.
Замечание.
1. В случае классического определения вероятности вероятность достоверного события равна 1, вероятность невозможного события равна 0; справедливо и обратное утверждение: если вероятность равна 0, то событие невозможно.
2. В случае геометрической вероятности обратное утверждение не справедливо, например, вероятность попадания брошенной точки в определенную точку области равна 0, но это событие может произойти, следовательно, не является невозможным.
Пример. На плоскости начерчены две концентрические окружности с радиусами 5 и 10 см. найти вероятность того, что точка, брошенная наугад в большой круг, попадет также в кольцо образованное построенными окружностями?
Решение.
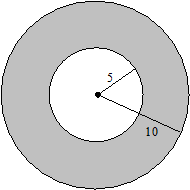 | Событие 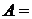 {точка попадет в кольцо}. Общее число исходов, то есть площадь фигуры, в которую может попасть точка в данном опыте, есть площадь большей окружности: {точка попадет в кольцо}. Общее число исходов, то есть площадь фигуры, в которую может попасть точка в данном опыте, есть площадь большей окружности: 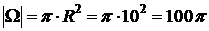 . Число исходов, удовлетворяющих событию . Число исходов, удовлетворяющих событию 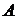 , есть площадь кольца, образованного двумя окружностями: , есть площадь кольца, образованного двумя окружностями: |
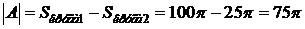 .
.
Тогда искомая вероятность:
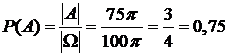 .
.
Пример. Точка наудачу бросается на отрезок [0,1]. Вероятность точке попасть в точку {0.5} равна нулю, так как мера множества, состоящего из одной точки («длина точки»), равна 0. Вместе с тем попадание в точку {0.5} не является невозможным событием — это один из элементарных исходов эксперимента.
