Криволинейное движение. Нормальное и тангенсальное ускорения.
Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек.
Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. В случае криволинейного движения с постоянным ускорением в плоскости XOY проекции vx и vy ее скорости на оси Ox и Oy и координаты x и y точки в любой момент времени t определяется по формулам:
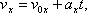
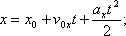
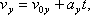
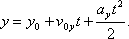
Частным случаем криволинейного движения – является движение по окружности. Движение по окружности, даже равномерное, всегда есть движение ускоренное: модуль скорости все время направлен по касательной к траектории, постоянно меняет направление, поэтому движение по окружности всегда происходит с центростремительным ускорением.
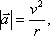где r – радиус окружности.
Вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости.
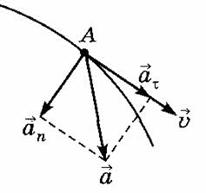
При криволинейном движении ускорение можно представить как сумму нормальной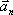 
и тангенциальной 
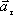составляющих:
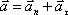
- нормальное (центростремительное) ускорение, направлено к центру кривизны траектории и характеризует изменение скорости по направлению:
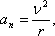
v – мгновенное значение скорости, r – радиус кривизны траектории в данной точке.
- тангенциальное (касательное) ускорение, направлено по касательной к траектории и характеризует изменение скорости по модулю.
Полное ускорение, с которым движется материальная точка, равно:
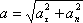
Первый закон Ньютона. Принцип относительности Галилея.
Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Стремление тела сохранять состояние
покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют также законом инерции. Механическое движение относительно, и его характер зависит от системы отсчета. Первый закон Ньютона
выполняется не во всякой системе отсчета, а те системы, по отношению к которым он выполняется, называются инерциальными системами отсчета. Инерциальной системой отсчета является такая система отсчета, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется равномерно и
прямолинейно. Первый закон Ньютона утверждает существование инерциалъных систем отсчета.
Масса и импульс тела. Закон сохранения импульса. Второй закон Ньютона.
Импульс.
В ньютоновской механике масса материальной точки не зависит от времени 
, а ускорение 
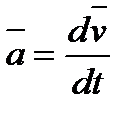, где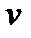 
- скорость точки. Поэтому можно записать:
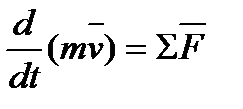- II закон Ньютона в дифференциальной форме.
или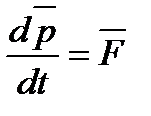 
Вектор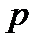 
, равный произведению массы материальной точки на ее скорость, называется импульсом материальной точки.
Скорость изменения импульса тела пропорциональна силе, действующей на тело.
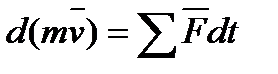, (где 
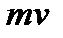-импульс тела, 
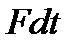- импульс силы).
Масса тела — физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные {инертная масса) и гравитационные {гравитационная масса) свойства. В настоящее время можно считать доказанным, что инертная и гравитационная массы равны друг другу (с точностью, не меньшей 10~12 их
значения).
Закон сохранения импульса.Импульс изолированной или замкнутой системы 2-х материальных точек сохраняется, т. е. остаёьтся неизменным во времени, каково бы ни было взаимодействие между нимим. Это утверждение справедливо также и для изолированной с. м. т., состоящей из сколь угодно большого числа м. т.
Запишем третий закон Ньютона для замкнутой системы, состоящей из произвольного числа материальных точек.
F1(i)+F2(i)+…+Fn(i)=0, (1)
где Fn(i) – полная внутренняя сила., действующая на n-ную точку. Обозначим далее символами F1(e),F2(e),… внешние силы , действующие на материальные точки системы. Тогда на основании второго закона Ньютона можно записать
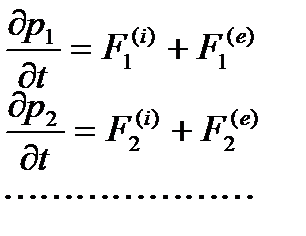
Сложив почленно эти уравнения и приняв во внимание соотношение (1) найдем
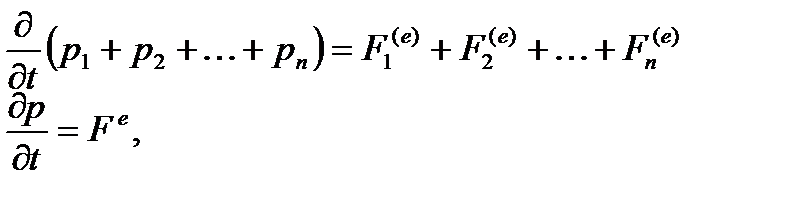(2)
где р- импульс всей системы,F(e)-равнодействующая всех внешних сил, действующая на нее. Пусть теперь геометрическая сумма всех внешних сил равна нулю (Например замкнутая система). Тогда (dp/dt)=0, или p=const.
Закон сохранения импульса является отражением фундаментального св-ва пространства - его однородности.