Кинематические уравнения движения материальной точки

Кинематические уравнения движения материальной точки

В общем случае ее движение определяется скалярными уравнениями x=x(t), y=y(t),z=z{t)

векторному уравнению r = r(t).

В декартовой системе координат, используемой наиболее часто, положение точки А в данный момент времени по отношению к этой системе характеризуется тремя координатами х, у и z или радиусом-вектором г, проведенным из начала системы координат в данную точку

Движение материальной точки будет описано полностью, если известно ее положение в любой момент времени относительно выбранной системы отсчета. Полное описание движения сводится к нахождению трех координат: x = x(t); y = y(t); z = z(t); или к нахождению векторной функции r = r(t)

Число независимых величин, полностью определяющих положение точки в пространстве, называется числом степеней свободы.

Траектория — линия, описываемая в пространстве движущейся точкой

2)Путь, перемещение, скорость, ускорение.

Длина участка траектории А В, пройденного материальной точкой смомента начала отсчета времени, называется длиной пути (дельта)S является скалярной функцией времени: As = As(t).

Вектор (дельта)г = г2 — Г1 проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени), называется перемещением.

Скорость –векторная величина, быстрота движения.

Скорость- векторная физическая величина, служащая для характеристики направления и быстроты движения точки в механике. Средней скоростью точки в промежутке времени от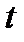

до 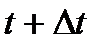называется вектор 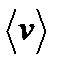, равный отношению приращения 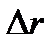радиуса-вектора точки за этот промежуток времени к его продолжительности :

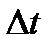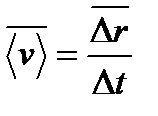
Средняя скорость направлена так же, как вектор перемещения 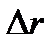, то есть вдоль хорды, стягивающей соответствующий участок траектории точки.

Скоростью точки в момент времени 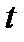называется вектор 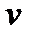, равный первой производной по времени от радиуса-вектора этой точки:

.

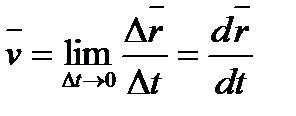
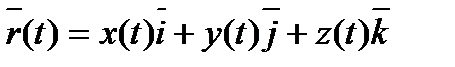Вектор 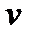можно разложить по базису 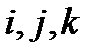, то есть на три составляющие по осям прямоугольной декартовой системы координат.

.

.

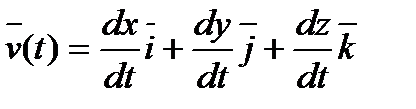
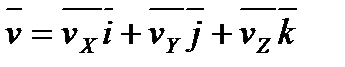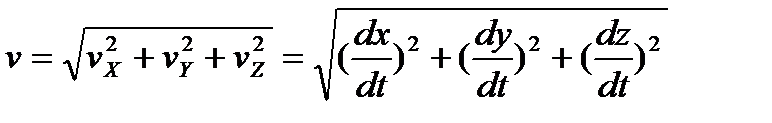Вектором средней скорости (v) называется отношение приращения (дельта)градиуса-вектора точки к промежуткувремени At:

Направление вектора средней скорости совпадает с направлением (дельта)г. При неограниченном уменьшении At средняя скорость стремится к предельному значению, которое называется мгновенной скоростью v:

Ускорение – это величина, показывающая, как изменяется скорость за одну секунду.

Ускорение.

Ускорение- векторная физическая величина, характеризующая быстроту изменения скорости .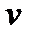

Ускорением называется вектор 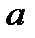, равный первой производной по времени 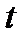от скорости 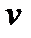этой точки. Ускорение точки также равно второй производной по времени от радиуса-вектора 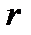этой точки:

.

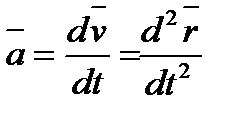Разложение ускорения точки по базису 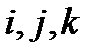, то есть на составляющие по осям прямоугольной декартовой системы координат, имеет вид:

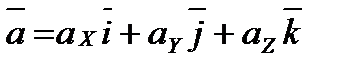, где

, , .

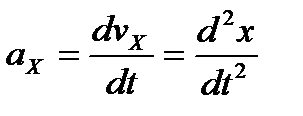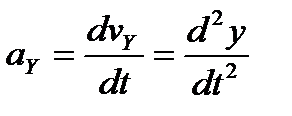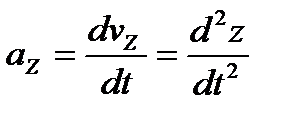Здесь 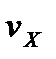, , 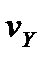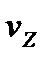- компоненты скорости точки, а 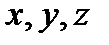- координаты точки в рассматриваемый момент времени.

За единицу скорости принимают скорость такого равномерного прямолинейного движения, при котором тело за одну секунду перемещается на один метр.

Ускорение – это величина, показывающая, как изменяется скорость за одну секунду.

Импульс.

В ньютоновской механике масса материальной точки не зависит от времени 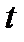, а ускорени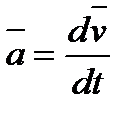е , где 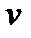- скорость точки. Поэтому можно записать:

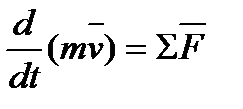- II закон Ньютона в дифференциальной форме.

или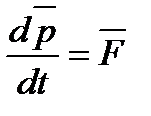

Вектор 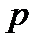, равный произведению массы материальной точки на ее скорость, называется импульсом материальной точки.

Скорость изменения импульса тела пропорциональна силе, действующей на тело.

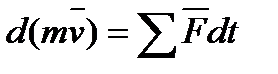, (где 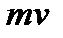-импульс тела, 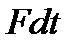- импульс силы).

Масса тела — физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные {инертная масса) и гравитационные {гравитационная масса) свойства. В настоящее время можно считать доказанным, что инертная и гравитационная массы равны друг другу (с точностью, не меньшей 10~12 их

значения).

Закон сохранения импульса.Импульс изолированной или замкнутой системы 2-х материальных точек сохраняется, т. е. остаёьтся неизменным во времени, каково бы ни было взаимодействие между нимим. Это утверждение справедливо также и для изолированной с. м. т., состоящей из сколь угодно большого числа м. т.

Запишем третий закон Ньютона для замкнутой системы, состоящей из произвольного числа материальных точек.

F₁⁽ⁱ⁾+F₂⁽ⁱ⁾+…+Fn⁽ⁱ⁾=0, (1)

где Fn⁽ⁱ⁾ – полная внутренняя сила., действующая на n-ную точку. Обозначим далее символами F₁^(e),F₂^(e),… внешние силы , действующие на материальные точки системы. Тогда на основании второго закона Ньютона можно записать

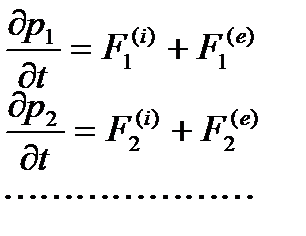
Сложив почленно эти уравнения и приняв во внимание соотношение (1) найдем

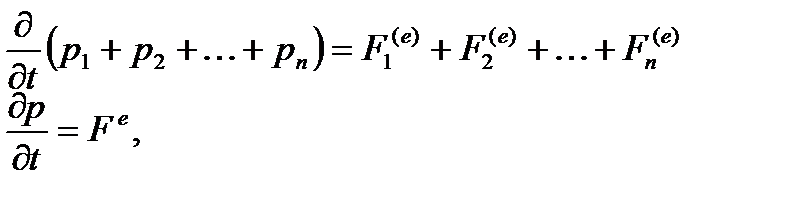(2)

где р- импульс всей системы,F^(e)-равнодействующая всех внешних сил, действующая на нее. Пусть теперь геометрическая сумма всех внешних сил равна нулю (Например замкнутая система). Тогда (dp/dt)=0, или p=const.

Закон сохранения импульса является отражением фундаментального св-ва пространства - его однородности.

Упругие силы. Закон Гука.

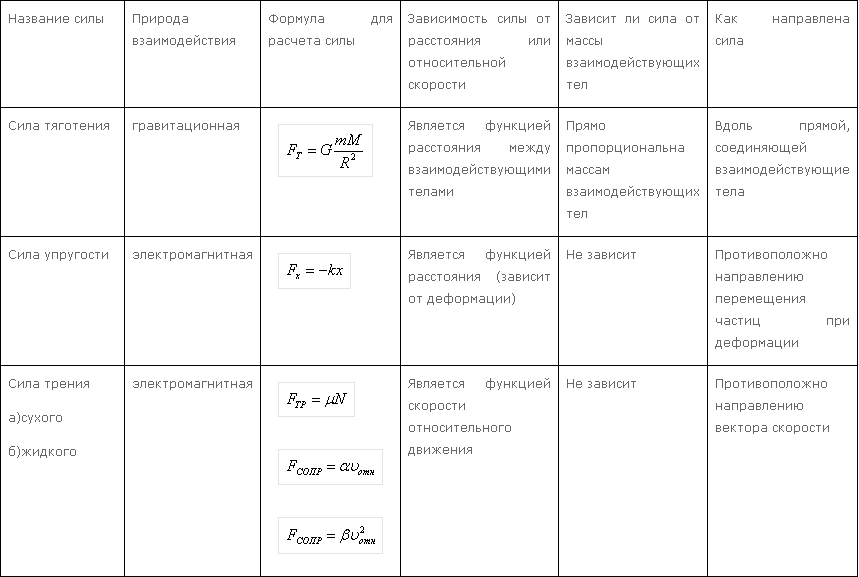
Си́ла упру́гости — сила, возникающая при деформации тела и противодействующая этой деформации.

В случае упругих деформаций является потенциальной. Сила упругости имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. В простейшем случае растяжения/сжатия тела сила упругости направлена противоположно смещению частиц тела, перпендикулярно поверхности.

Вектор силы противоположен направлению деформации тела (смещению его молекул

Электромагнитные силы в механике проявляют себя как упругие силы и силы трения.

Под действием внешних сил возникают деформации (т.е. изменение размеров и формы) тел. Если после прекращения действия внешних сил восстанавливаются прежние форма и размеры тела, то деформация называется упругой. Деформация имеет упругий характер в случае, если внешняя сила не превосходит определенного значения, называемого пределом упругости.

При превышении этого предела деформация становится пластичной, или неупругой, т.е. первоначальные размеры и форма тела полностью не восстанавливаются.

Рассмотрим упругие деформации. В деформированном теле (рис. 4.2) возникают упругие силы, уравновешивающие внешние силы. Под действием внешней силы – Fвн пружина получает удлинение x, в результате в ней возникает упругая сила – Fупр, уравновешивающая Fвн.

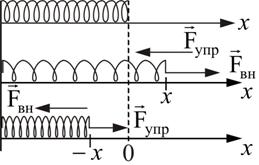
Рис. 4.2 Упругие силы возникают во всей деформированной пружине. Любая часть пружины действует на другую часть с силой упругости Fупр.

Удлинение пружины пропорционально внешней силе и определяется законом Гука: (4.3.1) х = F_вн * 1/k

k – жесткость пружины. Видно, что чем больше k, тем меньшее удлинение получит пружина под действием данной силы.

Так как упругая сила отличается от внешней только знаком, т.е. Fупр = –Fвн, закон Гука можно записать в виде

Закон Гука: Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации.

х = - F_упр * 1/k

Fупр = –kx.

Потенциальная энергия.

Потенциальная энергия — скалярная физическая величина, характеризующая способность некоего тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы[1]. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.

Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.

Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными.

Вращательное

движение — это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.

Затухающие колебания.

Сложение колебаний

Рассмотрим вращающийся против часовой стрелки с постоянной угловой скоростью w вектор А. Очевидно, что угол j = wt + j0 где j0 - начальный угол.

Проекции вектора А на оси координат запишутся:

Видно, что проекции вращающегося вектора на оси координат по форме совпадают с уравнением гармонических колебаний, если угловой скорости вектора сопоставить угловую частоту колебаний, а начальному углу - начальную фазу.

Проводя аналогию дальше, можно сказать, что результат сложения двух однонаправленных колебаний можно получить следующим путем: необходимо сложить два вектора, а проекции суммарного вектора на оси координат будут являться уравнениями результирующего колебания. Рассмотрим этот метод на примере сложения двух колебаний с произвольными частотами. Пусть наше тело участвует в двух совпадающих по направлению колебаниях:

Сопоставим этим колебаниям два вектора А1 и А2, вращающихся с соответствующими угловыми скоростями.

Сопоставляем колебаниям проекции векторов на ось y. Задача сложения колебаний сводится к нахождению проекции вектора А на ось y (амплитуда результирующего колебания) и угла f (фаза результирующего колебания).

Из очевидных геометрических соображений находим:

Отметим, что в общем случае сложения колебаний с разными частотами амплитуда результирующего колебания будет зависеть от времени. Если же частоты одинаковы, то , то есть зависимость от времени исчезает. На языке векторной диаграммы это означает, что складываемые векторы при своем вращении не меняют своего относительного положения. В этом случае формулы для амплитуды и фазы результирующего колебания запишутся так:

Рассмотрим сложение двух однонаправленных колебаний с неравными, но близкими частотами, то есть, и пусть для определенности . Для простоты пусть начальные фазы и амплитуды этих колебаний равны. В результате сложения двух колебаний

получим уравнение суммарного колебания:

Полученное результирующее колебание не является гармоническим (сравни с уравнением (1)); такого вида колебания носят название биений, название понятно, если посмотреть на график колебаний.

Величина, стоящая перед синусом, меняется со временем относительно медленно, так как разность частот мала. Эту величину условно называют амплитудой биений, а разность складываемых частот - частотой биений (циклической).

При сложении взаимно перпендикулярных колебаний необходимо найти уравнение траектории тела, то есть из уравнений колебаний типа x = x(t), y = y(t) исключить t и получить зависимость типа y(x).

например, сложим два колебания с одинаковыми частотами:

исключив время, получим:

В общем случае это - уравнение эллипса. При A1=A2 - окружность, при (m - целое) - отрезок прямой.

Вид траектории при сложении взаимно перпендикулярных колебаний зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Получающиеся кривые носят название фигур Лиссажу.

Цикл Карно

Энтропия

Закон термодинамики

Поверхностное натяжение.

Смачивание

Уравнение Бернулли.

Диффузия

Вязкость

Теплопроводность

Кинематические уравнения движения материальной точки

В общем случае ее движение определяется скалярными уравнениями x=x(t), y=y(t),z=z{t)

векторному уравнению r = r(t).

В декартовой системе координат, используемой наиболее часто, положение точки А в данный момент времени по отношению к этой системе характеризуется тремя координатами х, у и z или радиусом-вектором г, проведенным из начала системы координат в данную точку

Движение материальной точки будет описано полностью, если известно ее положение в любой момент времени относительно выбранной системы отсчета. Полное описание движения сводится к нахождению трех координат: x = x(t); y = y(t); z = z(t); или к нахождению векторной функции r = r(t)

Число независимых величин, полностью определяющих положение точки в пространстве, называется числом степеней свободы.

Траектория — линия, описываемая в пространстве движущейся точкой

2)Путь, перемещение, скорость, ускорение.

Длина участка траектории А В, пройденного материальной точкой смомента начала отсчета времени, называется длиной пути (дельта)S является скалярной функцией времени: As = As(t).

Вектор (дельта)г = г2 — Г1 проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени), называется перемещением.

Скорость –векторная величина, быстрота движения.

Скорость- векторная физическая величина, служащая для характеристики направления и быстроты движения точки в механике. Средней скоростью точки в промежутке времени от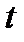

до 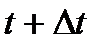называется вектор 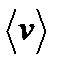, равный отношению приращения 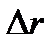радиуса-вектора точки за этот промежуток времени к его продолжительности :

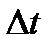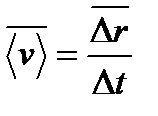
Средняя скорость направлена так же, как вектор перемещения 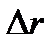, то есть вдоль хорды, стягивающей соответствующий участок траектории точки.

Скоростью точки в момент времени 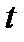называется вектор 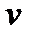, равный первой производной по времени от радиуса-вектора этой точки:

.

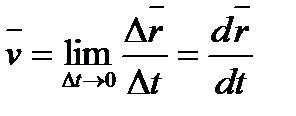
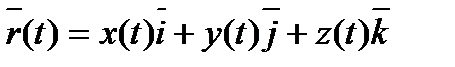Вектор 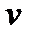можно разложить по базису 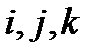, то есть на три составляющие по осям прямоугольной декартовой системы координат.

.

.

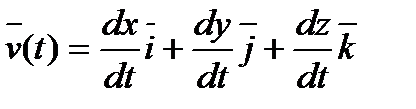
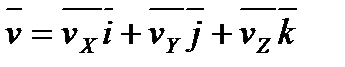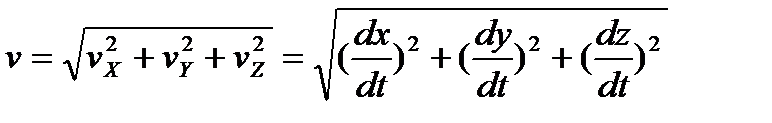Вектором средней скорости (v) называется отношение приращения (дельта)градиуса-вектора точки к промежуткувремени At:

Направление вектора средней скорости совпадает с направлением (дельта)г. При неограниченном уменьшении At средняя скорость стремится к предельному значению, которое называется мгновенной скоростью v:

Ускорение – это величина, показывающая, как изменяется скорость за одну секунду.

Ускорение.

Ускорение- векторная физическая величина, характеризующая быстроту изменения скорости .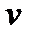

Ускорением называется вектор 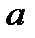, равный первой производной по времени 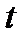от скорости 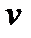этой точки. Ускорение точки также равно второй производной по времени от радиуса-вектора 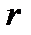этой точки:

.

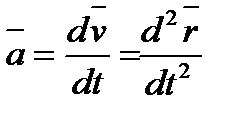Разложение ускорения точки по базису 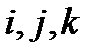, то есть на составляющие по осям прямоугольной декартовой системы координат, имеет вид:

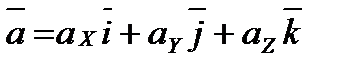, где

, , .

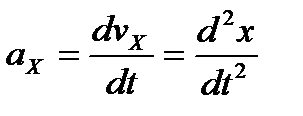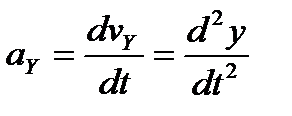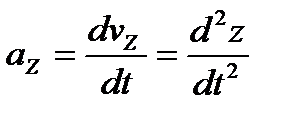Здесь 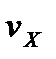, , 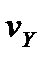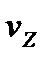- компоненты скорости точки, а 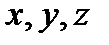- координаты точки в рассматриваемый момент времени.

За единицу скорости принимают скорость такого равномерного прямолинейного движения, при котором тело за одну секунду перемещается на один метр.

Ускорение – это величина, показывающая, как изменяется скорость за одну секунду.