Характеристики современных нейропакетов

• Нейропакет NeuroSolutions(помимо традиционных нейросетевых парадигм нейропакет включает в себя мощный редактор визуального проектирования нейронных сетей, позволяющий создавать любые нейронные структуры и алгоритмы их обучения, а также вводить собственные критерии обучения.)

• Нейропакет NeuralWorks Professional II/Plus(позволяет создавать собственные нейронные структуры.)

• Нейропакет Process Advisor(для решения задач управления динамическими процессами)

• Нейропакет NeuroShell 2(для моделирования многослойных сетей, сетей Кохонена и т. д.)

• Нейропакет BrainMaker Pro(использует алгоритм обратного распространения ошибки и имеет много настроек алгоритма обучения)

17. Экспертная система (ЭС) и ее отличие от других систем ИИ. Архитектура ЭС.

Под экспертной системой понимается программная система, которая моделирует рассуждения человека - эксперта в некоторой определенной предметной области, используя базу знаний, содержащую факты и правила об этой области и некоторый механизм логического вывода результата экспертизы.

Достоинство экспертных систем заключается в возможности принятия решений в уникальных ситуациях, для которых алгоритм заранее не известен и формируется по исходным данным в виде цепочки рассуждений (правил принятия решений) из базы знаний.

Экспертные системы отличаются и от других видов программ из области искусственного интеллекта по следующим признакам:

o ЭС в процессе решения строят алгоритм, заранее он не известен.

o Экспертные системы имеют дело с предметами реального мира, операции с которыми обычно требуют наличия значительного опыта, накопленного человеком.

o Экспертная система должна обладать способностью объяснить, почему предложено именно такое решение, и доказать его обоснованность.

Архитектура ЭС.

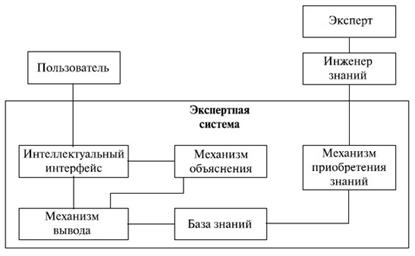База знаний - это совокупность единиц знаний.

В качестве методов представления знаний используются правила:

Если < условие >

То <заключение> CF (фактор определенности) <значение>

Интеллектуальный интерфейс воспринимает сообщения пользователя и преобразует их в форму представления базы знаний и, наоборот, переводит внутреннее представление результата обработки в формат пользователя и выдает сообщение на требуемый носитель.

Механизм вывода. Этот программный инструментарий получает от интеллектуального интерфейса запрос, формирует из базы знаний конкретный алгоритм решения задачи, выполняет алгоритм, а полученный результат предоставляется интеллектуальному интерфейсу для выдачи ответа на запрос пользователя.

Механизм объяснения.

Система всегда может выдать цепочку рассуждений до требуемой контрольной точки, сопровождая выдачу объяснения заранее подготовленными комментариями.

Механизм приобретения знаний.

В простейшем случае используется интеллектуальный редактор, который позволяет вводить единицы знаний в базу и проводить их синтаксический и семантический контроль, например, на непротиворечивость.

18. Нечеткое множество. Отличие нечеткой логики от теории вероятности. Операции над нечеткими множествами.

Нечёткое (или размытое, пушистое) множество — чёткое множество+ характеристическая функция, принимающая любые значения в интервале .

Множество – совокупность независимых, различных, неупорядоченных элементов.

Критерий оценки	Нечеткая логика	Вероятностная логика
Значения истинности	Интервал [0,1] Истинное значение – субъективная величина.	Меры истинности: существование различных исходов событий с какой-то степенью вероятности. Вероятность определяется в статистическом смысле.
Основные логические формулы	Логические формулы такие же, как и в четкой, но принимают значения истины н­­а интервале [0,1].	Всем логическим формулам приписывается вероятность, с которой эта формула будет работать так, а не иначе. Логическая формула может вести себя по-разному с какой-то вероятностью.
Правила вывода	Верны всегда. Но интерпретация полученного результата субъективна.	Правила вывода верны с какой-то степенью вероятности, которая является статистической величиной. Результат зависит от того, как сработает правило в конкретной ситуации.
Расширяемость	Все знания прописаны жестко. Возможность добавления новых знаний отсутствует.	Все знания прописаны жестко. Возможность добавления новых знаний отсутствует.

Операции над нечёткими множествами:

· операции пересечения и объединения нечётких множеств, определяемые, соответственно, операциями минимум и максимум над значениями принадлежности.

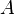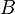· Произведением нечётких множеств и называется нечёткое подмножество с функцией принадлежности:

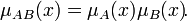
· Суммой нечётких множеств 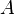и 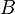называется нечёткое подмножество с функцией принадлежности:

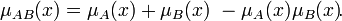
· Отрицанием множества 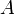называется множество 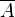с функцией принадлежности:

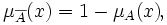
19. История и современное состояние систем нечеткой логики. Архитектура систем управления с нечеткой логикой.

История нечеткой логики

Впервые термин нечеткая логика был введен американским профессором азербайджанского происхождения Лотфи Заде в 1965 году.

В начале 1920-х годов польский математик Лукашевич трудился над принципами многозначной математической логики, в которой значениями предикатов могли быть не только «истина» или «ложь».
В 1937 г. еще один американский ученый Макс Блэк в своей статье в журнале «Философия науки» впервые применил многозначную логику Лукашевича к спискам как множествам объектов и назвал такие множества неопределенными. И только почти через 30 лет после этой работы Блэка Заде на основе логики Лукашевича построил полноценную алгебраическую систему. Мамдани в 1975 г. спроектировал первый функционирующий на основе алгебры Заде контроллер, управляющий паровой турбиной.

Фундаментальные математические операции нечеткой логики настолько четко определены, что они давно и успешно реализованы «в железе» (точнее, в системах команд) серийно выпускаемых микроконтроллеров.
В Японии это направление переживает настоящий бум. Здесь функционирует специально созданная организация – Laboratory forInternational Fuzzy Engineering Research (LIFE). Программой этой организации является создание более близких человеку вычислительных устройств.