Разработка алгоритма умножения
Разработка алгоритма умножения
Перевод сомножителей из десятичной системы счисления в четверичную:
Множимое:
_36| 4
36|9| 4
08|2
| * | 0,25 4 |
| * | 1,00 |
| 4 | |
| * | 0,00 |
| 4 | |
| 0,00 |
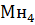 =210,100
=210,100
 =100111,001111
=100111,001111
Множитель:
_47| 4
4 |11| 4
| * | 0,51 4 |
| * | 2,04 |
| 4 | |
| * | 0,16 |
| 4 | |
| 0,64 |
_78|2
43
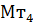 =233,200
=233,200
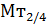 =100000,101111
=100000,101111
Запишем сомножители в форме с плавающей запятой в прямом коде:
Мн = 0,100111001111 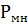 = 0.1100 (закодировано по заданию)
= 0.1100 (закодировано по заданию)
Мт = 0,100000101111  = 0.1100
= 0.1100
Умножение двух чисел с плавающей запятой на 2 разряда множителя одновременно в прямых кодах сводится к сложению порядков, формированию знака произведения, преобразованию разрядов множителя согласно алгоритму и перемножению мантисс сомножителей.
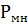 = 0.1100 = 0.1100 | +3 |
 = 0.1100 = 0.1100 | +3 |
| P = 0.0110 | +6 |
Результат закодирован в соответствии с заданием на кодировку множимого.
Знак произведения определяется суммой по модулю два знаков сомножителей:
знМн  зн Мт = 0 + 0 = 0
зн Мт = 0 + 0 = 0
Для умножения мантисс необходимо предварительно преобразовать множитель, чтобы исключить диаду 11 (34), заменив ее на триаду 101 и диаду 10 (24).
Преобразованный множитель имеет вид:
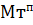 =
= 
Мн = 0,0210100
2Мн = 0,1020200
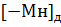 = 3,3123300
= 3,3123300
Умножение по алгоритмуВ
| 0,000000000000 | 11,111111111111111111111111 | 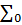 |
| 0,000000210100 | 11,111111111111100111011111 | 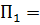 Мн Мн |
| 0,000000210100 | 11,111111111111100111011111 | 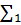 |
| 0,000002101000 | 11,111111111110011101111111 | 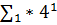 |
| 3,333333123100 | 00,000000000000011000011111 | 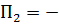 Мн Мн |
| 0,000001230300 | 11,111111111101100011001111 |  |
| 0,000012303000 | 11,111111110110001100111111 |  |
| 0,000123030000 | 11,111111011000110011111111 |  |
| 3,333333123100 | 00,000000000000011000011111 | 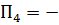 Мн Мн |
| 0,000122213300 | 11,111111011010100100001111 | 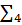 |
| 0,001222133000 | 11,111101101010010000111111 | 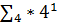 |
| 0,000001020200 | 11,111111111101111011101111 |  Мн Мн |
| 0,001223213200 | 11,111101101000100100101111 | 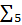 |
| 0,012232132000 | 11,110110100010010010111111 |  |
| 0,122321320000 | 11,011010001001001011111111 | 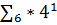 |
После окончания умножения необходимо оценить погрешность вычислений. Для этого полученное произведение  = 0,122321320000, (
= 0,122321320000, (  *
* 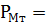 6) приводится к нулевому порядку, а затем переводится в десятичную систему счисления:
6) приводится к нулевому порядку, а затем переводится в десятичную систему счисления:
 = 122321,320000
= 122321,320000
 = 1722,2375
= 1722,2375
Результат прямого перемножения операндов дает следующее значение:
 = 1721,875
= 1721,875
Абсолютная погрешность:
Δ = 1722,2375- 1721,875 = 0,3625
δ 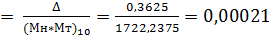 ; δ =
; δ = 
Эта погрешность получена за счет приближенного перевода из десятичной системы счисления в четверичную обоих сомножителей, а также за счет округления полученного результата произведения.
Разработка функциональных схем основных узлов
Синтез одноразрядного четверичного умножителя
ОЧУ - это комбинационное устройство, имеющее 5 входов и 3 выхода:
· 2 разряда из регистраМн, преобразованные в ФДК;
· 2 разряда из регистра Мт, преобразованные в ПМ;
· управляющий вход h.
Разряды множителя закодированы в обыкновенной двоичной с/с:
0 - 00; 1 - 01; 2 - 10; 3 - 11.
Разряды множимого закодированы в соответствии с заданием:
0 - 11; 1 - 01; 2 - 10; 3 - 00.
Управляющий вход h определяет тип операции:
0 - умножение закодированных цифр, поступивших на информационные входы ОЧУ.
1 - вывод на выходы без изменения значения разрядов, поступивших из регистра множимого.
Принцип работы ОЧУ описывается с помощью таблицы истинности.
Таблица истинности ОЧУ
| Мн | Мт | Упр. | Ст. разряд | Мл.разряд | Пример | ||||
 |  |  |  | h |  |  |  |  | |
| 3·0=00 | |||||||||
| Выход - код «03» | |||||||||
| 3·1=03 | |||||||||
| Выход - код «03» | |||||||||
| 3·2=12 | |||||||||
| Выход - код «03» | |||||||||
| x | x | x | x | 3·3=21 | |||||
| x | x | x | x | Выход - код «03» | |||||
| 1·0=00 | |||||||||
| Выход - код «01» | |||||||||
| 1·1=01 | |||||||||
| Выход - код «01» | |||||||||
| 1·2=02 | |||||||||
| Выход - код «01» | |||||||||
| x | x | x | x | 1·3=03 | |||||
| x | x | x | x | Выход - код «01» | |||||
| 2·0=00 | |||||||||
| Выход - код «02» | |||||||||
| 2·1=02 | |||||||||
| Выход - код «02» | |||||||||
| 2·2=10 | |||||||||
| Выход - код «02» | |||||||||
| x | x | x | x | 2·3=12 | |||||
| x | x | x | x | Выход - код «02» | |||||
| 0·0=00 | |||||||||
| Выход - код «00» | |||||||||
| 0·1=00 | |||||||||
| Выход - код «00» | |||||||||
| 0·2=00 | |||||||||
| Выход - код «00» | |||||||||
| x | x | x | x | 0·3=00 | |||||
| x | x | x | x | Выход - код «00» |
В таблице выделено 8 безразличных набора, т.к. на входы ОЧУ из разрядов множителя не может поступить “11”.
Проведём минимизацию переключательных функций картами Карно-Вейча. Для проведения минимизации переключательных функций необходимо выделить те наборы переменных, где функция принимает нулевое значение. Также необходимо включить и все безразличные наборы, то есть наборы, которые не могут прийти на вход схемы ОЧУ.
Из таблицы истинности видно, что функция  всегда равна «1».
всегда равна «1».
Минимизация функции  картами Карно:
картами Карно:
  | ||||||||
 | * | * |  0 0 | |||||
| * | * | |||||||
| * | * | |||||||
 | * | * |  0 0 |
Минимизировав функцию, получим:

Минимизация функции  картами Вейча:
картами Вейча:
 | |||||||||||
 |  0 0 | ||||||||||
| * | * | * | * |  * * | * | * | * |  | |||
 | |||||||||||
| h | h |
Минимизировав функцию, получим:

 |
 Минимизация функции
Минимизация функции  картами Карно:
картами Карно:
  |  |  010 010 |  | |||||
 0 0 | * | * |  0 0 | |||||
 | * |  * * | ||||||
| * | * | |||||||
| * | * |
Минимизировав функцию, получим:

Построенная схема – Схема 2.
Поиск L-экстремалей.
| z#(Z-z) | 1x1x0 | 1x0x1 | 0x1x1 | 0x0x0 | xxx0x |
| 1x1x0 | - | 1x0x1 | 0x1x1 | 0x0x0 | 0xx0x |
| xx00x | |||||
| xxx01 | |||||
| 1x0x1 | 1x1x0 | - | 0x1x1 | 0x0x0 | 0xx0x |
| 0x00x | |||||
| xx000 | |||||
| 0xx01 | |||||
| xx101 | |||||
| 0x1x1 | 1x1x0 | 1x0x1 | - | 0x0x0 | 0x00x |
| 0xx00 | |||||
| 0x00x | |||||
| xx000 | |||||
| 0x001 | |||||
| 1x101 | |||||
| 0x0x0 | 1x1x0 | 1x0x1 | 0x1x1 | - | 0x001 |
| 0x100 | |||||
| 0x001 | |||||
| 1x000 | |||||
| 0x001 | |||||
| 1x101 | |||||
| xxx0x | 1x110 | 1x011 | 0x111 | 0x010 | - |
| Остаток | 1x110 | 1x011 | 0x111 | 0x010 | 0x001 |
| 0x100 | |||||
| 0x001 | |||||
| 1x000 | |||||
| 0x001 | |||||
| 1x101 |
| z#(Z-z) n L | ||||||||
| 1x110 | Ø | Ø | Ø | Ø | Ø | Ø | ||
| 1x011 | Ø | Ø | Ø | Ø | Ø | Ø | ||
| 0x111 | Ø | Ø | Ø | Ø | Ø | Ø | ||
| 0x010 | Ø | Ø | Ø | Ø | Ø | Ø | ||
| 0x001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x100 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 1x000 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 0x001 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| 1x101 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
Откуда получим множество L-экстремалей 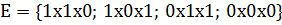
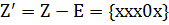
| L#E | ||||||||
| 1x1x0 | Ø | Ø | ||||||
| 1x0x1 | Ø | Ø | Ø | Ø | ||||
| 0x1x1 | Ø | Ø | Ø | Ø | Ø | Ø | ||
| 0x0x0 | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
| Остаток | Ø | Ø | Ø | Ø | Ø | Ø | Ø | Ø |
Получена единственная тупиковая форма:
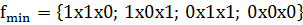
Проверка функции 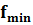 картами Карно:
картами Карно:
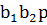 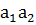 | ||||||||
 00 00 | * | * |  1 1 |  1 1 | * | * | ||
| * | * | * | * | |||||
| * |  * * |  | * |  * * | ||||
| * | * | * | * |
Минимизировав функцию, получим:
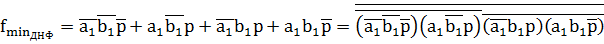
Построенная схема – Схема 3.
Литература
1. Савельев А.Я. Прикладная теория цифровых автоматов. М.: Высшая
школа, 1985.
2. Лысиков Б.Г. Арифметические и логические основы цифровыхавтома-
тов. Мн.: Вышейшая школа, 1980.
3. Лысиков Б.Г. Цифровая вычислительная техника. Мн.: , 2003 г.
4. Луцик Ю.А., Лукьянова И.В., Ожигина М.П. – Учебное пособие по
курсу "Арифметические и логические основы вычислительной техники". -Мн.: ротапринт МРТИ ,2001 г.
5. Луцик Ю.А., Лукьянова И.В.– Учебное пособие по курсу "Арифметические и логические основы вычислительной техники". -Мн.:ротапринт МРТИ ,2004 г.
Разработка алгоритма умножения
Перевод сомножителей из десятичной системы счисления в четверичную:
Множимое:
_36| 4
36|9| 4
08|2
| * | 0,25 4 |
| * | 1,00 |
| 4 | |
| * | 0,00 |
| 4 | |
| 0,00 |
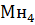 =210,100
=210,100
 =100111,001111
=100111,001111
Множитель:
_47| 4
4 |11| 4
| * | 0,51 4 |
| * | 2,04 |
| 4 | |
| * | 0,16 |
| 4 | |
| 0,64 |
_78|2
43
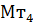 =233,200
=233,200
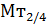 =100000,101111
=100000,101111
Запишем сомножители в форме с плавающей запятой в прямом коде:
Мн = 0,100111001111 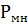 = 0.1100 (закодировано по заданию)
= 0.1100 (закодировано по заданию)
Мт = 0,100000101111  = 0.1100
= 0.1100
Умножение двух чисел с плавающей запятой на 2 разряда множителя одновременно в прямых кодах сводится к сложению порядков, формированию знака произведения, преобразованию разрядов множителя согласно алгоритму и перемножению мантисс сомножителей.
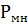 = 0.1100 = 0.1100 | +3 |
 = 0.1100 = 0.1100 | +3 |
| P = 0.0110 | +6 |
Результат закодирован в соответствии с заданием на кодировку множимого.
Знак произведения определяется суммой по модулю два знаков сомножителей:
знМн  зн Мт = 0 + 0 = 0
зн Мт = 0 + 0 = 0
Для умножения мантисс необходимо предварительно преобразовать множитель, чтобы исключить диаду 11 (34), заменив ее на триаду 101 и диаду 10 (24).
Преобразованный множитель имеет вид:
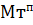 =
= 
Мн = 0,0210100
2Мн = 0,1020200
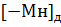 = 3,3123300
= 3,3123300
Умножение по алгоритмуВ
| 0,000000000000 | 11,111111111111111111111111 | 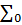 |
| 0,000000210100 | 11,111111111111100111011111 | 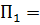 Мн Мн |
| 0,000000210100 | 11,111111111111100111011111 | 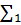 |
| 0,000002101000 | 11,111111111110011101111111 | 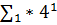 |
| 3,333333123100 | 00,000000000000011000011111 | 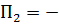 Мн Мн |
| 0,000001230300 | 11,111111111101100011001111 |  |
| 0,000012303000 | 11,111111110110001100111111 |  |
| 0,000123030000 | 11,111111011000110011111111 |  |
| 3,333333123100 | 00,000000000000011000011111 | 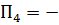 Мн Мн |
| 0,000122213300 | 11,111111011010100100001111 | 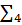 |
| 0,001222133000 | 11,111101101010010000111111 | 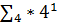 |
| 0,000001020200 | 11,111111111101111011101111 |  Мн Мн |
| 0,001223213200 | 11,111101101000100100101111 | 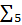 |
| 0,012232132000 | 11,110110100010010010111111 |  |
| 0,122321320000 | 11,011010001001001011111111 | 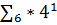 |
После окончания умножения необходимо оценить погрешность вычислений. Для этого полученное произведение  = 0,122321320000, (
= 0,122321320000, (  *
* 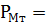 6) приводится к нулевому порядку, а затем переводится в десятичную систему счисления:
6) приводится к нулевому порядку, а затем переводится в десятичную систему счисления:
 = 122321,320000
= 122321,320000
 = 1722,2375
= 1722,2375
Результат прямого перемножения операндов дает следующее значение:
 = 1721,875
= 1721,875
Абсолютная погрешность:
Δ = 1722,2375- 1721,875 = 0,3625
δ 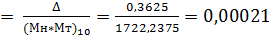 ; δ =
; δ = 
Эта погрешность получена за счет приближенного перевода из десятичной системы счисления в четверичную обоих сомножителей, а также за счет округления полученного результата произведения.
