Коэффициент корреляции. Коэффициент детерминации

Коэффициент парной корреляции используется в качес­тве меры, характеризующей степень линейной связи двух переменных. Он представляет собой ковариацию двух набо­ров данных, деленную на произведение их стандартных от­клонений:

,
.

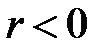Коэффициент корреляции принимает значение от -1 до +1. Если , то корреляционная связь между перемен­ными является прямой, если – обратной.

Если 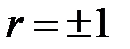, корреляционная связь представляется линейной функциональной зависимостью. При 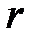=0 линейная корреляционная связь отсутствует.

Качественные характеристики связи

Значение	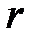Характер связи
От 0 до	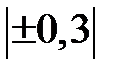Практически отсутствует
От 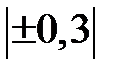до	Слабая
От до	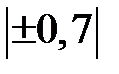Умеренная
От до	Сильная

Множественная корреляция возникает от взаимодей­ствия нескольких факторов с результативным показателем.

Значительный интерес представляют коэффициенты корре­ляции, характеризующие взаимосвязь факторов между собой. В корреляционную модель следует подби­рать независимые между собой факторы. Если коэффициент корреляции двух факторов выше 0,8, то один из этих факторов необходимо исключить из модели.

Матрица коэффициентов парной корреляции (корреляционная матрица) имеет вид

.

По данным этой матрицы можно примерно оценить, какие факторы существенно влияют на переменную 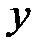, а какие – несущественно, а также выявить взаимосвязь между факторами.

Коэффициент множественной корреляции определяется по формуле

,

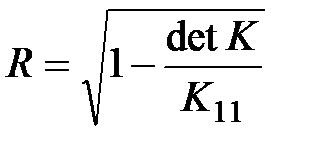где – определитель корреляционной матрицы; 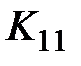– алгебраическое дополнение элемента первой строки и первого столбца матрицы 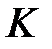. Коэффициент множественной корреляции при­нимает значения от 0 до 1. Чем ближе его значение к 1, тем в большей степе­ни учтены факторы, влияющие на зависимую переменную, тем более точной является построенная на основе отобран­ных факторов модель.

Индекс корреляции (коэффициент множественной корреляции) вычисляется по формуле

.

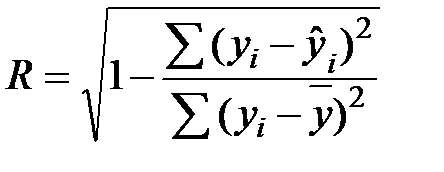Чем выше значение R, тем вероятнее близость расчетных значений результативного признака к фактическим. Данный показатель используется при любой форме связи переменных.

Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака характеризует коэффициент детерминации 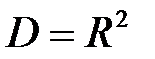, получаемый возведением в квадрат коэффициента корреляции.

О полноте связи можно судить по величине множе­ственных коэффициентов корреляции и детерминации. Например, если R = 0,92, a D = 0,85, то это значит, что вариация результативного признака на 85% зависит от изме­нения исследуемых факторов, а на долю других факторов при­ходится 15% вариации результативного показателя. Значит, в корреляционную модель удалось включить наиболее существенные факторы.

Для проверки гипотезы о статистической значимости коэффициента корреляции, т.е. гипотезы

: ,

: ,

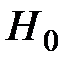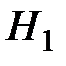при заданном уровне значимости a и объеме выборки n используется t-статистика:

.

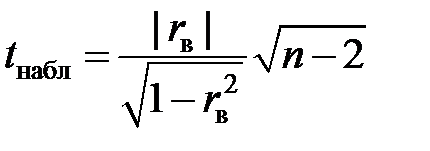По таблице критических точек распределения Стьюдента по заданному уровню значимости a и числу степеней свободы ν= n – 2 находят t_кр = t_a;n–2 для двусторонней критической области. Если t_набл£ t_кр – нет оснований отвергнуть гипотезу H₀. Если t_набл> t_кр, то гипотезу H₀ о равенстве коэффициента корреляции нулю отвергают. Другими словами, 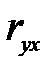значимо отличается от нуля, т. е. СВ X и Y коррелированны.

Значимость построенной модели проверяется следующим образом. Выдвигаем гипотезу : модель незначима. Конкурирующая гипотеза 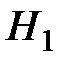: модель значима. Гипотеза проверяется по критерию Фишера. Фактическая величина

сопоставляется с таблич­ной и делается заключение о надежности связи. Здесь k – количество независимых переменных в уравнении связи. В данном случае k = 1, так как речь идет о парной регрессии. Если 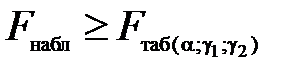со степенями свободы , 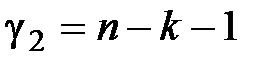при заданном уровне значимости 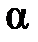, тогда линейную модель можно считать адекватной, гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность (нулевая гипотеза отвергается).

Определение меры точности модели производится с помощью расчета средней относительной ошибки аппроксимации

.

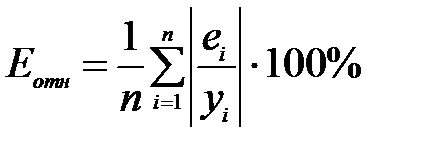Допустимый предел значений 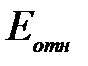составляет не более 8-15%.

Графическое представление поведения остаточного члена е:

, .

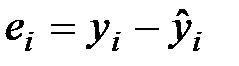позволяет проанализировать наличие авто­корреляции и гетероскедастичности (непостоянства дисперсий отклонений), с помощью графического представления от­клонений может быть обнаружена неправильная спе­цификация уравнения.

Пример 3. По данным примеров 1 и 2 вычислить коэффициент эластичности, проверить адекватность полученной модели по критерию Фишера. Сделать выводы.

Решение. Коэффициент эластичности: (или ) показывает, на сколько процентов в среднем изменяются инвестиции с изменением объема производства на 1%.

Для проверки адекватности модели используется F-статистика (критерий Фишера)

.

При заданном уровне значимости расчетное значение критерия с 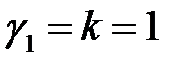, 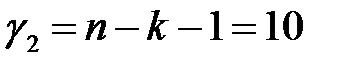степе­нями свободы больше табличного, равного 3,285, поэтому модель можно считать значимой, гипотеза о случайной природе оцениваемых характеристик отклоняется, призна­ется их статистическая значимость.