Свободное и не свободное тело.

АКСИОМЫ СТАТИКИ

Статика – это раздел теоретической механики, в котором рассматривают операции преобразования систем сил в системы, им эквивалентные, и изучают условия равновесия материальных тел под действием сил.

Аксиомы статики – это законы, установленные непосредственными наблюдениями и опытной проверкой следствий, логически вытекающих из аксиом.

Аксиома 1.Система двух сил, действующих на свободное твердое тело, является уравновешенной тогда и только тогда, когда эти силы равны по модулю и действуют вдоль одной прямой в противоположные стороны.

Аксиома 2. Если к данной системе сил добавить или отнять от нее уравновешенную систему сил, то полученная система сил будет эквивалентна исходной. Из этой аксиомы вытекает следствие: «Действие силы на твердое тело не изменится, если перенести точку приложения силы вдоль линии ее действия».

Аксиома 3(аксиома параллелограмма сил). Система двух сил, приложенных к телу в одной точке, имеет равнодействующую, приложенную в той же точке и равную геометрической сумме сил. .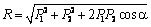

Аксиома 4(3-й закон Ньютона). Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны.

Аксиома 5(принцип отвердевания). Равновесие изменяемого (деформируемого) тела не нарушится, если тело станет абсолютно твердым. Другими словами, при равновесии деформируемого тела силы, действующие на него, удовлетворяют тем же условиям, что и для абсолютно твердого тела, но эти условия для деформируемого тела будут только необходимыми, не являясь достаточными.

Свободное и не свободное тело.

Свободнымназывают тело, которое не испытывает никаких препятствий для перемещения в пространстве в любом направлении. Если же тело связано с другими телами, которые ограничивают ею движение в одном или нескольких направ­лениях, то оно является несвободным.

3. Геометрический способ определения равнодействующей.

4. Аналитический способ определения равнодействующей.

Вычисление и построение равнодействующей сходящихся сил осуществляется по правилам векторной алгебры. Это можно сделать геометрическим и аналитическим способами.

При геометрическом способе строится векторный ( силовой ) многоугольник, замыкающая сторона которого и определяет вектор равнодействующей. Перенеся этот вектор параллельно себе в точку О пересечения линий действия сил, получаем искомую равнодействующую.

При аналитическом способе равнодействующая определяется через ее проекции на оси декартовой системы координат, которую удобно выбрать с началом в точке приложения сил О.

Момент силы относительно точки.

Момент силы относительно точки О - это вектор, модуль которого равен произведению модуля силы на плечо - кратчайшее расстояние от точки О до линии действия силы. Направление вектора момента силы перпендикулярно плоскости, проходящей через точку и линию действия силы, так, что глядя по направлению вектора момента, вращение, совершаемое силой вокруг точки О, происходит по часовой стрелке.

Теорема Вариньона.

теорема Вариньона- момент равнодействующей системы сил относительно какого-либо центра равен геометрической сумме моментов составляющих систему сил относительно того же центра. Математически В. т. выражается равенствами:

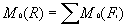В. т. пользуются при решении ряда задач механики (особенно статики), сопротивления материалов, теории сооружений и др.

Параллелепипед сил.

Простейшую пространственную систему сходящихся сил образуют три силы, приложенные к одной точке.

Для сложения таких трех сил применяется правило параллелепипеда . Если даны силы P₁, P₂ и P₃, то заменяющая их действие равнодействующая R по модулю и направлению соответствует диагонали АЕ параллелепипеда, ребра которого AB, АС и AD соответствуют трем силам. В частном случае, который наиболее характерен для решения практических задач, три данные силы P₁, P₂ и P₃ взаимно перпендикулярны и тогда при их сложении образуется прямоугольный параллелепипед.

В этом случае модуль равнодействующей
R = sqrt(P₁² + P₂² + P₃²)
а направление R относительно каждой из составляющих сил можно найти по формулам
cos α₁ = P₁/R; cos α₂ = P₂/R; cos α₃ = P₃/R. Правило параллелепипеда можно использовать не только при сложении сил, но и при разложении данной силы на три составляющие. Наиболее часто производят разложение силы на составляющие, действующие по трем взаимно перпендикулярным направлениям.

Скорость точки.

Скорость точки — это пространственно-временная мера движе­ния точки (быстроты изменения ее положения). Скорость равна первой производной по времени от расстояния в рассматриваемой системе отсчета:

Скорость точки определяется по изменению ее координат во времени. Скорость — величина векторная, она характеризует быст­роту движения и его направление. Так как скорость движений человека чаще всего не постоянная, а переменная (движение неравномерное и криволинейное), для разбора упражнений определяют мгновенные скорости.

Ускорение точки.

Ускорение точки — это пространственно-временная мера измене­ния движения точки (быстрота изменения движения — по величине и направлению скорости). Ускорение точки равно первой производной по времени от скорости этой точки в рассматриваемой системе отсчета:

Ускорение точки определяется по изменению ее скорости во времени. Ускорение — величина векторная, характеризующая быс­троту изменения скорости по ее величине и направлению в данный момент (мгновенное ускорение) .

Угловая скорость.

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

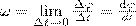
Вектор ω направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор dφ . Размерность угловой скорости dim ω = Т^-1, а ее единица — радиан в секунду (рад/с).

Линейная скорость точки

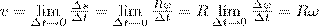
т.е

v=ωR

В векторном виде формулу для линейной скорости можно написать как векторное произведение:

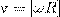
При этом модуль векторного произведения, по определению, равен ωRsin(ω, R), а направление совпадает с направлением поступательного движения правого винта его вращения от ω к R.

Если ω=const, то вращение равномерное и его можно характеризовать периодом вращения Т - временем, за которое точка совершает один полный оборот, т. е. поворачивается на угол 2π. Так как промежутку времени Δt=Т соответствует Δφ=2π, то ω=2π/T, откуда

Т = 2π/ω.

Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:

n= 1/T = ω/(2π),

откуда

ω = 2πn.

Угловое ускорение.

Угловым ускорением называется векторная величина, равная первой производной yгловой скорости по времени:

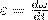
При вращении тела вокруг неподвижной оси вектор углового ускорения ε направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор ε сонаправлен вектору ω , при замедленном - противонаправлен ему.

Тангенциальная составляющая ускорения a_τ=dv/dt , v = ωR и

Нормальная составляющая ускорения

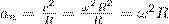
Значит, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение а_τ, нормальное ускорение а_n) и угловыми величинами (угол поворота φ, угловая скорость ω, угловое ускорение ε) выражается следующими формулами:

s = Rφ, v = Rω, а_τ = R?, a_n = ω²R.

В случае равнопеременного движения точки по окружности (ω=const)

ω = ω₀ ± ?t, φ = ω₀t ± ?t²/2,

где ω₀ — начальная угловая скорость.

Teopeмa сложения скоростей.

Пусть некоторая точка М со­вершает движение по отношению к системе отсчета Oxyz, которая са­ма движется произвольным образом по отношению к неподвижной систе­ме отсчета .

Конечно, абсолютное движение точки М определяется уравнениями

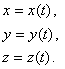
Мгновенный центр скоростей.

Мгновенным центром скоростей называется точка плоской фигуры, скорость которой в данный момент времени равна нулю.

Теорема. В каждый момент времени при плоском движении фигуры в ее плоскости при (непоступательное движение), имеется один единственный центр скоростей.

Для доказательства достаточно указать способ нахождения мгновенного центра скоростей, если известны скорость какой-либо точки О плоской фигуры и ее угловая скорость в рассматриваемый момент времени.

, , , следовательно

.Мгновенный центр скоростей находится на перпендикуляре к скорости , проведенном из точки О, на расстоянии .

Мгновенный центр скоростей это единственная точка плоской фигуры для данного момента времени. В другой момент времени мгновенным центром скоростей будет уже другая точка.

Возьмем точку Р за полюс

Так как , то . Аналогичный результат получается для любой другой точки плоской фигуры.

Скорости точек плоской фигуры определяются в данный момент так, как если бы движение фигуры было вращением вокруг мгновенного центра скоростей.

Скорости точек плоской фигуры пропорциональны их расстояниям до мгновенного центра скоростей.

Аксиомы динамики.

Первая аксиома - закон инерции.

Если на свободную материальную точку не действуют никакие силы или действует уравновешенная система сил, то точка будет находиться в состоянии покоя или равномерного прямолинейного движения.

Вторая аксиома- закон пропорциональности ускорения.

Ускорение, сообщаемое материальной точке действующей на неё силой, пропорционально этой силе и по направлению совпадает с направлением силы.

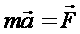Выражение называют основным законом динамики.

Третья аксиома - закон противодействия.

Силы, с которыми действуют друг на друга две материальные точки, равны по модулю и направлены вдоль прямой, соединяющей эти точки, в противоположные стороны

Четвертая аксиома - закон независимости действия сил.

При действии на материальную точку системы сил полное ускорение этой точки равно геометрической сумме ускорений от действия каждой силы

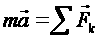
Метод кинетостатики.

Важнейшим из принципов механики является принцип Даламбера. С принципом Даламбера тесно связан метод кинетостатики — способ решения задач динамики, в котором динамические уравнения записываются в форме уравнений равновесия. Метод кинетостатики широко применяется в таких общеинженерных дисциплинах, как сопротивление материалов, теория механизмов и машин, в других областях прикладной механики. Принцип Даламбера результативно используется и внутри самой теоретической механики, где с его помощью созданы эффективные способы решения задач динамики.

Работа постоянной силы.

Работа постоянной силы. Работой постоянной силы называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла 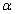между векторами силы и перемещения :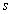

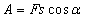
Выражение показывает, что работа является скалярной величиной и может иметь положительное или отрицательное значение в зависимости от знака косинуса угла 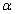Работа, совершаемая силой , положительна, если угол 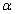между вектором силы и вектором перемещения меньше 90°.При значениях угла 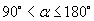работа силы отрицательна.
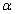Если вектор силы перпендикулярен вектору перемещения , то косинус угла равен нулю и работа силы равна нулю (рис. 65).
Единица работы в СИ называется джоулем (Дж).
Джоуль равен работе, совершаемой силой 1 Н при перемещении точки ее приложения на 1 м в направлении действия силы:

.

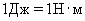Мощность.

Мощность. Мощность N — физическая величина, равная отношению работы A к промежутку времени t, в течение которого она совершена:

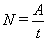
Единица мощности в СИ называется ваттом (Вт).
Ватт равен мощности, при которой совершается работа 1 Дж за время 1 с:

.

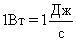В технике пользуются более крупными единицами — киловаттом и мегаваттом:

1 кВт = 10³ Вт,

1 МВт = 10⁶ Вт.

Работа, совершаемая за 1 ч при мощности в 1 кВт, называется киловатт-часом:

.

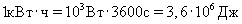Трение качения.

Если рассматриваемое тело имеет форму цилиндрического катка и под действием активных сил может катиться по поверхности другого тела, то из-за деформации поверхностей этих тел в месте их соприкосновения возникают силы реакции, препятствующие как скольжению, так и качению катка. Примерами таких катков являются различные колеса, например, колеса локомотивов, электровозов, вагонов, автомашин и т.д.

Установлены следующие приближенные законы трения качения.

Первый закон. Максимальный момент пары сил, препятствующий качению, в широких пределах не зависит от радиуса катка.

Второй закон. Максимальный момент сопротивления качению про­порционален силе нормального давления катка на опорную плоскость и дос­тигается в момент выхода катка из положения равновесия

;

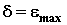
(условие начала качения катка).

Коэффициент 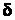называют коэффициентом трения качения или коэффициентом трения 2-го рода. Он имеет размерность длины.

Третий закон. Коэффициент трения качения зависит от материала катка, опорной плоскости, а также от физического состояния их поверхностей.

; ; .

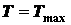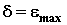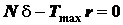Коэффициенты трения качения устанавливаются экспериментально.

Приведем значения коэффициентов трения качения для некоторых материалов (в см):

Стальной каток по стали. . . . . . . . . . . . . . . 0,005

Деревянный каток по стали . . . . . . . . . . . . . 0,03 – 0,04

Деревянный каток по дереву . . . . . . . . . . . . . 0,05 – 0,08

Колесо вагона по рельсу . . . . . . . . . . . . . . » 0,05

Резиновая шина по шоссе . . . . . . . . . . . . . .» 0,024

Коэффициент трения качения при качении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости.

Законы трения качения, как и законы трения скольжения, справедливы для не очень больших давлений и не слишком легко деформируемых материалов катка и плоскости.

Вычислим тяговую силу, необходимую для начала скольжения тела и для начала качения катка радиуса одинакового веса по горизонтальной плоскости

;

.

Обычно . Следовательно, для начала качения требуется значительно меньшая сила, чем для начала скольжения тела одинакового веса по горизонтальной плоскости. С точки зрения затрат энергии выгодно заменять скольжение качением. Изобретение колеса примерно 5000 лет назад явилось огромным достижением человечества по пути борьбы с трением.

Механический КПД.

Механический коэффициент полезного действия. Выполнение по­лезной работы машиной сопровождается преодолением вредных сопротив­лений, главным образом сил трения в подвижных частях. По этой причине полезная работа машины всегда получается меньше затраченной энергии на приведение в действие машины.

Полезная работа машины численно равна разности между затраченной энергией двигателя и работой сил сопротивлений А_n = А₃ — А_с,

где: А_n — полезная работа; А₃ — затраченная работа; А_с — работа сил со­противления.

Для оценки совершенства машины в зависимости от затраченной энер­гии и полезной работы определяют коэффициент полезного действия маши­ны (КПД).

Численная величина КПД определяется отношением полезной работы машины к потребляемой энергии:полезная работа потребляемая энергия

Вследствии наличия вредных сопротивлений коэффициент полезного действия не может быть равен единице или быть больше ее. Коэффициент полезного действия обычно выражают в процентах.

Коэффициент полезного действия можно определить также отношением полезной мощности машины к затраченной мощности двигателя:

_{_____________мощность, передаваемая механизмом потребителю}

кпд = ------------------------------------------------------------------------------------------

^{_________________мощность, подведенная к механизму}

Данное определение КПД показывает как величина мощности влияет на совершаемую механическую работу.

С целью экономии энергии конструктора все время совершенствуют ма­шины и механизмы, повышая их коэффициент полезного действия. Основ­ные пути его повышения — уменьшения трения смазкой трущихся поверх­ностей, применение подшипников трения качения, уменьшение веса по­движных частей механизмов.

Импульс силы.

ИМПУЛЬС СИЛЫ - величина, характеризующая действие, к-рое оказывает на тело сила F за нек-рый промежуток времени t₁; равна произведению ср. значения этой силы на время её действия: S=F_cp.t₁. И. с.- величина векторная и направлена так же, как F_cp. Более точно И. с. определяется интегралом

При движении материальной точки под действием силы её количество движения получает за время t₁ прирашение, равное И. с. Т. о., mv₁=mv₀+S, где mv₀ и mv₁ - соответственно кол-ва движения точки в начале и в конце промежутка времени t₁. Понятием И. с. широко пользуются в механике, в частности в теории удара ,где величина, равная пмпульсу ударной силы F_уд за время удара t, наз. ударным импульсом

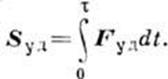
Кинетическая энергия тела.

Кинетическая энергия тела - скалярная физическая величи­на, равная половине произведения массы тела на квадрат его скорости:

.

Кинетическая энергия, как и работа, измеряется в джоулях (Дж). Кинетическая энергия зависит от скорости тела, следовательно ее значение зависит от выбора системы отсчета.

2. Теорема о кинетической энергии.

Определим физическую величину, изменяющуюся при совер­шении работы. Рассмотрим для этого движение тела массой т, скорость которого увеличивается от скорости 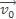до 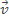и под действием всех приложенных к нему сил. Работа равнодействующей постоянной силы совпадающей по направлению с перемещением 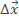, равна А = F
∆
x
. Так как F
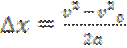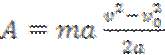= та, , то . Или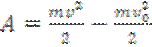

Эту формулу называют теоремой о кинетической энергии, где – кинетическая энергия в начальный момент времени.

Изменение кинетической энергии тела равно работе всех
сил, действующих на тело: Е_к-Е_к0 =А. Теорема о кинетической энергии сводится к равенству

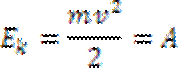
Гипотезы и допущения

Расчет реальных конструкций и их элементов является либо теоретически невозможным, либо практически неприемлемым по своей сложности. Поэтому в сопротивлении материалов применяется модель идеализированного деформируемого тела, включающая следующие допущения и упрощения:

1. Гипотеза сплошности и однородности: материал представляет собой однородную сплошную среду; свойства материала во всех точках тела одинаковы и не зависят от размеров тела.

2. Гипотеза об изотропности

материала: физико-механические свойства материала одинаковы по всем направлениям.

3. Гипотеза об идеальной упругости материала: тело способно восстанавливать свою первоначальную форму и размеры после устранения причин, вызвавших его деформацию.

4. Гипотеза (допущение) о малости деформаций: деформации в точках тела считаются настолько малыми, что не оказывают существенного влияния на взаимное расположение нагрузок, приложенных к телу.

5. Допущение о справедливости закона Гука: перемещения точек конструкции в упругой стадии работы материала прямо пропорциональны силам, вызывающим эти перемещения.

6. Принцип независимости действия сил (принцип суперпозиции): результат воздействия нескольких внешних факторов равен сумме результатов воздействия каждого из них, прикладываемого в отдельности, и не зависит от последовательности их приложения.

7. Гипотеза Бернулли о плоских сечениях: поперечные сечения, плоские и нормальные к оси стержня до приложения к нему нагрузки, остаются плоскими и нормальными к его оси после деформации.

8. Принцип Сен-Венана: в сечениях, достаточно удалённых от мест приложения нагрузки, деформация тела не зависит от конкретного способа нагружения и определяется только статическим эквивалентом нагрузки.

Эти положения ограниченно применимы к решению конкретных задач. Например, для решения задач устойчивости утверждения 4-6 не справедливы, утверждение 3 справедливо не всегда.

32. Метод сечений

Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки. Метод сечений состоит из четырех последовательных этапов: разрезать, отбросить, заменить, уравновесить.

33. Напряжение полное,нормальное,касательное

Метод сечений позволяет выявить внутренние силовые факторы. Но для оценки прочности необходимо уметь определять внутренние силы в любой точке сечения рассматриваемого бруса. Поэтому введем числовую меру интенсивности внутренних сил - напряжение.

Рассмотрим брус, к которому приложена некоторая нагрузка. Брус под действием нагрузки находится в равновесии. Применяя метод сечений, рассечем брус поперечной плоскостью, отбросим левую часть бруса, заменим действие отброшенной части на рассматриваемую системой внутренних сил. Выделим вокруг произвольной точки малую площадку 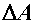(рис. а). Равнодействующую внутренних сил в пределах этой площадки обозначим .

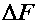Отношение 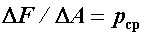называется средним напряжением. Вектор среднего напряжения совпадает по направлению с вектором равнодействующей .

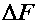При постепенном уменьшении площадки 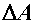изменяются как модуль, так и направление равнодействующей внутренних сил 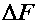, а следовательно, вектор 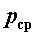постепенно приближается к истинному значению напряжения 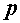в заданной точке (рис. б). Числовое значение этого напряжения выражается равенством .

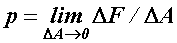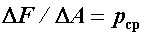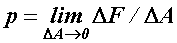Согласно формулам и , единицей напряжения служит единица силы, деленная на единицу площади. В Международной системе единиц (СИ) единица силы - Н, единица площади - 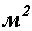, значит единица напряжения в этой системе - 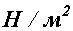названная паскалем, т.е. 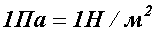. Паскаль - очень мелкая единица напряжения, поэтому более употребительной единицей является мегапаскаль: .

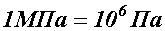Вектор 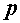полного напряжения в точке сечения можно разложить на два составляющих вектора: 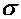и 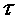(рис. а). Вектор 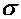, направленный перпендикулярно сечению, называется нормальным напряжением. Вектор 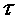, лежащий в плоскости сечения, называется касательным напряжением. Поскольку векторы 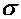и 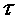взаимно перпендикулярны, зависимость между числовыми значениями напряжени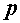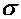й , и 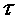выражается формулой .

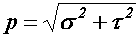Чаще оказывается целесообразным, сообразуясь с выбранными осями координат 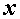, , 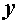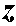(рис. б), разложить вектор 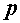не на две, а на три составляющие вектора: 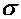(нормальное напряжение), параллельную ос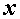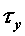и , и 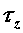(касательные напряжения), параллельные соответственно осям 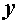и 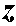. В этом случае .

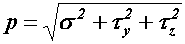Между внутренними силовыми факторами и напряжениям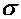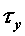и , и 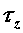существуют определенные зависимости, к установлению которых мы перейдем в следующих главах. Здесь жа заметим следующее.

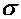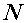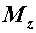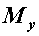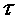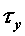Наличие нормального напряжения в любой точке поперечного сечения обусловлено возникновением в этом сечении нормальной силы или изгибающих моментов и . Наличие касательных напряжений или и 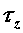обусловлено внутренними силовыми факторами, возникающими в плоскости сечения, т. е. поперечными силами 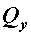, 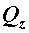или крутящим моментом .

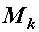34.Эпюра продольных сил

Если продольные силы, возникающие в различных поперечных сечениях стержня, неодинаковы, закон их изменения по длине стержня представляется в виде графика N(z), называемого эпюрой продольных сил. Эпюра продольных сил необходима для оценки прочности стержня и строится для того, чтобы найти опасное сечение (поперечное сечение, в котором продольная сила принимает наибольшее значение ).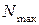

Из гипотезы плоских сечений следует: все продольные волокна стержня деформируются одинаково. Поэтому можно считать, что при растяжении (сжатии)напряжения во всех точках поперечного сечения стержня одинаковы и направлены по нормали к сечению. Такие напряжения, как уже отмечалось, называются нормальными напряжениями.

Из вышеизложенного вытекает формула нормальных напряжений при растяжении (сжатии):

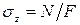
где N – продольное усилие, возникающее в данном поперечном сечении стержня, а F – площадь этого поперечного сечения.

Правило знаков для нормального напряжения ( 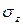), как и для продольной силы (N): при растяжении нормальное напряжение считается положительным, а при сжатии – отрицательным.

По определению относительная деформация стержня равна

,

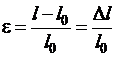где 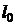, 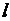– первоначальная и текущая длина стержня соответственно.

Если удлинение стержня 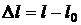вызвано действием растягивающих нормальных напряжений 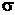, то относительная деформация

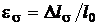
называется силовой деформацией (рис. 1.10, а). Если удлинение стержня вызвано изменением температуры 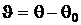, то деформация

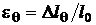
называется температурной деформацией (рис. 1.10, б).

Рис. 1.10. Силовая (а) и температурная (б) деформации

В общем случае удлинение стержня происходит за счёт действия приложенных нагрузок и изменения температуры. Поэтому

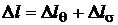
и

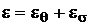. (1.16)

Как показывает опыт, силовая деформация стержня (рис. 1.10, а) пропорциональна действующим напряжениям 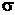, а температурная деформация стержня (рис. 1.10, б) пропорциональна приращению температуры :

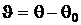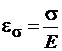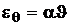, . (1.17)

Постоянная 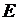называется модулем Юнга (модулем растяжения или модулем упругости первого рода), постоянная 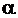– температурным коэффициентом линейного расширения. Для углеродистых сталей при комнатной температуре модуль Юнга и коэффициент линейного расширения имеют следующий порядок величины: 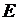» 2×1011 Па, 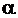» 12×10–6 К–1.

Подставляя (1.17) в (1.16), имеем

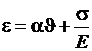(1.18)

или

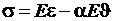. (1.19)

Равенство (1.19), как и эквивалентное ему равенство (1.18), носит название закона Гука при растяжении.

К примеру, если оба конца стержня закреплены, то его длина неизменна, а деформация 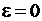. Тогда по формуле (1.16) при нагревании (охлаждении) стержня силовая деформация равна и противоположна по знаку тепловой деформации:

.

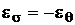Согласно (1.19) возникающие при этом напряжения равны

.

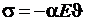Следовательно, когда приращение температуры 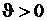, в стержне действуют сжимающие напряжения: 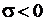. Напротив, в случае 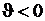в стержне возникают растягивающие напряжения: .

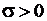Дополнение

35. ГУКА ЗАКОН - основной закон теории упругости, выражающий линейную зависимость между напряжениями и малыми деформациями в упругой среде. Установлен P. Гуком (R. Hooke) в 1660.

При растяжении стержня длиной l его удлинение 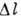пропорц. растягивающей силе F; в этом случае Г. з. имеет вид 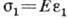, где 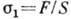- нормальное напряжение в поперечном сечении стержня, 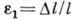- относит. удлинение, S - площадь поперечного сечения. Константа материала E наз. модулем Юнга. При этом относит. изменение поперечных размеров стержня 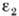пропорц. относительному удлинению: 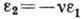. Константа 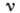наз. коэф. Пуассона

При проектировании скручиваемых круглых стержней иногда возникает необходимость учесть ограничения, накладываемые на углы закручивания различных участков стержня. В этом случае сначала строят эпюру крутящих моментов. Затем для каждого из участков стержня подбирают диаметры таким образом, чтобы выполнялось и условие прочности, и условие жесткости. При необходимости контролируют угол закручивания на всей длине стержня.

43.Полярный момент сопротивления для круга и кольца.

Полярный момент сопротивления сечения – это отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки сечения.

Для круга полярный момент сопротивления:

Wp=Jpρmax

Полярный момент сопротивления для тонкостенного кольца с достаточной точностью определяется как произведение площади кольца на его средний радиус.

44. Поперечные силы и их эпюры

Эпюры поперечных сил и изгибающих моментов нужны для наглядного представл