Аналитические формулы для моментов силы относительно координатных осей.

В основе способа лежит известное из векторной алгебры представление векторного произведения в виде определителя, что позволяет записать для вектора-момента силы следующее выражение

Здесь , - орты координатных осей; x, у, z- координаты точки приложения силы; F_x,F_y,F_z - проекции силы на координатные оси. Вспоминая, что в формуле разложения вектора на составляющие по координатному базису коэффициенты при ортах являются проекциями этого вектора на соответствующие оси, а в данном случае, по определению - моментами силы F относительно координатных осей, приходим к равенствам:

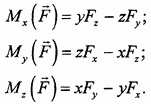
Полученные формулы называются аналитическими выражениями для моментов силы относительно координатных осей. Они позволяют вычислять моменты силы относительно координатных осей без предварительного построения момента относительно начала координат.

8)Пара сил. Момент пары как вектор. Эквивалентность пар. Свойства пар сил. Сложение пар сил. Условия равновесия системы пар сил. http://kurs.ido.tpu.ru/courses/TeorMex1_sem1/theme13.html

Дадим определение пары сил.

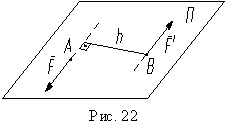
Пара сил - это система двух равных параллельных сил, направленных в разные стороны (рис. 22).

Кратчайшее расстояние между линиями действия сил называют плечом пары h , а плоскость П, где лежит пара сил, является плоскостью пары.

Пары сил реально существуют в природе. Ярким примером являются силы, действующие на стороны рамки с током в магнитном поле. На этом физическом явлении основана работа всех электродвигателей постоянного тока.

Свойства пары сил. Сформулируем, а затем докажем первое свойство.

Первое свойство. Пару сил нельзя привести к силе. Иными словами пара сил (как и сила) является самостоятельным элементом статики.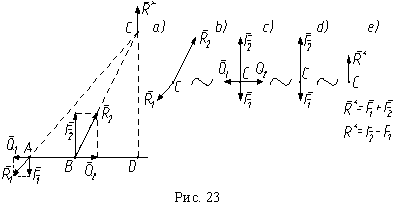

При изучении динамики мы покажем, что под действием пары сил свободное твердое тело может только поворачиваться. Следовательно, в этом параграфе мы будем изучать свойства нового самостоятельного элемента статики, под действием которого, в отличие от силы, свободное твердое тело может только поворачиваться.

Для доказательства рассмотрим сложение параллельных сил. Сложим две неравные параллельные силы, направленные в разные стороны (рис. 23). Добавляем к исходной системе сил (F₁,F₂) уравновешенную систему сил (Q₁,Q₂) ~ 0. По аксиоме параллелограмма, силы, приложенные в точках A и B, эквивалентны двум непараллельным силам R₁ и R₂ (рис. 23, a). Согласно следствию второй аксиомы, переносим эти силы в точку пересечения их линий действия C (рис. 23, b). Используя вторую и третью аксиомы, раскладываем силы R₁ и R₂ на составляющие (рис. 23, c), а затем вычитаем уравновешенную систему сил (Q₁,Q₂). В результате получаем, что исходная система сил эквивалентна тем же силам, но приложенным в одной точке C, то есть (F₁,F₂) = (F₁,F₂)_C (рис. 23, d). По аксиоме параллелограмма эта система, а следовательно, и исходная система сил, эквивалентна одной силе или равнодействующей (рис. 23, c):

(1)

Из рисунков видим, что равнодействующая и ее линия действия CD параллельны исходным силам, а точка D лежит вне отрезка AB.

При сложении двух параллельных сил, направленных в одну сторону, получается аналогичный результат, только величина равнодействующей будет равна R* = F₁ + F₂, а точка D будет лежать внутри отрезка AB.

Можно распространить этот вывод и на систему из n параллельных сил, добавляя к полученной равнодействующей по одной из оставшихся сил системы. В результате мы докажем, чтосистема параллельных сил приводится к одной силе или равнодействующей. Вопрос нахождения линии действия равнодействующей будет подробно рассмотрен в теме о центре параллельных сил.

Вернемся к доказательству первого свойства пары сил. Устремим величину первой силы ко второй. При F₁ 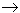F₁ из выражений (1) следует, что R* 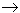0, а по рис. 22, a видим, что AC и BCстановятся параллельны друг другу. Следовательно, пара сил не может быть приведена к силе или равнодействующей, так как равнодействующая не имеет величины, а ее линия действия не определена, потому что нельзя найти точку C. Таким образом, свойство доказано.

Второе свойство. Действие пары сил на твердое тело определяется моментом пары, который является свободным вектором, перпендикулярным плоскости пары, численно равным произведению силы на плечо пары.

Ранее мы показали, что пара сил не может быть приведена к силе, а является самостоятельным элементом статики. Выясним, как пара сил действует на твердое тело. Выберем в пространстве произвольный центр O (рис. 24) и вычислим относительно этого центра сумму моментов сил, образующих пару. Эту сумму мы назовем моментом пары. Положение точек приложения сил пары относительно центра O определим радиус-векторами r₁, r₂ и, учитывая, что F' = -F, получим

(2)

Строим вектор BA, который определяет положение точки A относительно B, и на рис. 24 видим, что r₁ = r + BA или r₁ - r = BA. Учитывая это, из выражения (2) получаем

(3)

Таким образом, действие пары сил на тело определяется ее моментом, который является мерой действия пары сил на твердое тело.

Так как центр O выбран произвольно, то момент пары не зависит от выбора центра, то есть является свободным вектором. По определению векторного произведения он перпендикулярен плоскости пары (в этой плоскости лежат перемножаемые векторы BA и F) и направлен так, что с его конца вращение тела под действием пары сил наблюдается против хода часов (как и вращение BA к F по кратчайшему угловому расстоянию). Это отражено на рис. 24. Величину момента пары найдем, определяя модуль векторного произведения в (3), учитывая (рис. 24), что BA sin(BA ^ F) = h:

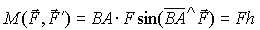(4)

Приняв за центр O последовательно точки приложения сил A и B, по формуле (2) имеем

(5)

Эта формула имеет важное значение при решении задач, когда нужно вычислять суммы моментов пар сил относительно точки.

Так как момент пары является свободным вектором, то он не имеет фиксированной точки приложения, а имеет только свой модуль и свое направление и приложить его можно в любой точке твердого тела. Это принципиальное отличие момента пары от момента силы относительно центра (точки), являющегося связанным вектором, приложенным в центре, и от скользящего вектора, примером которого является сила, приложенная к твердому телу, которую можно переносить только вдоль линии ее действия.