Модуль 4.Числовые характеристики случайных величин и векторов
Цель модуля:На основе расширения понятия интеграла как интеграла от непрерывной функции по вероятностной мере определить понятия числовых характеристик. Показать на основе механической и геометрической интерпретации распределения вероятностной меры вероятностный смысл числовых характеристик. Научиться вычислять значения числовых характеристики понимать их роль в изучении особенностейзаконов распределения случайных величин.
Использование определения интеграла Римана-Стилтьеса от непрерывной функции 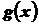 по вероятностной функции P позволяет в единой форме и независимо от типа случайной величины
по вероятностной функции P позволяет в единой форме и независимо от типа случайной величины 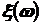 , определять:
, определять:
а) законы распределения функций случайных величин;
б) значения различных числовых характеристик случайных величин.
И в определении интеграла Римана, и в определении интеграла Римана-Стилтьеса областьQ 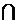 W, по которой производится интегрирование, разбивается на отрезки
W, по которой производится интегрирование, разбивается на отрезки 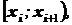
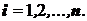 В определении интеграла Римана при составлении интегральных сумм Дарбу используется мера Лебега – длина этих отрезков:
В определении интеграла Римана при составлении интегральных сумм Дарбу используется мера Лебега – длина этих отрезков: 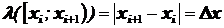 . В определении интеграла Римана-Стилтьеса при составлении интегральных сумм, аналогичных суммам Дарбу, используется вероятностная мера этих отрезков:
. В определении интеграла Римана-Стилтьеса при составлении интегральных сумм, аналогичных суммам Дарбу, используется вероятностная мера этих отрезков: 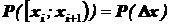 . В зависимости от типа вероятностной функции P интеграл Римана-Стилтьеса есть или сумма числового ряда, или определённый интеграл Римана.
. В зависимости от типа вероятностной функции P интеграл Римана-Стилтьеса есть или сумма числового ряда, или определённый интеграл Римана.
Закон распределения случайной величины, записанный в одной из его форм с помощью вероятностной функции P или с помощью функции распределения 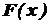 , даёт нам всю информацию об исследуемой случайной величине
, даёт нам всю информацию об исследуемой случайной величине 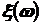 . Числовые характеристики дают меньше информации о характере распределения возможных значений случайной величины
. Числовые характеристики дают меньше информации о характере распределения возможных значений случайной величины 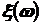 , но в них аккумулированы наиболее характерные её свойства, которые позволяют нам судить о некоторых важнейших особенностях случайной величины. Такими характеристиками являются начальные и центральные моменты случайной величины, а так же – функции от них.
, но в них аккумулированы наиболее характерные её свойства, которые позволяют нам судить о некоторых важнейших особенностях случайной величины. Такими характеристиками являются начальные и центральные моменты случайной величины, а так же – функции от них.
Наиболее употребительными числовыми характеристиками являются математическое ожидание– среднее значение случайной величины и дисперсия– мера рассеяния, разброса значений случайной величины около её математического ожидания.
Знание числовых значений математического ожидания и дисперсии служит задаче формулирования выводов о случайной величине и первичного представления о характере распределения её возможных значений.
При исследовании многомерной случайной величины, помимо математических ожиданий и дисперсий её компонент, рассматриваются ковариационные моменты, показывающие наличие и силу статистической связи между компонентами. Если статистические связи между компонентами имеют линейный характер, то в качестве оценки силы этой связи используется коэффициент линейной корреляции.
Функция регрессии, какого бы вида она ни была, описывает изменение значений условных математических ожиданий одной из компонент случайного вектора при изменении другой компоненты. То есть функция регрессии описывает изменение средних значений одной из случайных величин, когда другая случайная величина изменяется в области своих возможных значений.
Модуль 5. Классическая предельная проблема теории вероятностей
Цель модуля:Показать, что решение многих практических задач (в математике и механике, экономике и финансах, физике и химии, биологии и геологии и т.п.) базируется на основе знания законов распределения случайных величин, являющихся суммами большого числа независимых случайных величин – факторов.Знание результатов решения классической предельной проблемы позволит принимать план действий и делать обоснованные выводы при решении задач математической статистики.
В предельной проблеме теории вероятностей изучаются законы распределения случайных величин, являющиеся суммамислучайных величин: 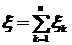 , когда число слагаемых неограниченно возрастает
, когда число слагаемых неограниченно возрастает 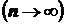 . Проблема называется классической потому, что мы рассматриваем последовательности
. Проблема называется классической потому, что мы рассматриваем последовательности 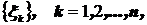 только таких случайных величин, у которых существует конечный начальный момент второго порядка, то есть
только таких случайных величин, у которых существует конечный начальный момент второго порядка, то есть 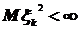 .
.
Придерживаясь исторического аспекта в изложении предельной проблемы, сначала рассматриваем случайную величину, имеющую биномиальное распределение вероятностей 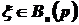 .
.
1) Если проводится большое число повторных независимых испытаний (n – велико), то решение практических задач проводится путём применения локальной и интегральной теорем Муавра-Лапласа, согласно которым:
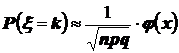 , где
, где 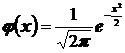 , где
, где 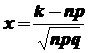 .
.
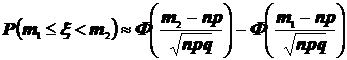 , где
, где 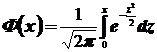 .
.
Суть этих теорем состоит в том, что при больших значениях n биномиальное распределение вероятностей хорошо аппроксимируется нормальным распределением N 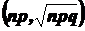 . Причём с увеличением n точность аппроксимации возрастает.
. Причём с увеличением n точность аппроксимации возрастает.
То есть из интегральной теоремы Муавра-Лапласа следует, что для функции распределения случайной величины 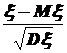 будет справедливо:
будет справедливо:
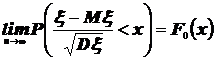 , где
, где 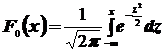 - функция распределения нормального закона N(0,1).
- функция распределения нормального закона N(0,1).
2) Случайная величина 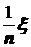 есть относительная частота наступления события Aпри проведении n испытаний. Теорема Бернулли утверждает, что при неограниченном увеличении числа испытаний с вероятностью близкой к единице, то есть практически достоверно, можно утверждать, значения относительной частоты будут очень мало отличаться от p -вероятности наступления события A в одном испытании:
есть относительная частота наступления события Aпри проведении n испытаний. Теорема Бернулли утверждает, что при неограниченном увеличении числа испытаний с вероятностью близкой к единице, то есть практически достоверно, можно утверждать, значения относительной частоты будут очень мало отличаться от p -вероятности наступления события A в одном испытании:
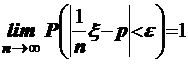 .
.
Суть этой теоремы состоит в том, что при неограниченном увеличении n относительная частота с вероятностью близкой к единице ведёт себя как постоянная величина p.
3) Если вероятность p наступления события A в одном испытании «очень мала», а проводится большое число испытаний то, согласно теореме Пуассона, хорошую аппроксимацию биномиального распределения вероятностей возможных значений случайной величины  можно получить, используя распределение Пуассона, то есть:
можно получить, используя распределение Пуассона, то есть:
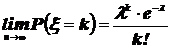 , где
, где 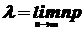 .
.
Случайная величина  ,
, 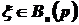 , является суммой n независимых бернуллиевских случайных величин
, является суммой n независимых бернуллиевских случайных величин 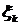 ,
, 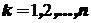 , каждая из которых есть результат проведения одного испытания,
, каждая из которых есть результат проведения одного испытания, 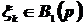 . То есть:
. То есть: 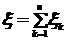 . Так как
. Так как 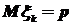 и
и 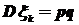 , то, заменив
, то, заменив 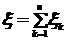 , интегральную теорему Муавра-Лапласа можно переписать так:
, интегральную теорему Муавра-Лапласа можно переписать так:
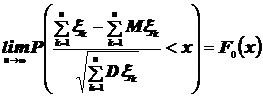 .
.
Случайную величину 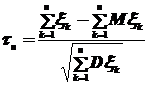 будем называть центрированной и нормированной суммой.
будем называть центрированной и нормированной суммой.
Интегральную теорему Муавра-Лапласа можно теперь сформулировать так:
Если 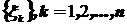 , последовательность независимых, одинаково распределённых бернуллиевских случайных величин, то, при
, последовательность независимых, одинаково распределённых бернуллиевских случайных величин, то, при  , последовательность функций распределения случайных величин
, последовательность функций распределения случайных величин 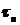 сходится к функции распределения нормального закона N(0,1):
сходится к функции распределения нормального закона N(0,1):
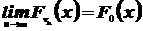 .
.
Аналогично теорему Бернулли можно, переписать так:
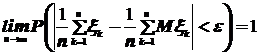 .
.
Если обозначить: 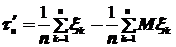 , то теорему Бернулли сформулируем так:
, то теорему Бернулли сформулируем так:
Если 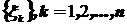 , последовательность независимых, одинаково распределённых бернуллиевских случайных величин, то, при
, последовательность независимых, одинаково распределённых бернуллиевских случайных величин, то, при 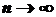 , случайная величина
, случайная величина 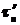 с вероятностью близкой к единице принимает значения, мало отличающиеся от нуля:
с вероятностью близкой к единице принимает значения, мало отличающиеся от нуля:
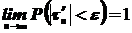 .
.
Обращаясь к теореме Пуассона, рассмотрим «двойную» последовательность бернуллиевских случайных величин 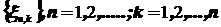 . Для каждого nслучайные величины
. Для каждого nслучайные величины 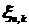 ,
, 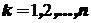 , имеют одинаковое распределение
, имеют одинаковое распределение 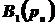 . Вероятности
. Вероятности 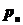 уменьшаются с изменением n. Обозначим
уменьшаются с изменением n. Обозначим 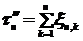 .
.
Теорема Пуассона:
Если 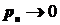 , но так что
, но так что 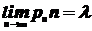 , то, при
, то, при 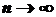 , случайная величина
, случайная величина 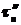 имеет распределение вероятностей мало отличающееся от распределения вероятностей закона Пуассона, то есть:
имеет распределение вероятностей мало отличающееся от распределения вероятностей закона Пуассона, то есть:
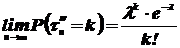 .
.
Суммируя всё, можем сказать, что для случайной величины  , являющейся суммой независимых бернуллиевских случайных величин
, являющейся суммой независимых бернуллиевских случайных величин 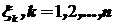 , в качестве предельного распределения вероятностей при
, в качестве предельного распределения вероятностей при 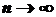 будет нормальное, вырожденное или пуассоновское распределение вероятностей.
будет нормальное, вырожденное или пуассоновское распределение вероятностей.
Естественно возникает вопрос: «А если снять ограничение, состоящее в том, что случайные величины 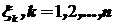 - бернуллиевские? Какие ограничения надо наложить на последовательностьслучайных величин
- бернуллиевские? Какие ограничения надо наложить на последовательностьслучайных величин 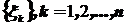 , чтобы их суммы
, чтобы их суммы 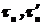 и
и 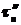 в качестве предельного при
в качестве предельного при 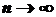 имели, соответственно, нормальное, вырожденное и пуассоновское распределение вероятностей?».
имели, соответственно, нормальное, вырожденное и пуассоновское распределение вероятностей?».
Определяем три новых понятия: «Закон больших чисел», «Центральная предельная теорема» и «Закон малых чисел». Знакомимся с теоремами, в которых на последовательностислучайных величин 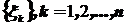 налагаются ограничения, при которых:
налагаются ограничения, при которых:
1) 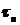 имеет распределение, мало отличающееся от нормального (
имеет распределение, мало отличающееся от нормального ( 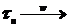 N(0,1));
N(0,1));
2) 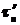 имеет распределение, мало отличающееся отвырожденного (
имеет распределение, мало отличающееся отвырожденного ( 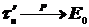 );
);
3) 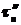 имеет распределение, мало отличающееся от распределения Пуассона (
имеет распределение, мало отличающееся от распределения Пуассона ( 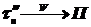 (
( 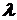 )).
)).
Необходимо уметь объяснить практическую значимость предельных теорем для последовательностей независимых случайных величин.
Математическая статистика
Модуль 6. Первичная обработка статистических данных. Точечные оценки числовых характеристик
Цель модуля:Узнать новую терминологию, понятия и определения математической статистики. Показать приёмы и правила первичной обработки статистических данных, принципы выбора точечных оценок числовых характеристик изучаемых случайных величин.
Математическая статистика - самостоятельная математическая дисциплина, имеющая свой словарь терминов, с которым мы знакомимся, как и при изучении теории вероятностей, путём введения основных понятий и определений. Изучение свойств введённых терминов и формулирование выводов, которые делаются по результатам обработки статистических данных, проводятся путём использования основных положений теории вероятностей.
Надо всё время иметь в виду, что все объекты и построения математической статистики являются экспериментальными моделями объектов и построений, которые вводились и изучались в теории вероятностей.
Первыми основными понятиями являются понятия «генеральная совокупность» и «выборка».
Генеральная совокупность– это все объекты, обладающие интересующим нас количественным признаком. Исследуемый количественный признак – случайная величина. Каждый объект генеральной совокупности имеет определённое значение количественного признака. Это значение количественного признака является одним из возможных значений случайной величины. Наблюдая объекты генеральной совокупности, мы фиксируем возможные значения случайной величины. Частота встречаемости возможных значений случайной величины определяется законом распределения вероятностей этой случайной величины.
Однако не всегда удаётся, а иногда просто невозможно, обследовать все объекты генеральной совокупности для определения значения количественного признака, которым они обладают. Для изучения случайной величины из генеральной совокупности отбирают некоторое количество объектов и определяют значения количественного признака, которым обладают эти объекты.
Полученные значения количественного признака 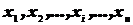 у этих объектов будут называться статистическими данными или выборкой из генеральной совокупности, если они репрезентативны. Под термином репрезентативность (представительность) мы понимаем, что полученные данные вполне отражают в общих чертах особенности количественного признака, которым обладают объекты генеральной совокупности.
у этих объектов будут называться статистическими данными или выборкой из генеральной совокупности, если они репрезентативны. Под термином репрезентативность (представительность) мы понимаем, что полученные данные вполне отражают в общих чертах особенности количественного признака, которым обладают объекты генеральной совокупности.
Различные методики отбора объектов из генеральной совокупности, стремятся обеспечить репрезентативность получаемых данных. Мы отмечаем, что попадание каждого объекта в выборку должно быть независимым от остальных объектов. Измерения значений количественного признака у выбранных объектов должны проводиться по одной методике, в одинаковых условиях и одним и тем же инструментом.
Если полученная выборка 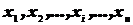 - репрезентативна, то на её элементы мы будем смотреть двояко. С одной стороны мы элементы выборки будем рассматривать как набор n чисел, являющихся значениями эмпирической случайной величины
- репрезентативна, то на её элементы мы будем смотреть двояко. С одной стороны мы элементы выборки будем рассматривать как набор n чисел, являющихся значениями эмпирической случайной величины 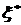 . А с другой стороны - как на n-мерный случайный вектор
. А с другой стороны - как на n-мерный случайный вектор 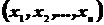 с независимыми, одинаково распределёнными компонентами.
с независимыми, одинаково распределёнными компонентами.
При первичной обработке статистических данных строится вариационный ряд, являющийся, по существу, рядом распределения эмпирической случайной величины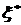 . При этом мы считаем, что все элементы выборки - равновозможные, то есть
. При этом мы считаем, что все элементы выборки - равновозможные, то есть 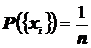 . Геометрическая иллюстрация вариационного ряда – гистограмма даёт наглядное представление о характере распределения вероятностей исследуемой случайной величины
. Геометрическая иллюстрация вариационного ряда – гистограмма даёт наглядное представление о характере распределения вероятностей исследуемой случайной величины  . Теорема Гливенко показывает, что при
. Теорема Гливенко показывает, что при 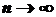 с вероятностью близкой к единице значения эмпирической функции распределения
с вероятностью близкой к единице значения эмпирической функции распределения 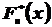 будут очень мало отличаться от значений теоретической функции распределения
будут очень мало отличаться от значений теоретической функции распределения 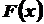 исследуемой случайной величины
исследуемой случайной величины  .
.
Случайная величина  имеет числовые характеристики
имеет числовые характеристики 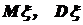 и другие. Значения этих характеристик мы не знаем, это – теоретические числа. По элементам выборки мы должны оценить эти теоретические числа - дать их точечные оценки. Так как эмпирическая случайная величина
и другие. Значения этих характеристик мы не знаем, это – теоретические числа. По элементам выборки мы должны оценить эти теоретические числа - дать их точечные оценки. Так как эмпирическая случайная величина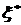 понимается нами как статистическая модель исследуемой случайной величины
понимается нами как статистическая модель исследуемой случайной величины  , то естественно принять значения числовых характеристик
, то естественно принять значения числовых характеристик 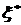 в качестве точечных оценок неизвестных значений числовых характеристик. Так как мы приняли, что
в качестве точечных оценок неизвестных значений числовых характеристик. Так как мы приняли, что 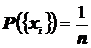 , а эмпирическая случайная величина
, а эмпирическая случайная величина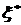 -случайная величина дискретного типа, то
-случайная величина дискретного типа, то 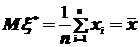 ,
, 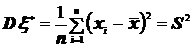 . То есть предлагается эмпирическое математическое ожидание
. То есть предлагается эмпирическое математическое ожидание 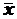 - среднее арифметическое элементов выборки и эмпирическую дисперсию
- среднее арифметическое элементов выборки и эмпирическую дисперсию 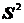 принять в качестве точечных оценок.
принять в качестве точечных оценок.
Обобщая сказанное, теоретические числовые характеристики исследуемой случайной величины обозначим  , а соответствующие эмпирические числовые характеристики, предлагаемые в качестве оценок, обозначим
, а соответствующие эмпирические числовые характеристики, предлагаемые в качестве оценок, обозначим 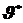 .
.
Любая точечная оценка 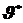 является функцией элементов выборки:
является функцией элементов выборки: 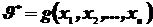 . Элементы, попавшие в выборку – случайные величины. Следовательно, функция
. Элементы, попавшие в выборку – случайные величины. Следовательно, функция 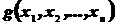 - случайная величина. Всякую функцию элементов выборки будем называть статистикой.
- случайная величина. Всякую функцию элементов выборки будем называть статистикой.
Но функций от элементов выборки можно придумать много. И каждую придуманную функцию можно предложить в качестве статистической оценки теоретической числовой характеристики. Возникает вопрос: «Как выбрать из множества предлагаемых точечных оценок наилучшую оценку?». Чтобы ответить на этот вопрос, мы должны сформулировать требования, исходящие из здравого смысла, и проверять выполнение этих требований к предлагаемым точечным оценкам. Та оценка, которая будет удовлетворять всем требованиям, будет наилучшей оценкой и будет принята в качестве точечной оценки неизвестного значения числовой характеристики.
Формулировки требований состоятельности, несмещённости и эффективности, предъявляемые к точечным оценкам, основаны на знании закона больших чисел и центральной предельной теоремы теории вероятностей. Логичность и справедливость этих требований не вызывает сомнений.
Рассматриваемые методы получения точечных оценок, позволяют обоснованным теорией вероятностей путём получать их и проверять выполнение сформулированных требований к ним.
Модуль 7. Интервальные оценки числовых характеристик
Цель модуля:Продолжить знакомство с приёмами первичной обработки статистических данных. Узнать три типа распределений случайных величин, которые используются при определении закона распределения различных функций статистических данных.
Кроме точечной оценки 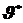 значения теоретической числовой характеристики
значения теоретической числовой характеристики  изучаемой случайной величины исследователю иногда бывает необходимо знать интервал
изучаемой случайной величины исследователю иногда бывает необходимо знать интервал 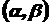 , в котором с достаточно большой степенью уверенности
, в котором с достаточно большой степенью уверенности  (0,9; 0,95; 0,999,…)может находиться неизвестное значение числовой характеристики
(0,9; 0,95; 0,999,…)может находиться неизвестное значение числовой характеристики  . То есть, при заданном уровне надёжности
. То есть, при заданном уровне надёжности ,по имеющейся выборке
,по имеющейся выборке 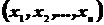 надо определить границы интервала
надо определить границы интервала 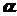 и
и 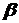 так, чтобы выполнялось неравенство:
так, чтобы выполнялось неравенство:
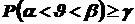 .
.
Вероятность  называетсядоверительной вероятностью, а интервал
называетсядоверительной вероятностью, а интервал 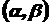 - доверительным интервалом.
- доверительным интервалом.
Ясно, что границы интервала, как функции элементов выборки, являются статистиками – случайными величинами: 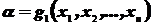 и
и 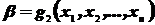 . Значит для определения при заданной доверительной вероятности их числовых значений, надо знать закон распределения вероятностей этих статистик.
. Значит для определения при заданной доверительной вероятности их числовых значений, надо знать закон распределения вероятностей этих статистик.
Наиболее часто в математической статистике используются три распределения вероятностей: распределение Пирсона, распределение Стьюдента и распределение Фишера-Снедекора. Случайные величины 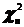 ,
, 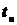 и
и 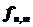 , подчиняющиеся, соответственно, этим распределениям, являются функциями независимых случайных величин, имеющих одинаковое нормальное распределение N(0,1).
, подчиняющиеся, соответственно, этим распределениям, являются функциями независимых случайных величин, имеющих одинаковое нормальное распределение N(0,1).
Применение этих трёх распределений в математической статистике основано на предположении о нормальном распределении исследуемого количественного признака, определённого на генеральной совокупности, и некоторых статистик, что, в свою очередь, обосновывается центральной предельной теоремой теории вероятностей.
