Частостями называются частоты, выраженные в долях единицы или в процентах к итогу.

Соответственно сумма частостей равна 1 или 100%.

29. В зависимости от характера вариации признака различают дискретные и интервальные вариационные ряды.

Построениеинтервальных вариационных рядов целесообразно прежде всего при непрерывной вариации признака, а также если дискретная вариация проявляется в широких пределах, т. е. число вариантов дискретного признака достаточно велико.

30. Ряд распределения - это упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку.

Вариационными называют ряды распределения, построенные по количественному признаку.

Структурная группировка разделяет однородную в качественном отношении совокупность единиц по определенным, существенным признакам на группы, характеризующие ее состав и структуру.

Что обобщает средняя величина признака?

Средняя величина признака – обобщающий показатель, характеризующий типический уровень явления.

Сущность средней заключается в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных.

Что такое ИСС (ИФС)?

Определить среднюю во многих случаях можно черезисходное соотношение средней (ИСС) или ее логическую формулу:

Правила применения средних величин:

необходимо исходить из качественного содержания признака;

средняя величина должна рассчитываться по однородной совокупности;

необходим обоснованный выбор единицы совокупности.

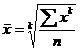Формулы расчета степенных средних можно записать в общем виде:

- простая формула,

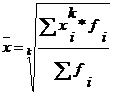- взвешенная формула.

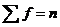
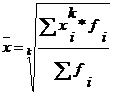Назовите виды средних величин (степенных).

Виды степенных средних:

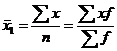при k=1 “средняя арифметическая” -

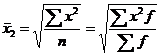при k=2 “средняя квадратическая” -

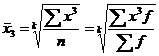при k=3 “средняя кубическая”

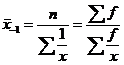при k=-1 “средняя гармоническая”

-

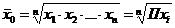“средняя геометрическая” (k=0)

Когда применяется средняя квадратическая?

Средняя квадратическая –Применяется для осреднения величин, выраженных в виде квадратных функций (например, средние диаметры колес, труб, стволов, средние стороны квадратов и др.). Используется при расчете показателей вариации (СКО).

Для чего применяется средняя геометрическая?

Средняя геометрическая обладает свойством сохранять неизменным произведение исходных величин. Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т. е. характеризует средний коэффициент роста.