Элементарные реологические тела

Простейшим реологическим телом является тело Гука (H-тело). Схематически H-тело изображено на рис. 1.2.

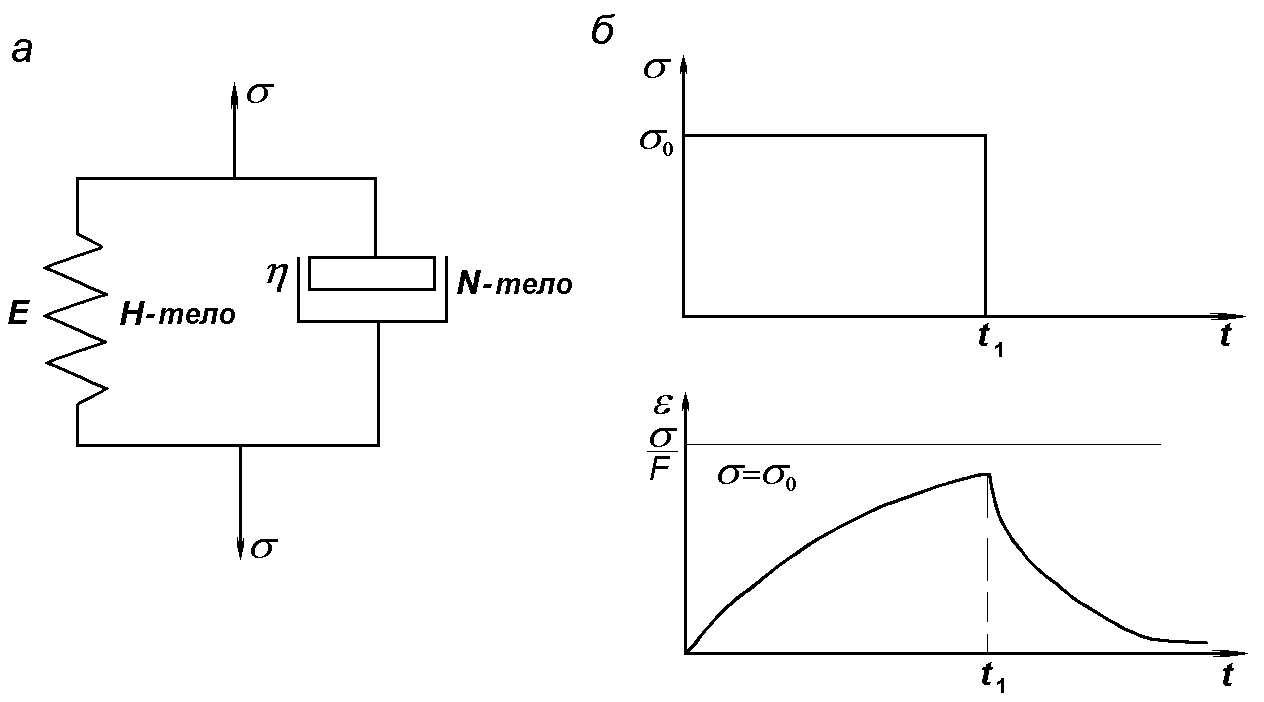
Рис. 1.2. Условная схема (а) и реологическое поведение тела Гука (б)

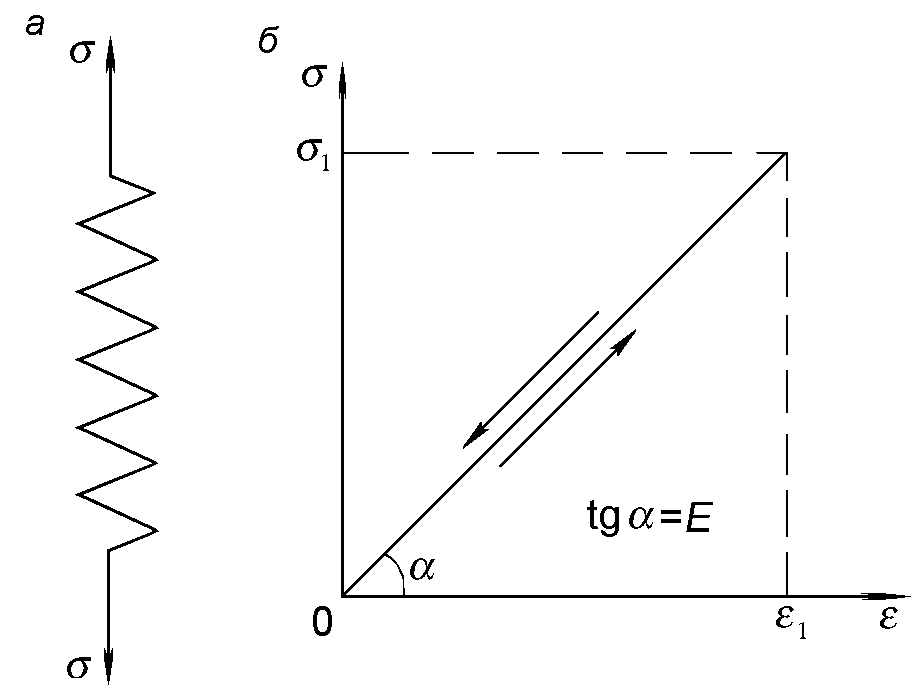
У тела Гука напряжение прямо пропорционально относительной деформации, т.е.

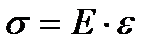, (1.3)

где E – модуль упругости тела;

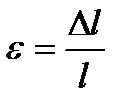– относительная деформация при растяжении или сжатии;

l – начальная длина тела;

Δl – абсолютная деформация (удлинение или сокращение длины) тела при растяжении или сжатии.

Графически зависимость σ от ε показана на рис. 1.2, б.

При приложении нагрузки деформация тела 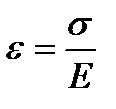развивается мгновенно и так же мгновенно полностью снимается при снятии нагрузки (при разгрузке).

При снятии нагрузки тело принимает исходные размеры. Напряжения, возникающие в теле, являются временными. При снятии нагрузки они исчезают.

При чистом сдвиге закон Гука имеет вид

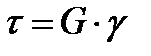, (1.4)

где γ – относительная деформация при сдвиге;

G – модуль упругости при сдвиге.

Схема чистого сдвига приведена на рис. 1.3.

Как следует из рис. 1.3, .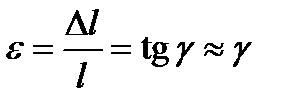

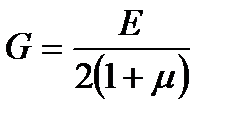, (1.5)

где μ – коэффициент Пуассона, равный отношению удлинения к поперечному сжатию образца при растяжении. Для стали и алюминия коэффициент Пуассона соответственно равен 0,24÷0,28 и 0,3÷0,33.

Упругое тело Гука является основной моделью механического поведения твердых тел. Твердые тела с некоторым приближением подчиняются закону Гука, пока развиваемые напряжения не превзойдут некоторой величины, называемой пределом текучести (σ_т или τ_s). Если напряжения превысят значение σ_т или τ_s, то будет происходить пластическая деформация. Если пластическая деформация не сопровождается упрочнением материала (идеальная пластичность), то мы имеем реологическое тело Сен-Венана. Схема такого тела приведена на рис. 1.4.

Если развиваемое приложенными усилиями касательное напряжение τ меньше величины предельного касательного напряжения сдвига τ_s, то деформация тела отсутствует (γ=0).

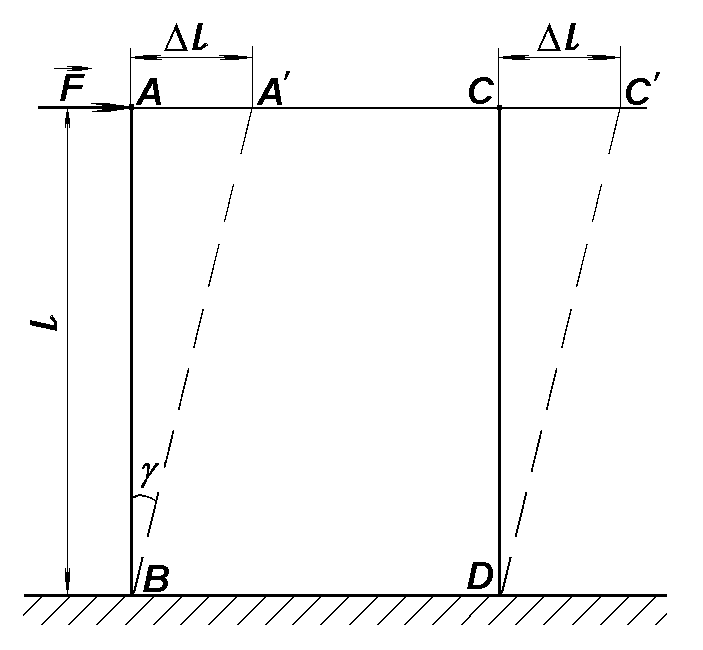
Рис. 1.3. Схема чистого сдвига

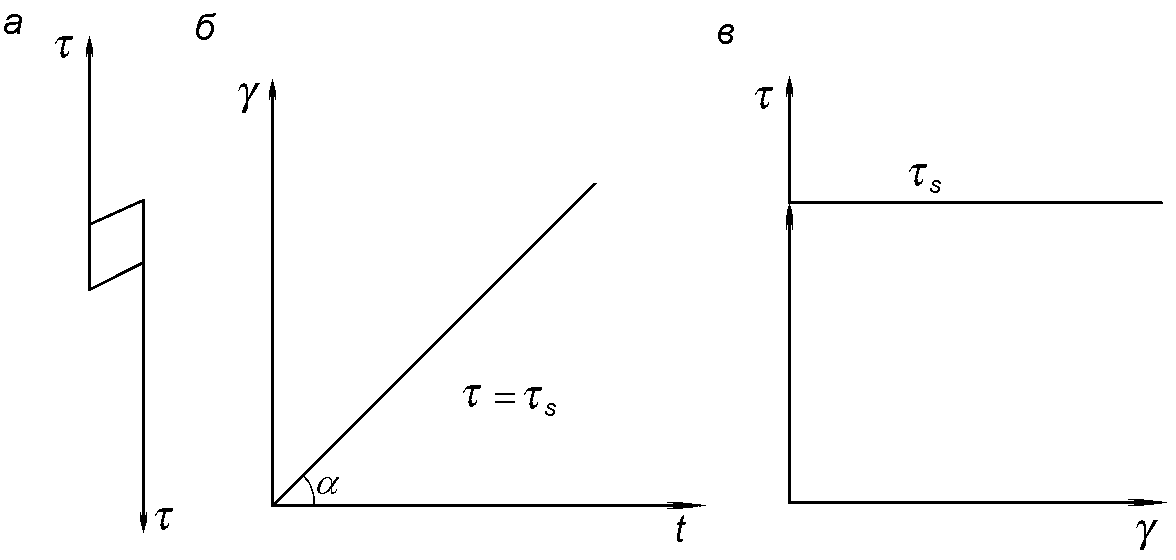
Рис.1.4. Схема (а) и реологическое поведение тела Сен-Венана при τ=τs (б) и τ<τs (в)

При τ=τ_s дальнейший рост напряжения прекращается, а деформация тела γ развивается в соответствии с движением деформирующего тело пуансона.

Простейшей моделью механического поведения жидкостей является тело Ньютона, или ньютоновская жидкость (N-тело). В соответствии с законом Ньютона касательные напряжения пропорциональны градиенту скорости.

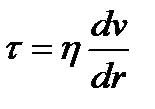, (1.6)

где η – динамический коэффициент вязкости;

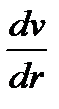– градиент скорости.

Как видно на рис. 1.3,

,

,

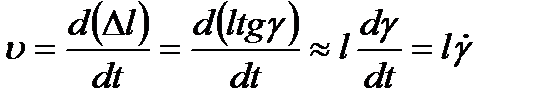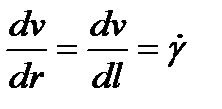где 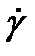– скорость деформации.

С учетом этого реологический закон тела Ньютона принимает вид

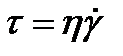. (1.7)

В отличие от Н-тела у N-тела напряжение пропорционально не деформации 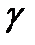, а скорости ее изменения 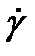. Определим деформацию N-тела при постоянном напряжении τ=const. Из (1.7) следует 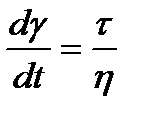. Отсюда имеем

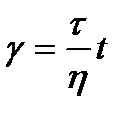. (1.8)

Из (1.8) видно, что деформация 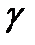увеличивается пропорционально времени и тем быстрее, чем больше отношение 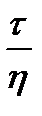. При снятии напряжения деформация не исчезает, а остается равной 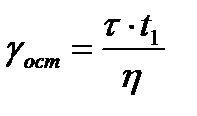, где t₁ – время, за которое была снята нагрузка.

Таким образом, в отличие от Н-тела деформация N-тела является остаточной. Из уравнения (1.7) следует, что если γ=const, то τ=0. Поэтому в покоящейся жидкости касательные напряжения τ развиваться не могут. Появление любых, как угодно малых, касательных усилий приводит к растеканию жидкости.

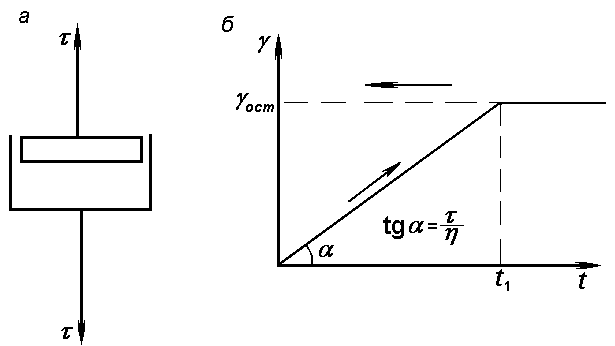
Рис. 1.5. Схема N-тела (а) и зависимость деформации тела Ньютона от времени (б)

На рис. 1.5 приведено условное обозначение N-тела, а также характер изменения его деформации при τ=const.

Рассмотренные элементарные реологические тела Гука, Сен-Венана и Ньютона являются базовыми для составления реологических схем реальных тел. Эти схемы образуются последовательным и параллельным соединением указанных базовых элементов.

При описании поведения составных тел необходимо руководствоваться следующими правилами:

– при последовательном соединении элементов напряжения, развиваемые во всех элементах, одинаковы, а для деформации справедливо уравнение

,

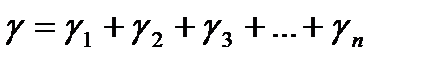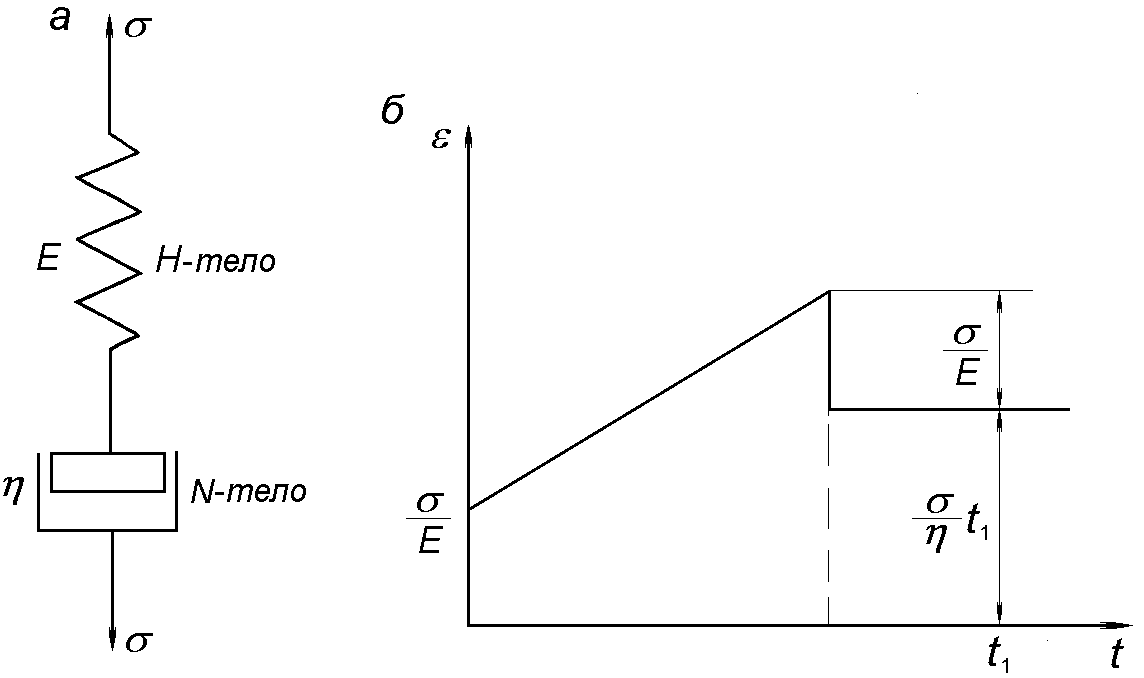
где 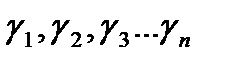– деформации последовательно соединенных элементов;

– при параллельном соединении элементов их деформации одинаковы, а сумма напряжений, развиваемых в элементах, равна напряжению, развиваемому приложенными к телу усилиями.

Рассмотрим описание реологического поведения ряда сложных тел.

Тело Максвелла (М-тело)

Рис. 1.6. Схема тела Максвелла (а) и изменение его деформации при σ = const (б)

Тело Максвелла представляет собой последовательно соединенные тела Гука и Ньютона (рис. 1.6, а).

Деформация тела Максвелла равна сумме деформаций тела Гука (ε₁) и тела Ньютона (ε₂), т.е. .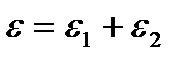

; ; ;

; .

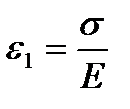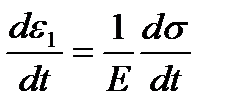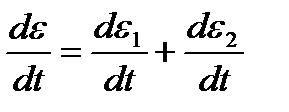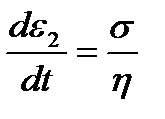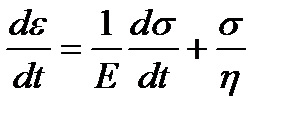Основное реологическое уравнение тела Максвелла можно записать следующим образом:

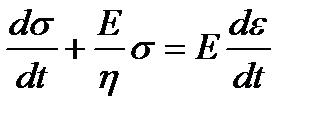. (1.9)

Решим уравнение (1.9) для двух частных случаев: σ=const и ε=const.

При постоянном напряжении (σ=const) 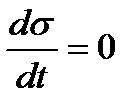и (1.9) принимает вид 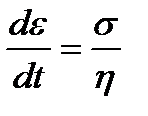. Отсюда .

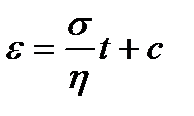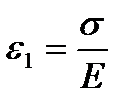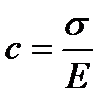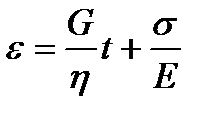При t=0 тело Гука мгновенно деформируется на величину , а деформация тела Ньютона при t=0 ε₂=0. С учетом этого находим и . При t=t₁ 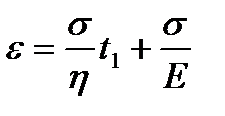. Если в момент t=t₁ разгрузить тело, т.е. выполнить следующее условие: при t>t₁ σ=0, то упругая деформация 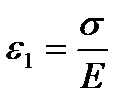исчезнет и останется остаточная деформация .

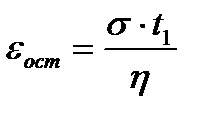При постоянной деформации, т.е. при ε=ε₀=const, уравнение (1.9) принимает вид

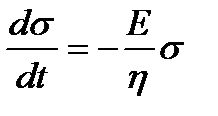, или .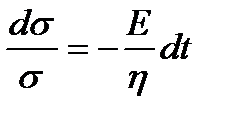

Интегрируя это уравнение, получаем

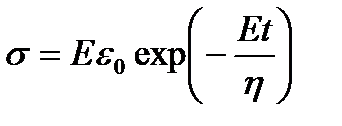. (1.10)

Из (1.10) видно, что напряжение монотонно убывает со временем, стремясь к нулю при .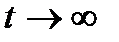

Процесс уменьшения напряжения при ε=const называется релаксацией напряжений. Уменьшение напряжений вызывается переходом упругой деформации тела Гука в пластическую деформацию тела Ньютона. При этом происходит постепенная разгрузка тела Гука.

Время 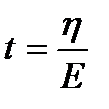называется временем релаксации. За время, равное времени релаксации, напряжение уменьшается в ε раз.

По механическому поведению к телу Максвелла близки сплавы в нижней, примыкающей к температуре солидуса, части интервала кристаллизации.

Тело Кельвина (К-тело)

Рис. 1.7. Схема тела Кельвина (а) и зависимость его деформации от времени при σ=const (б)

Тело Кельвина представляет собой систему параллельно соединенных тел Ньютона и Гука (рис. 1.7). Напряжение σ равно сумме напряжений в теле Ньютона – σ₁ и в теле Гука – σ₂: 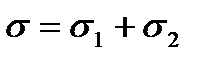; 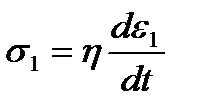и 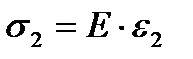.Так как элементы соединены параллельно, то их деформации равны, т.е. 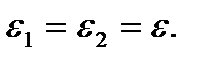С учетом этих выражений получаем дифференциальное реологическое уравнение тела Кельвина.

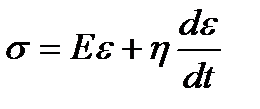, или 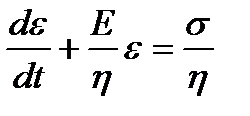. (1.11)

При σ=const уравнение (1.11) – линейное дифференциальное уравнение первого порядка с постоянной правой частью.

Примем , .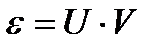

; ; ;

; ; .

; ;

.

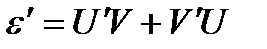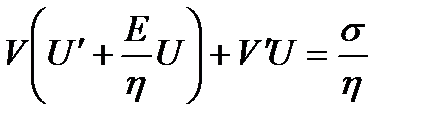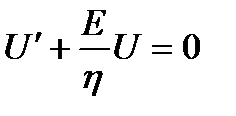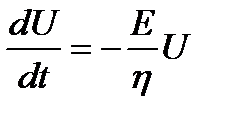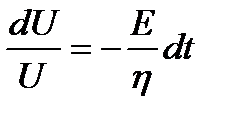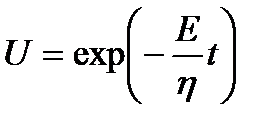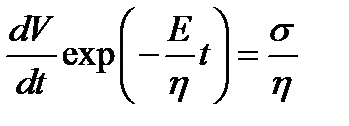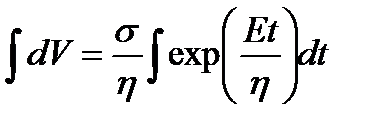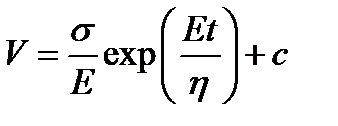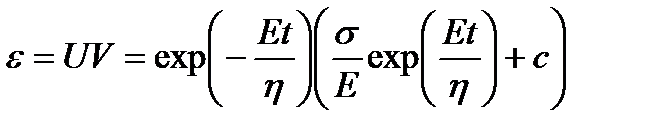Мгновенное приложение нагрузки при t=0 не может вызвать соответствующую деформацию тела Гука, так как параллельно соединенное с ним тело Ньютона не дает ему мгновенно деформироваться. Поэтому ε=0 при t=0. С учетом этого имеем 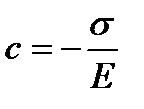. Тогда

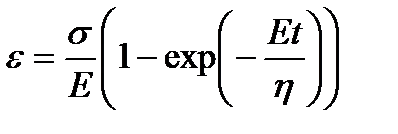. (1.12)

Из (1.12) видно, что с ростом времени ε монотонно растет, стремясь к 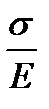при t . Если при t=t₁ снять нагрузку, то деформация будет монотонно уменьшаться, стремясь к нулю.

Так как мгновенная деформация тела Кельвина невозможна, решение по (1.11) при 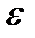=const не проводится.

Тело Бингама (В-тело)

Тело Бингама представляет собой совокупность параллельно соединенных тел Сен-Венана и Ньютона (рис. 1.8).

Рис. 1.8. Схема тела Бингама (а) и изменение деформации тела Бингама (б) при τ = const

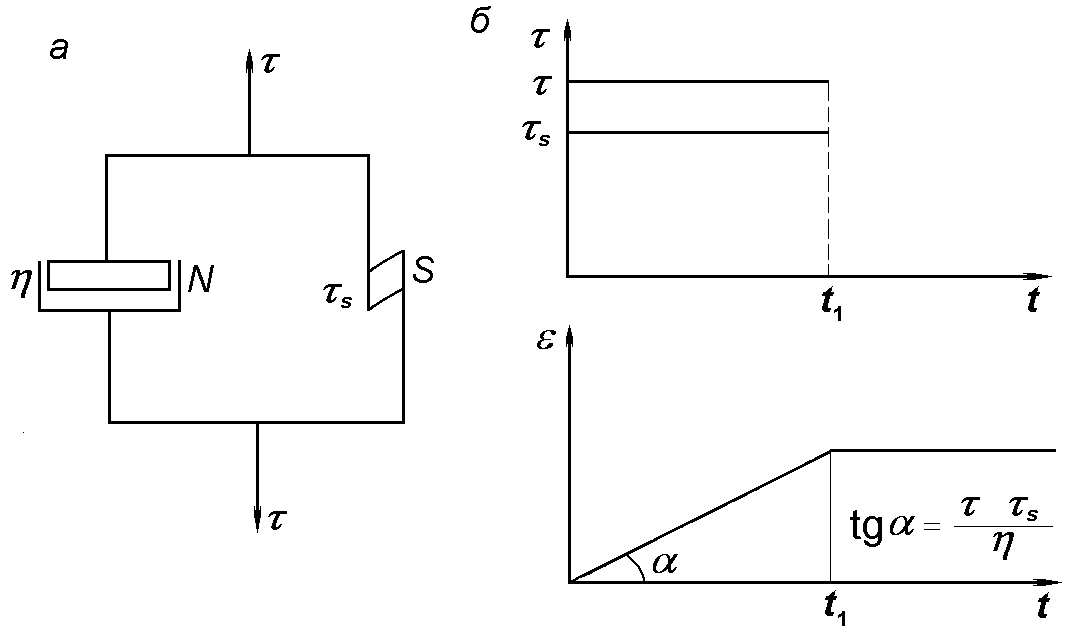
При τ<τ_s скорость деформации тела Сен-Венана равна нулю. Поэтому равна нулю и скорость деформации тела Ньютона, а также всего тела Бингама.

При τ 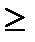τ_s напряжение тела Сен-Венана равно τ_s, а напряжение тела Ньютона – τ_N=τ–τ_s. Тогда реологический закон тела Бингама имеет вид

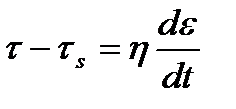^, или 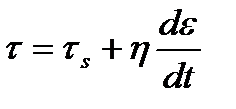. (1.13)

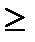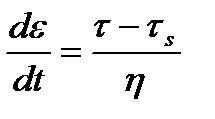При τ<τ_s ε=0. При τ τ_s , или 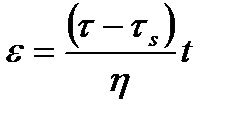. При t=t₁ в теле будет остаточная деформация .

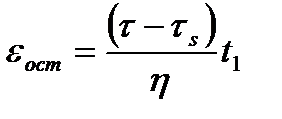По типу тела Бингама ведут себя вязкопластические жидкости, к которым относятся концентрированные суспензии. К этим же телам можно отнести сплавы внутри интервала кристаллизации вблизи температуры ликвидуса. В этом случае сплавы представляют собой суспензию, количество твердой фазы в которой для бинарных сплавов можно определить по правилу рычага. Величина предельного касательного напряжения τ_s и структурная вязкость η зависят от количества и формы выделений твердой фазы. При некотором количестве твердой фазы, соответствующем температуре нулевой жидкотекучести, напряжения, развиваемые активными силами, движущими поток сплава в форме, становятся меньше τ_s. При этом происходит остановка потока сплава.

Тело Шведова (Sch-тело)

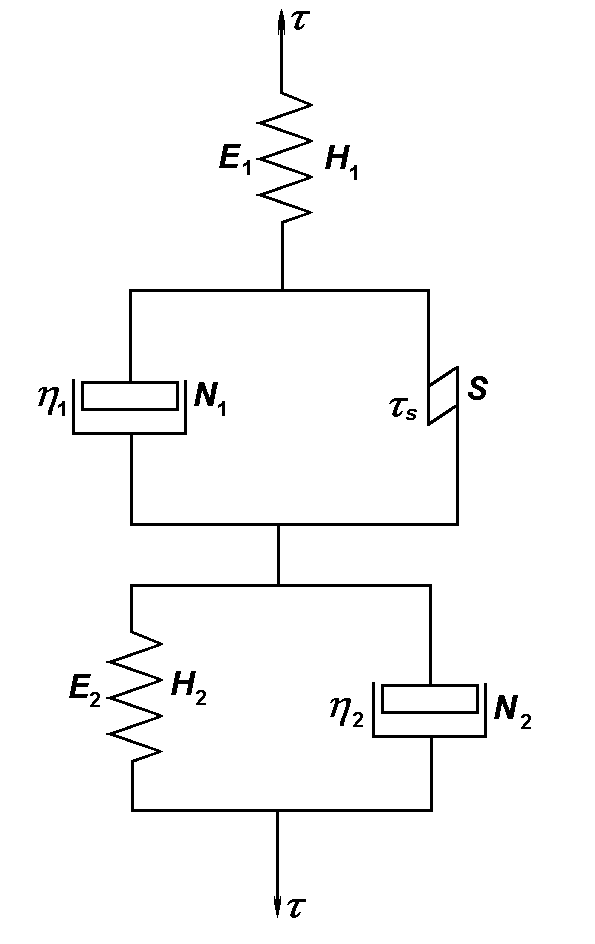
Рис. 1.9. Схема тела Шведова

В исследованиях Г.Ф. Баландина и Л.П. Каширцева показано, что реологическое поведение сплавов в широком интервале температур может быть описано моделью тела Шведова, представляющего собой комбинацию тел Гука, Бингама и Кельвина (рис. 1.9).

Поведение сплава описывается пятью реологическими характеристиками: E₁, E₂, η₁, η₂ и τ_s, которые изменяются в зависимости от температуры. Реологические свойства алюминиево-кремниевого сплава и основные зависимости реологической модели тела Шведова рассматриваются в п. 4.3 в в связи с анализом напряжений и деформаций в отливках.