Дополнительные точки, если нет асимптот.

Построение графика.

Область значения функции.

Неопределенный интеграл, его свойства. Методы вычисления неопределенного интеграла: непосредственное интегрирование. Примеры.

Множество всех первообразных для функции f(x) на промежутке Х называется неопределенным интегралом от функции f(x)

Свойства:

1) Производная от неопределенного интеграла равна подынтегральной функции:

2) Дифференциал неопределенного интеграла равен подынтегральному выражению:

D ( ∫ f(x)dx)=f(x)dx

3) Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого С:

∫ df(x)=f(x)+C

Постоянный множитель можно выносить за знак интеграла

∫ kf(x)dx=k∫f(x)dx

5) Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций:

∫(f(x)+g(x))dx=∫f(x)dx+∫g(x)dx

Пусть функция f(x) имеет первообразную F(x), тогда

∫f(kx+b)dx= F(kx+b)+C

Методы вычисления неопределенного интеграла:

1) Метод непосредственного интегрирования ( основан на применении свойств интеграла)

∫(1-sinx)dx=∫dx -∫sinxdx=x+cos+C

Метод замены переменной ( основан на понятии производной сложной функции)

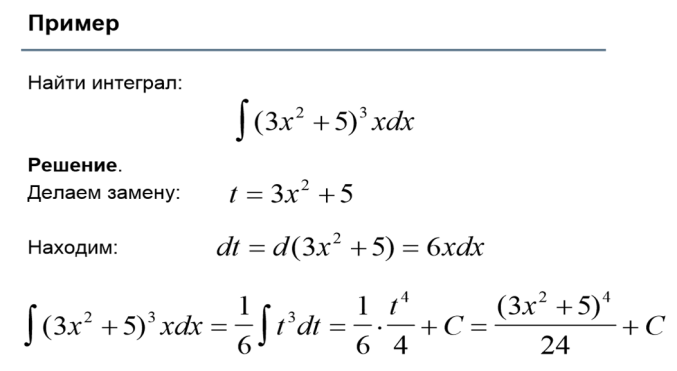
3) Метод интегрирования по частям (по формуле ∫udv=uv-∫udu)

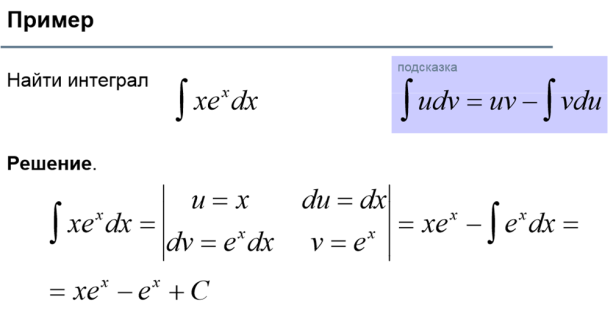
Методы вычисления неопределенного интеграла: интегрирование методом подстановки. Примеры.

Основан на применении свойств интеграла F( 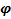(x))

Если функция f(t) имеет первооборазнуюF(t), а функция t= 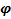(x) дифференцируема, то функция f(φ(x)) также имеет первообразную:

∫ f(φ(x))d(φ(x))-F(φ(x)+C

Определенный интеграл, его свойства и смысл.

Определенным интегралом от функции f(x) на отрезке [a; b] называется предел интегральной суммы 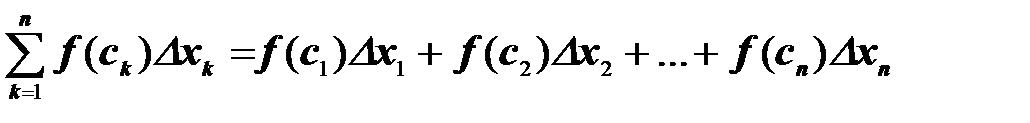, при условии, что длина наибольшего из элементарных отрезков стремится к нулю:

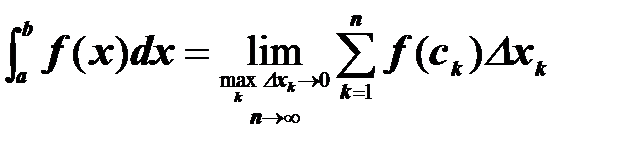
Свойства определенного интеграла

Определенный интеграл не зависит от обозначения переменной интегрирования, т.е.

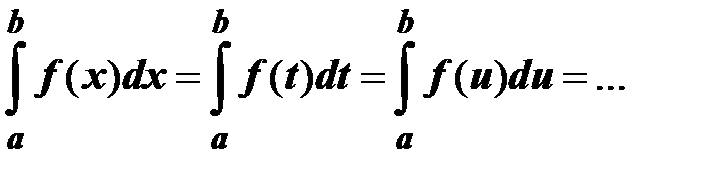
2.

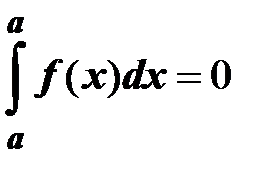
3. Определенный интеграл от суммы конечного числа непрерывных функций f1(x), f2(x), …, fn(x), заданных на отрезке [a; b], равен сумме определенных интегралов от этих функций:

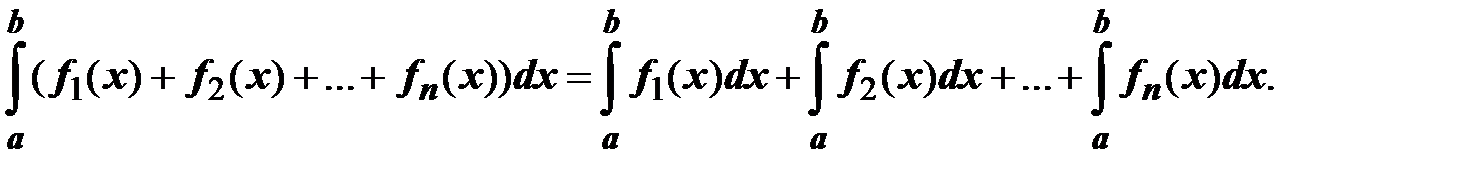
4. Постоянный множитель можно выносить за знак определенного интеграла:

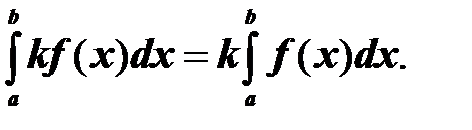
5.

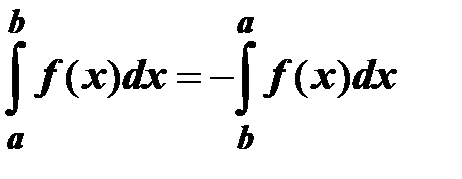
6. , где a < c < b.

7. Если f(x) 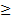0 на отрезке [a; b], то 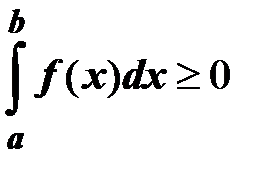; если f(x) 0 на отрезке [a; b], то

8. Если m, M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a; b]: m f(x) ≤M, то .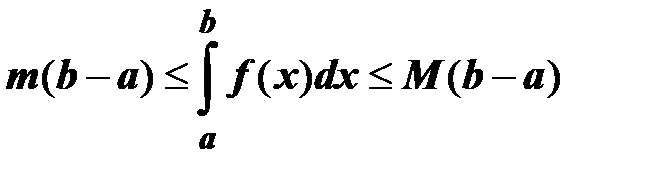

9. Если f(x) ≤ g(x) на отрезке [a; b], то .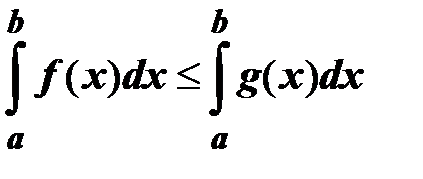

10. Определенный интеграл от непрерывной функции равен произведению значения этой функции в некоторой промежуточной точке х=с отрезка интегрирования [a; b] на длину этого отрезка (теорема о среднем):

или .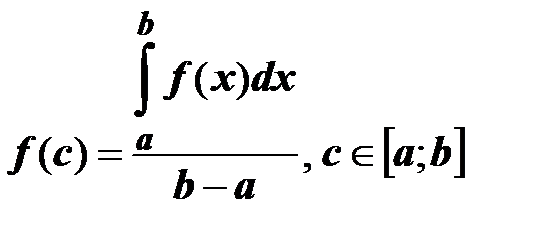

11. .

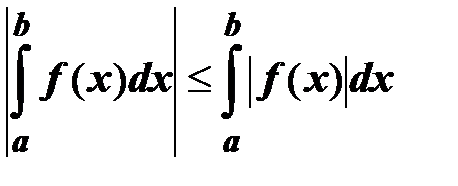12. .

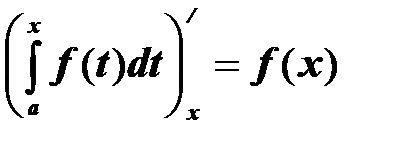Смысл определенного интеграла:

Геометрический смысл определенного интеграла. представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f(x)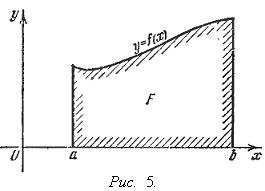

Методы вычисления определенного интеграла: непосредственное