Программа 1. Корень уравнения

#include<iostream>#include <cmath>usingnamespacestd;constdouble epsilon = 1e-2; double f(double x){return4-exp(x)-2*x^2;} int main(){double a, b, c; a =0; b =2;while(b - a > epsilon){ c =(a + b)/2;if(f(b)* f(c)<0) a = c;else b = c;}cout<<(a + b)/2<<endl;return0;}

Искомый корень 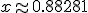. Вычисления проводились с точностью .

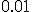Промежуточные вычисления представлены в таблице ниже.

n	an	bn	cn	bn-cn
			0.5	0.5
	0.5		0.75	0.25
	0.75		0.875	0.125
	0.875		0.9375	0.0625
	0.875	0.9375	0.90625	0.03125
	0.875	0.90625	0.890625	0.015625
	0.875	0.890625	0.8828125	0.0078125

Достоинство метода половинного деления : более быстрая сходимость к заданной точности, чем у шагового. Недостаток: если на отрезке [а,b] содержится более одного корня, то метод не работает.

8. Численное решение уравнения методом хорд. Эффективность данного алгоритма. Привести фрагмент программы,поясняющий данный алгоритм.

Метод хорд

Метод основан на замене функции f(x) на каждом шаге поиска хордой, пересечение которой с осью Х дает приближение корня.

При этом в процессе поиска семейство хорд может строиться:

а) при фиксированном левом конце хорд, т.е. z=a, тогда начальная точка х₀=b (рис. 4.10а);

б) при фиксированном правом конце хорд, т.е. z=b, тогда начальная точка х₀=a (рис. 4.10б);

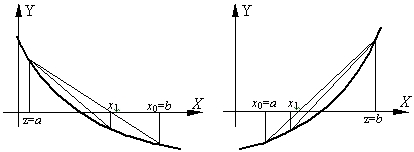
Рис. 4.10.

В результате итерационный процесс схождения к корню реализуется рекуррентной формулой:

для случая а)

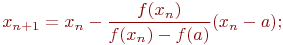(4.11)

для случая б)

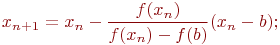(4.12)

Процесс поиска продолжается до тех пор, пока не выполнится условие

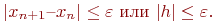(4.13)

Метод обеспечивает быструю сходимость, если f(z)f"(z) > 0, т.е. хорды фиксируются в том конце интервала [a,b], где знаки функции f(z) и ее кривизны f"(z) совпадают.

Схема алгоритма уточнения корня методом хорд

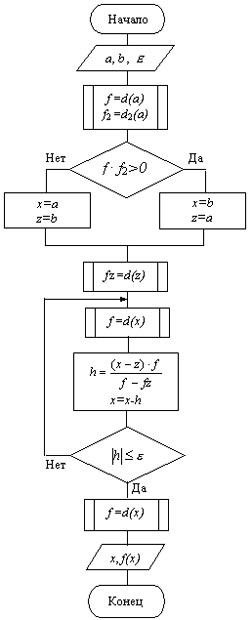
Пример программы:

double f(double x)

{

returnsqrt(fabs(cos(x)))- x;// Заменить ф-ей, корни которой мы ищем

}

// a, b - пределы хорды, epsilon - необходимая погрешность

doublefindRoot(double a,double b,double epsilon)

{

while(fabs(b - a)> epsilon)

{

a = b -(b - a)*f(b)/(f(b)- f(a));

b = a -(a - b)*f(a)/(f(a)- f(b));

}

// a - i-1, b - i-тыйчлены

return b;

}

Численное решение уравнения методом Ньютона (касательных). Эффективность данного алгоритма. Привести фрагментпрограммы, поясняющий данный алгоритм.

Метод Ньютона (метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции.

Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации.

Метод обладает квадратичной сходимостью.

Геометрический смысл метода Ньютона состоит в том, что на каждом шаге мы строим касательную к графику 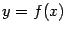в точке очередного последовательного приближения Xn, а за следующее приближение Xn+1 берём точку пересечения этой касательной с осью 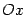. Тем самым наклон прямой подстраивается на каждом шаге наилучшим образом.

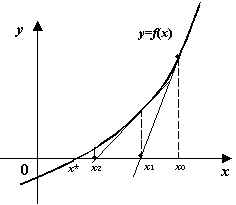
Значение корня новой итерации вычисляется по формуле

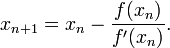
Алгоритм

1. Задается начальное приближение x₀.

2. Пока не выполнено условие остановки, в качестве которого можно взять 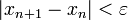или 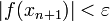(то есть погрешность в нужных пределах), вычисляют новое приближение: 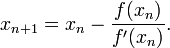[1].

Достоинства метода Ньютона: Метод Ньютона - самый быстрый способ нахождения корней уравнений: обычно заданная точность достигается за 2-3 итерации. Очень быстрая сходимость по сравнению с методом половинного деления и методом простой итерации к заданной точности.

Недостаток: громоздкий алгоритм: на каждой итерации необходимо вычислять значение функции и ее первой производной.