Базис и ранг системы векторов

СИСТЕМА ВЕКТОРОВ

1.1.Разложение вектора по системе векторов

Векторk₁a₁ + k₂a₂ + … + k_na_nназывается линейной комбинацией векторов

a₁, a₂, … , a_nскоэффициентамиk₁, k₂, … , k_n .

Вектор bлинейно выражается через векторы a₁, a₂, … , a_n,если

b = k₁a₁ + k₂a₂ + … + k_na_n .

В этом случае говорят также, что bразлагается по векторам a₁, a₂, … , a_n. Каждый

n-мерный вектор b = { b₁, b₂, … , b_n } однозначно разлагается по диагональной системе

e₁ = {1, 0, … , 0},

e₂ = {0, 1, … , 0},

. . . . . . . . . . . . . .

e_n = {0, 0, … , 1}

с коэффициентами, которые равны координатам вектора b:

b = b₁e₁ + b₂e₂ + … + b_ne_n.

Чтобы найти разложение вектора b по системе векторов a₁, a₂, … , a_nдостаточно найти какое-нибудь решение системы уравнений

a₁x₁ + a₂x₂ + … + a_nx_n= b.

Пример.

Выяснить, разлагается ли вектор b по системе векторов a₁, a₂, … , a_n:

b = { 2, 7, 17 , 0}, a₁ = { 2, 4, 3 , 0}, a₂ = { –3, 0, 1 , 3}, a₃ = { 1, –1, 10, –3}.

Р е ш е н и е.Ищем общее решение системы уравнений

a₁x₁ + a₂x₂ + a₃ x₃= b

методомГаусса. Для этого запишем эту систему по координатам:

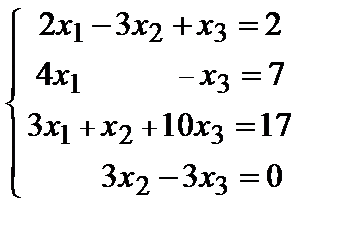
Расширенная матрица системы

~ ~

~ ~ ~ .

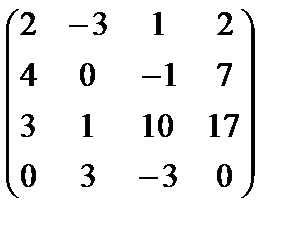
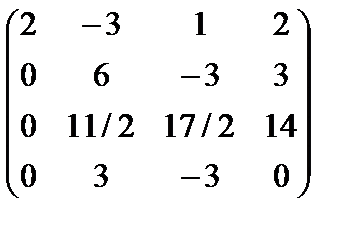
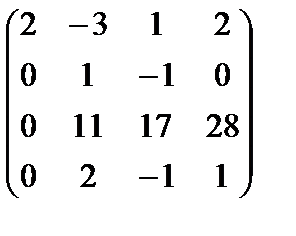
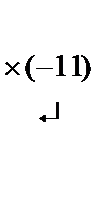
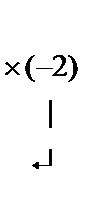
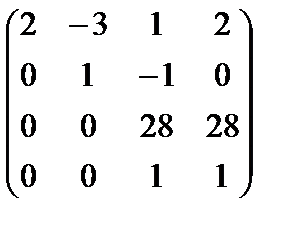
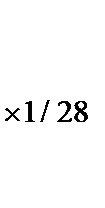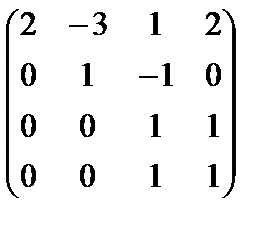
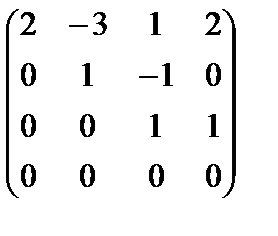Разрешенная система имеет вид: 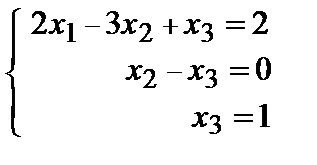(r_A = r_A|B = 3, n = 3).

Система определена: х₃ = 1, х₂ = 1, х₁ = 2.

Следовательно, b= 2a₁+ a₂+ a₃.

Задания.Выяснить, разлагается ли вектор b по системе векторов a₁, a₂, … , a_n :

1. b = { 2, 2, 3 , 3}, a₁ = { 1, 2, 3 , 1}, a₂ = { 2, 1, 2 , 3}, a₃ = { 3, 2, 4, 4}.

2. b = { 4, 1, 3 , 1}, a₁ = { 2, 0, 1 , 1}, a₂ = { 1, 1, 2 , -2}, a₃ = { 2, 1, 3, -3 }.

3. b = { -1, 1, 3 , 1}, a₁ = { 1, 2, 1 , 1}, a₂ = { 1, 1, 1 , 2}, a₃ = { -3, -2, 1, -3}.

4. b = { 1, 0, 0 , 1}, a₁ = { 2, 1, 1 , 3}, a₂ = { 3, 0, -1 , 2}, a₃ = { 1, -1, 0,1},

a₄ = { 1, 0, -2, -1 }.

5. Показать, что ни один из векторов диагональной системы не разлагается по остальным ее векторам.

6. Вектор b разлагается по системе векторов a₁, a₂, … , a_m . Доказать, что каждый вектор системы b+a₁, b+a₂, … , b+a_m разлагается по системе a₁, a₂, … , a_m .

1.2.Линейная зависимость

Система векторов a₁, a₂, … , a_nназывается линейно зависимой, если можно подобрать такие числа k₁, k₂, … , k_n , не все равные нулю, что

k₁a₁ + k₂a₂ + … + k_na_n = Θ, гдеΘ = {0, 0, … , 0}.

Система векторов a₁, a₂, … , a_nназывается линейно независимой, если из каждого соотношения вида k₁a₁ + k₂a₂ + … + k_na_n = Θследует

k₁=k₂= … =k_n=0.

Система векторов линейно зависима тогда и только тогда, когда система уравнений

a₁x₁ + a₂x₂ + … + a_nx_n= Θ

имеет ненулевое решение. Система векторов линейно н е зависима тогда и только тогда, когда система уравнений a₁x₁ + a₂x₂ + … + a_nx_n= Θимеет только нулевое решение.

Вектор b разлагается по линейно независимой системе a₁, a₂, … , a_n тогда и только тогда, когда a₁, a₂, … , a_n, b – линейно зависимая система векторов.

Система векторов линейно зависима, если количество координат у векторов системы меньше, чем векторов в системе.

Если каждый вектор системы b₁, b₂, … , b_n разлагается по векторам a₁, a₂, … , a_m и n>m, то b₁, b₂, … , b_n – линейно зависимая система векторов.

Пример 1.

Выяснить, является ли данная система векторов линейно зависимой или линейно независимой:

a₁ = { 3, 5, 1 , 4}, a₂ = { –2, 1, -5 , -7}, a₃ = { -1, –2, 0, –1}.

Р е ш е н и е.Ищем общее решение системы уравнений

a₁x₁ + a₂x₂ + a₃ x₃= Θ

методомГаусса. Для этого запишем эту однородную систему по координатам:

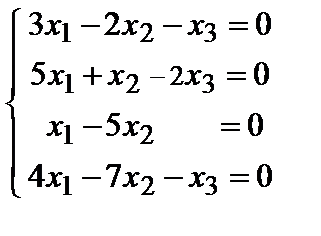
Матрица системы

~ ~ ~ .

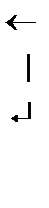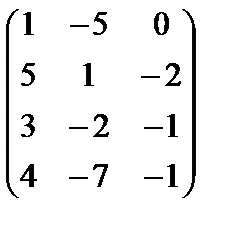
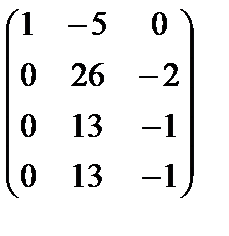
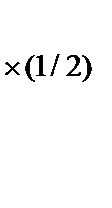
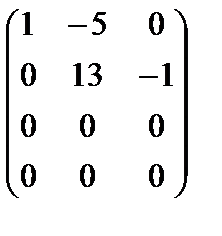Разрешенная система имеет вид: 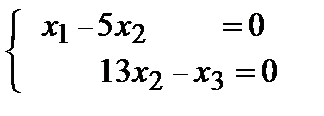(r_A = 2, n = 3). Система совместна и неопределена. Ее общее решение (x₂– свободная переменная ): x₃ = 13x₂;x₁=5x₂ =>

=>X_o = 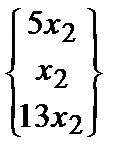.Наличие ненулевого частного решения, например, 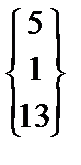, говорит о том, векторы a₁, a₂, a₃ линейно зависимы.

Пример 2.

Выяснить, является ли данная система векторов линейно зависимой или линейно независимой:

1. a₁ = { -20,-15, -4}, a₂ = { –7, -2, -4}, a₃ = { 3, –1, –2}.

Р е ш е н и е.Рассмотрим однородную систему уравнений a₁x₁ + a₂x₂ + a₃x₃ = Θ

или в развернутом виде (по координатам)

Система однородна. Если она невырождена, то она имеет единственное решение. В случае однородной системы – нулевое (тривиальное) решение. Значит, в этом случае система векторов независима. Если же система вырождена, то она имеет ненулевые решения и, следовательно, она зависима.

Проверяем систему на вырожденность:

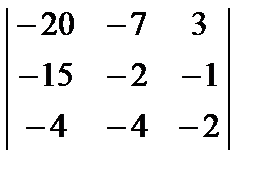= –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.

Система невырождена и ,т.о., векторы a₁, a₂, a₃ линейно независимы.

Задания.Выяснить,является ли данная система векторов линейно зависимой или линейно независимой:

1. a₁ = { -4, 2, 8}, a₂ = { 14, -7, -28}.

2. a₁ = { 2, -1, 3, 5}, a₂ = { 6, -3, 3, 15}.

3. a₁ = { -7, 5, 19}, a₂ = { -5, 7 , -7}, a₃ = { -8, 7, 14}.

4. a₁ = { 1, 8 , -1}, a₂ = { -2, 3, 3}, a₃ = { 4, -11, 9}.

5. a₁ = {0, 1, 1 , 0}, a₂ = {1, 1 , 3, 1}, a₃ = {1, 3, 5, 1}, a₄ = {0, 1, 1, -2}.

6. Доказать, что система векторов будет линейно зависимой, если она содержит:

а) два равных вектора;

б) два пропорциональных вектора.

7. Ненулевой вектор b разлагается по системе a₁, a₂, a₃ и по системе a₄, a₅, a₆. Доказать,

что a₁, a₂, a₃,a₄, a₅, a₆ линейно зависимая система векторов.

8. Доказать, что векторы a₂-a₁, a₃-a₁ не пропорциональны, если a₁, a₂, a₃– линейно

независимые векторы.

Пример.

Найти базис системы векторов и векторы, не входящие в базис, разложить по базису:

а₁={5, 2, -3, 1}, а₂={4, 1, -2, 3}, а₃={1, 1, -1, -2}, а₄={3, 4, -1, 2}, а₅={13, 8, -7, 4}.

Р е ш е н и е. Рассмотрим однородную систему линейных уравнений

а₁х₁ +а₂х₂ +а₃х₃ +а₄х₄ +а₅х₅= 0

или в развернутом виде .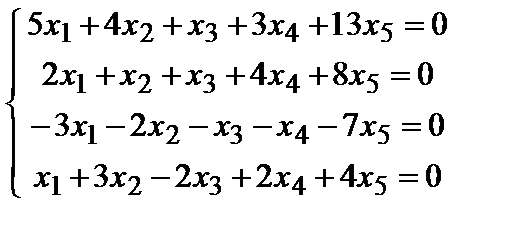

Будем решать эту систему методом Гаусса, не меняя местами строки и столбцы, и, кроме того, выбирая главный элемент не в верхнем левом углу, а по всей строке.Задача состоит в том, чтобы выделить диагональную часть преобразованной системы векторов.

~ ~

~ ~ ~ .

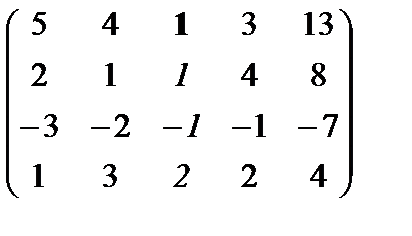
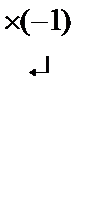
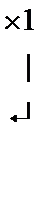
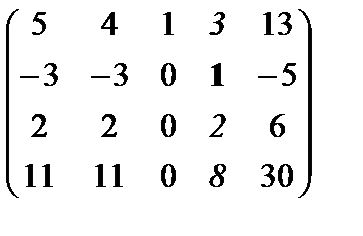
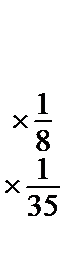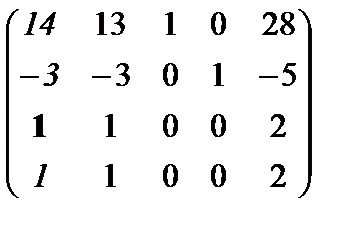
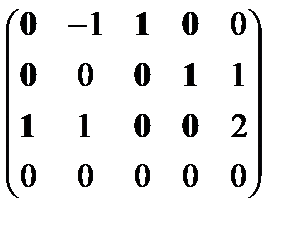Разрешенная система векторов, равносильная исходной, имеет вид

а₁¹х₁ +а₂¹х₂ +а₃¹х₃ +а₄¹х₄ +а₅¹х₅= 0,

где а₁¹= 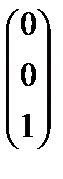, а₂¹= 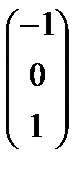, а₃¹= 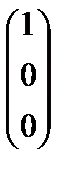, а₄¹= 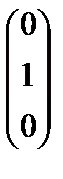, а₅¹= 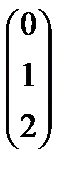. (1)

Векторы а₁¹,а₃¹, а₄¹образуют диагональную систему. Следовательно, векторы а₁,а₃, а₄ образуют базис системы векторов а₁,а₂, а₃, а₄, а₅.

Разложим теперь векторы а₂иа₅ по базису а₁,а₃, а₄. Для этого сначала разложим соответствующие векторы а₂¹иа₅¹ по диагональной системеа₁¹,а₃¹, а₄¹, имея в виду, что коэффициентами разложения вектора по диагональной системе являются его координаты x_i.

Из (1) имеем:

а₂¹= а₃¹· (-1) + а₄¹· 0 + а₁¹·1 =>а₂¹= а₁¹ –а₃¹.

а₅¹= а₃¹· 0 + а₄¹· 1 + а₁¹·2 =>а₅¹= 2а₁¹ +а₄¹.

Векторы а₂иа₅ разлагаются по базису а₁,а₃, а₄ с теми же коэффициентами, что и векторы а₂¹иа₅¹ по диагональной системе а₁¹,а₃¹, а₄¹ (те коэффициенты x_i). Следовательно,

а₂= а₁ –а₃, а₅= 2а₁ +а₄.

Задания. 1.Найти базис системы векторов и векторы, не входящие в базис, разложить по базису:

1. a₁ = { 1, 2, 1}, a₂ = { 2, 1, 3}, a₃ = { 1, 5, 0 }, a₄ = { 2, -2, 4}.

2. a₁ = { 1, 1, 2}, a₂ = { 0, 1, 2}, a₃ = { 2, 1, -4 }, a₄ = { 1, 1, 0}.

3. a₁ = { 1, -2, 3}, a₂ = { 0,1, -1}, a₃ = { 1, 3, 0}, a₄ = { 0, -7, 3 }, a₅ = { 1, 1, 1}.

4. a₁ = { 1, 2, -2}, a₂ = { 0, -1, 4}, a₃ = { 2, -3,3 }.

2.Найти все базисы системы векторов:

1. a₁ = { 1, 1, 2}, a₂ = { 3, 1, 2}, a₃ = { 1, 2, 1 }, a₄ = { 2, 1, 2}.

2. a₁ = { 1, 1, 1}, a₂ = { -3, -5, 5}, a₃ = { 3, 4, -1 }, a₄ = { 1, -1, 4}.

Пример.

Применяя процесс ортогонализации, построить ортогональную систему векторов:

а₁={2, 0, 1, 1}, а₂={1, 2, 0, 1}, а₃={0, 1, -2, 0}.

Р е ш е н и е. Полагаем b₁ = a₁. Затем строим векторы b₂ и b₃.

b₂ = a₂ – 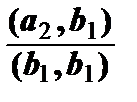b₁ = {1, 2, 0, 1} – 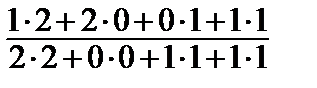·{2, 0, 1, 1} = {1, 2, 0, 1} – 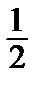·{2, 0, 1, 1} =

= {0, 2, – , };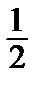

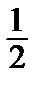b₃ = a₃ – 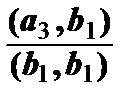b₁– 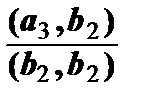b₂ = {0, 1, -2, 0} – 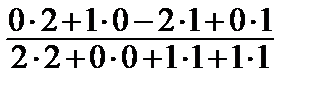·{2, 0, 1, 1}–

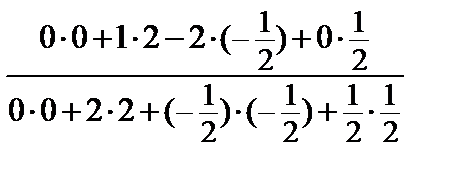– ·{0, 2, – 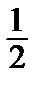, 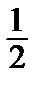}= {0, 1, -2, 0} – (– 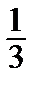) ·{2, 0, 1, 1}– 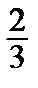·{0, 2, – , }=

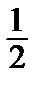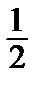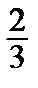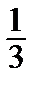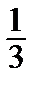= {0, 1, -2, 0} +{ , 0, 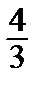, 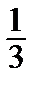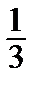}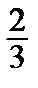–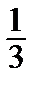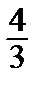{0, , – , }={ , – , – , 0}.

Т.о., векторыb₁ = {2, 0, 1, 1}, b₂ = {0, 2, – 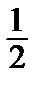, 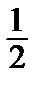}, b₃ = { 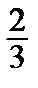, – , – 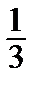, 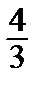0} являются результатом ортогонализации исходной системы векторов.

Задания. 1.Применяя процесс ортогонализации, построить ортогональную систему векторов:

1. {0, 1, 1}, {1, 1, 1}, {-3, 3, 1}.

2. {1, -1, 1}, {2, 1, 2}, {3, 1, 1}.

3. {1, -2, 1}, {0, 1, -4}, {2, -3, -2}, {7, 4, 1}.

4. {-1, 1, 1, 1}, {0, 2, 1, 1}, {1, 1, 1, 3}.

2. Преобразовать систему векторов

{1, -1, 1, 1}, {-1, 1, 1, 1}, {1, 1, 1, -1} в ортонормированную.

СИСТЕМА ВЕКТОРОВ

1.1.Разложение вектора по системе векторов

Векторk₁a₁ + k₂a₂ + … + k_na_nназывается линейной комбинацией векторов

a₁, a₂, … , a_nскоэффициентамиk₁, k₂, … , k_n .

Вектор bлинейно выражается через векторы a₁, a₂, … , a_n,если

b = k₁a₁ + k₂a₂ + … + k_na_n .

В этом случае говорят также, что bразлагается по векторам a₁, a₂, … , a_n. Каждый

n-мерный вектор b = { b₁, b₂, … , b_n } однозначно разлагается по диагональной системе

e₁ = {1, 0, … , 0},

e₂ = {0, 1, … , 0},

. . . . . . . . . . . . . .

e_n = {0, 0, … , 1}

с коэффициентами, которые равны координатам вектора b:

b = b₁e₁ + b₂e₂ + … + b_ne_n.

Чтобы найти разложение вектора b по системе векторов a₁, a₂, … , a_nдостаточно найти какое-нибудь решение системы уравнений

a₁x₁ + a₂x₂ + … + a_nx_n= b.

Пример.

Выяснить, разлагается ли вектор b по системе векторов a₁, a₂, … , a_n:

b = { 2, 7, 17 , 0}, a₁ = { 2, 4, 3 , 0}, a₂ = { –3, 0, 1 , 3}, a₃ = { 1, –1, 10, –3}.

Р е ш е н и е.Ищем общее решение системы уравнений

a₁x₁ + a₂x₂ + a₃ x₃= b

методомГаусса. Для этого запишем эту систему по координатам:

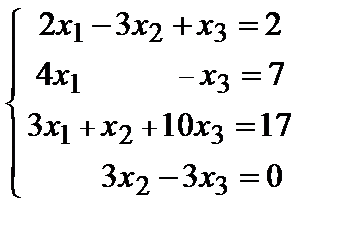
Расширенная матрица системы

~ ~

~ ~ ~ .

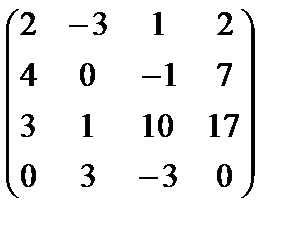
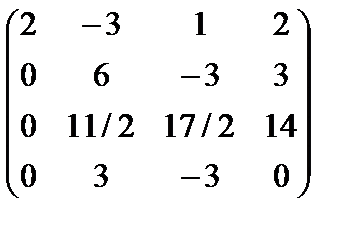
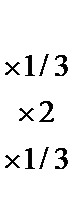
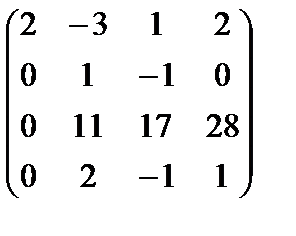
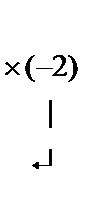
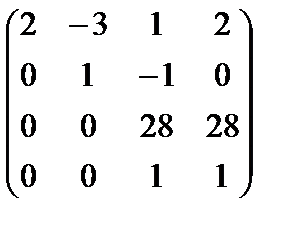
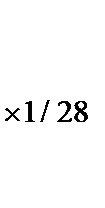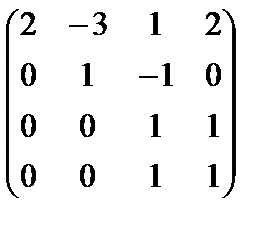
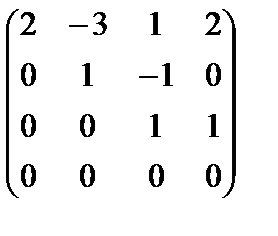Разрешенная система имеет вид: 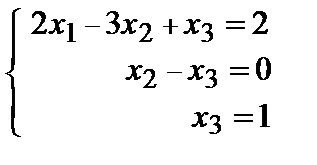(r_A = r_A|B = 3, n = 3).

Система определена: х₃ = 1, х₂ = 1, х₁ = 2.

Следовательно, b= 2a₁+ a₂+ a₃.

Задания.Выяснить, разлагается ли вектор b по системе векторов a₁, a₂, … , a_n :

1. b = { 2, 2, 3 , 3}, a₁ = { 1, 2, 3 , 1}, a₂ = { 2, 1, 2 , 3}, a₃ = { 3, 2, 4, 4}.

2. b = { 4, 1, 3 , 1}, a₁ = { 2, 0, 1 , 1}, a₂ = { 1, 1, 2 , -2}, a₃ = { 2, 1, 3, -3 }.

3. b = { -1, 1, 3 , 1}, a₁ = { 1, 2, 1 , 1}, a₂ = { 1, 1, 1 , 2}, a₃ = { -3, -2, 1, -3}.

4. b = { 1, 0, 0 , 1}, a₁ = { 2, 1, 1 , 3}, a₂ = { 3, 0, -1 , 2}, a₃ = { 1, -1, 0,1},

a₄ = { 1, 0, -2, -1 }.

5. Показать, что ни один из векторов диагональной системы не разлагается по остальным ее векторам.

6. Вектор b разлагается по системе векторов a₁, a₂, … , a_m . Доказать, что каждый вектор системы b+a₁, b+a₂, … , b+a_m разлагается по системе a₁, a₂, … , a_m .

1.2.Линейная зависимость

Система векторов a₁, a₂, … , a_nназывается линейно зависимой, если можно подобрать такие числа k₁, k₂, … , k_n , не все равные нулю, что

k₁a₁ + k₂a₂ + … + k_na_n = Θ, гдеΘ = {0, 0, … , 0}.

Система векторов a₁, a₂, … , a_nназывается линейно независимой, если из каждого соотношения вида k₁a₁ + k₂a₂ + … + k_na_n = Θследует

k₁=k₂= … =k_n=0.

Система векторов линейно зависима тогда и только тогда, когда система уравнений

a₁x₁ + a₂x₂ + … + a_nx_n= Θ

имеет ненулевое решение. Система векторов линейно н е зависима тогда и только тогда, когда система уравнений a₁x₁ + a₂x₂ + … + a_nx_n= Θимеет только нулевое решение.

Вектор b разлагается по линейно независимой системе a₁, a₂, … , a_n тогда и только тогда, когда a₁, a₂, … , a_n, b – линейно зависимая система векторов.

Система векторов линейно зависима, если количество координат у векторов системы меньше, чем векторов в системе.

Если каждый вектор системы b₁, b₂, … , b_n разлагается по векторам a₁, a₂, … , a_m и n>m, то b₁, b₂, … , b_n – линейно зависимая система векторов.

Пример 1.

Выяснить, является ли данная система векторов линейно зависимой или линейно независимой:

a₁ = { 3, 5, 1 , 4}, a₂ = { –2, 1, -5 , -7}, a₃ = { -1, –2, 0, –1}.

Р е ш е н и е.Ищем общее решение системы уравнений

a₁x₁ + a₂x₂ + a₃ x₃= Θ

методомГаусса. Для этого запишем эту однородную систему по координатам:

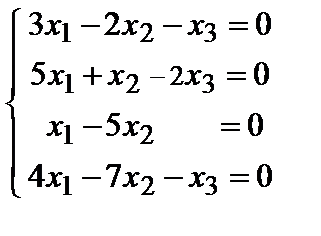
Матрица системы

~ ~ ~ .

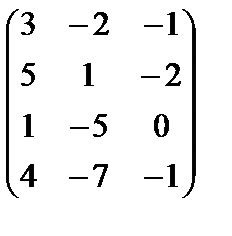
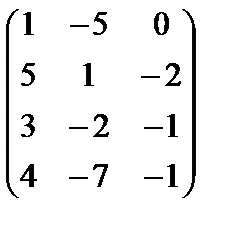
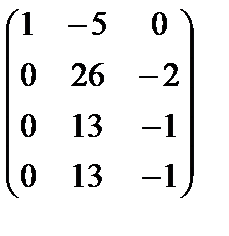
Разрешенная система имеет вид: 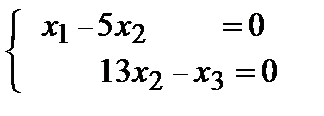(r_A = 2, n = 3). Система совместна и неопределена. Ее общее решение (x₂– свободная переменная ): x₃ = 13x₂;x₁=5x₂ =>

=>X_o = 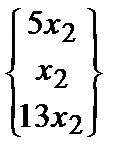.Наличие ненулевого частного решения, например, 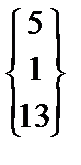, говорит о том, векторы a₁, a₂, a₃ линейно зависимы.

Пример 2.

Выяснить, является ли данная система векторов линейно зависимой или линейно независимой:

1. a₁ = { -20,-15, -4}, a₂ = { –7, -2, -4}, a₃ = { 3, –1, –2}.

Р е ш е н и е.Рассмотрим однородную систему уравнений a₁x₁ + a₂x₂ + a₃x₃ = Θ

или в развернутом виде (по координатам)

Система однородна. Если она невырождена, то она имеет единственное решение. В случае однородной системы – нулевое (тривиальное) решение. Значит, в этом случае система векторов независима. Если же система вырождена, то она имеет ненулевые решения и, следовательно, она зависима.

Проверяем систему на вырожденность:

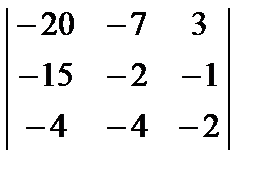= –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.

Система невырождена и ,т.о., векторы a₁, a₂, a₃ линейно независимы.

Задания.Выяснить,является ли данная система векторов линейно зависимой или линейно независимой:

1. a₁ = { -4, 2, 8}, a₂ = { 14, -7, -28}.

2. a₁ = { 2, -1, 3, 5}, a₂ = { 6, -3, 3, 15}.

3. a₁ = { -7, 5, 19}, a₂ = { -5, 7 , -7}, a₃ = { -8, 7, 14}.

4. a₁ = { 1, 8 , -1}, a₂ = { -2, 3, 3}, a₃ = { 4, -11, 9}.

5. a₁ = {0, 1, 1 , 0}, a₂ = {1, 1 , 3, 1}, a₃ = {1, 3, 5, 1}, a₄ = {0, 1, 1, -2}.

6. Доказать, что система векторов будет линейно зависимой, если она содержит:

а) два равных вектора;

б) два пропорциональных вектора.

7. Ненулевой вектор b разлагается по системе a₁, a₂, a₃ и по системе a₄, a₅, a₆. Доказать,

что a₁, a₂, a₃,a₄, a₅, a₆ линейно зависимая система векторов.

8. Доказать, что векторы a₂-a₁, a₃-a₁ не пропорциональны, если a₁, a₂, a₃– линейно

независимые векторы.

Базис и ранг системы векторов

Часть системы векторов называется базисом этой системы, если:

1) эта часть является линейно независимой системой векторов;

2) каждый вектор системы разлагается по векторам этой части.

Диагональная система векторов является базисом каждой системы, которая содержит ее в качестве части.

Если система уравнений

a₁x₁ + a₂x₂ + … + a_nx_n= Θ

является разрешенной, то векторы-коэффициенты при неизвестных, составляющих набор разрешенных неизвестных, образуют диагональную часть системы векторов a₁, a₂, … , a_n.

Векторы системы разлагаются по базису этой системы е д и н с т в е н н ы м образом.

Каждую линейно независимую часть системы векторов можно дополнить до базиса этой системы.

Все базисы данной системы состоят из одного и того же числа векторов.

Рангомсистемы векторов называется число векторов в любом ее базисе. Если ранг системы векторов равен r, то каждая линейно независимая часть этой системы, состоящая из rвекторов, является ее базисом. Системы векторов называются эквивалентными, если векторы одной системы разлагаются по векторам другой системы и наоборот. Ранги эквивалентных систем равны.

Вектор bтогда и только тогда разлагается по системе векторов a₁, a₂, … , a_m, когда ранги систем a₁, a₂, … , a_m и a₁, a₂, … , a_m, b равны.

Построение базиса системы векторовa₁, a₂, … , a_n и разложений векторов по базису:

1) Рассмотреть систему уравнений a₁x₁ + a₂x₂ + … + a_nx_n = Θи найти равносильную ей разрешенную систему уравнений

a´₁x₁ + a´₂x₂ + … + a´_nx_n = Θ.

2) Найти диагональную часть системы векторов a´₁, a´₂, … , a´_n.

3) Отметить векторы системы a₁, a₂, … , a_n, соответствующие диагональной части системы a´₁, a´₂, … , a´_n;они образуют базис системы a₁, a₂, … , a_n.

4) Разложить вектор a´_jпо диагональной части системы a´₁, a´₂, … , a´_n; вектор a_j, 1 ≤ j≤n, разлагается по базису, найденному в пункте 3, с коэффициентами разложения a´_jпо диагональной части системы a´₁, a´₂, … , a´_n.

Пример.

Найти базис системы векторов и векторы, не входящие в базис, разложить по базису:

а₁={5, 2, -3, 1}, а₂={4, 1, -2, 3}, а₃={1, 1, -1, -2}, а₄={3, 4, -1, 2}, а₅={13, 8, -7, 4}.

Р е ш е н и е. Рассмотрим однородную систему линейных уравнений

а₁х₁ +а₂х₂ +а₃х₃ +а₄х₄ +а₅х₅= 0

или в развернутом виде .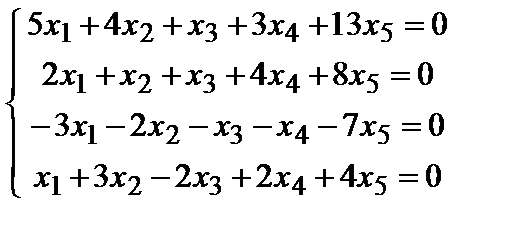

Будем решать эту систему методом Гаусса, не меняя местами строки и столбцы, и, кроме того, выбирая главный элемент не в верхнем левом углу, а по всей строке.Задача состоит в том, чтобы выделить диагональную часть преобразованной системы векторов.

~ ~

~ ~ ~ .

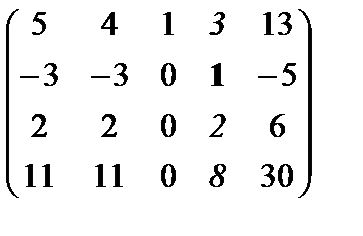
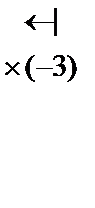
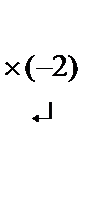
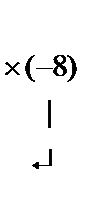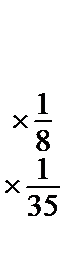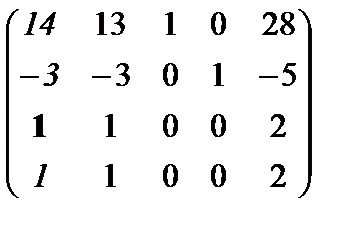
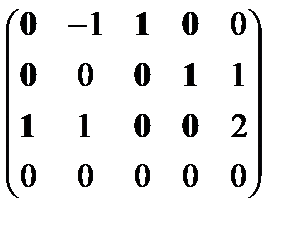Разрешенная система векторов, равносильная исходной, имеет вид

а₁¹х₁ +а₂¹х₂ +а₃¹х₃ +а₄¹х₄ +а₅¹х₅= 0,

где а₁¹= , а₂¹= , а₃¹= , а₄¹= 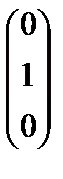, а₅¹= . (1)

Векторы а₁¹,а₃¹, а₄¹образуют диагональную систему. Следовательно, векторы а₁,а₃, а₄ образуют базис системы векторов а₁,а₂, а₃, а₄, а₅.

Разложим теперь векторы а₂иа₅ по базису а₁,а₃, а₄. Для этого сначала разложим соответствующие векторы а₂¹иа₅¹ по диагональной системеа₁¹,а₃¹, а₄¹, имея в виду, что коэффициентами разложения вектора по диагональной системе являются его координаты x_i.

Из (1) имеем:

а₂¹= а₃¹· (-1) + а₄¹· 0 + а₁¹·1 =>а₂¹= а₁¹ –а₃¹.

а₅¹= а₃¹· 0 + а₄¹· 1 + а₁¹·2 =>а₅¹= 2а₁¹ +а₄¹.

Векторы а₂иа₅ разлагаются по базису а₁,а₃, а₄ с теми же коэффициентами, что и векторы а₂¹иа₅¹ по диагональной системе а₁¹,а₃¹, а₄¹ (те коэффициенты x_i). Следовательно,

а₂= а₁ –а₃, а₅= 2а₁ +а₄.

Задания. 1.Найти базис системы векторов и векторы, не входящие в базис, разложить по базису:

1. a₁ = { 1, 2, 1}, a₂ = { 2, 1, 3}, a₃ = { 1, 5, 0 }, a₄ = { 2, -2, 4}.

2. a₁ = { 1, 1, 2}, a₂ = { 0, 1, 2}, a₃ = { 2, 1, -4 }, a₄ = { 1, 1, 0}.

3. a₁ = { 1, -2, 3}, a₂ = { 0,1, -1}, a₃ = { 1, 3, 0}, a₄ = { 0, -7, 3 }, a₅ = { 1, 1, 1}.

4. a₁ = { 1, 2, -2}, a₂ = { 0, -1, 4}, a₃ = { 2, -3,3 }.

2.Найти все базисы системы векторов:

1. a₁ = { 1, 1, 2}, a₂ = { 3, 1, 2}, a₃ = { 1, 2, 1 }, a₄ = { 2, 1, 2}.

2. a₁ = { 1, 1, 1}, a

Наши рекомендации